Backtracking & Dynamic Programming in Data Structure

What is backtracking?

Backtracking uses a brute-force technique to obtain the required result. Backtracking implies that if the current solution is ineffective, one should go back and attempt another. It is used to solve an issue with several solutions. A space state tree is a tree that displays all of the possible issue states, from the root as the starting state to the leaf as the final state.

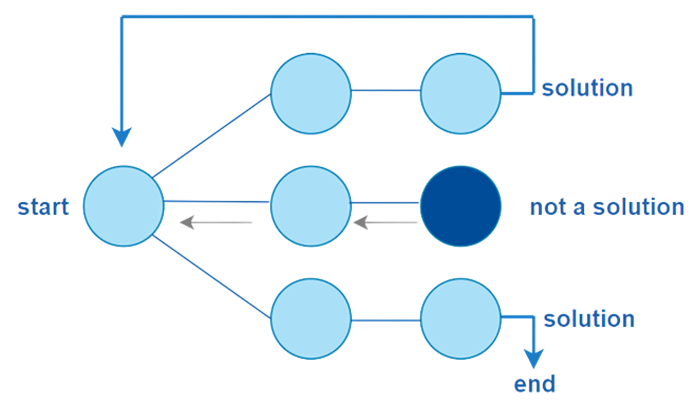
Usages of Backtracking

• Hamiltonian Path
• N Queen Problem
• Maze Solving Problems
• Knight's Tour Problem

Basic Terminologies of Backtracking

• Candidate: A candidate is a possible option or component that can be added to the current solution.
• Solution: The solution is a legitimate and complete configuration that meets all of the problem's restrictions.
• Partial Solution: A partial solution is an intermediate or incomplete configuration created during the backtracking process.
• Decision Space: The decision space is the collection of all potential candidates or options at each decision point.
• Decision Point: A decision point is a phase in the algorithm where a candidate is selected and added to the partial solution.
• Feasible Solution: A feasible option is partial or complete and satisfies all restrictions.
• Dead End: A dead end is when a partial solution cannot be expanded without breaching limitations.
• Backtrack: Backtracking entails undoing earlier decisions and returning to the original decision point.
• Search Space: The search space covers all potential candidate and option combinations.
• Optimal Solution: The best potential solution to an optimization problem.

Different types of backtracking problems

Backtracking problems are divided into three categories:

• Decision Problems: Here, we look for a feasible solution.
• Optimization Problems: For this class, we seek the best solution.
• Enumeration issues: We identify a set of all conceivable solutions to issues of this type.

Backtracking's Complexity

Backtracking performs poorly in terms of time complexity because it is essentially brute force. Backtracking can be seen with the following time complexities:

• Exponential O(K^N)
• Factorial (O(N!)

Applications of Backtracking

• Developing smart bots to play board games like chess.
• Solve mazes and puzzles, such as the N-Queen problem.
• Network Routing and Congestion Control.
• Decryption
• Text Justification

Brute Force Approach

A Brute Force approach is a clear and straightforward method of problem-solving in which all feasible solutions to a given problem are listed. Attackers or hackers use the brute force strategy to try multiple combinations to break any website or system.

Dynamic Programming

Dynamic programming is a strategy for solving a problem by breaking it down into a collection of sub-problems, solving each sub-issue only once, and keeping the solution in memory. When the identical problem happens again, the previously stored solution from memory is returned. T

Dynamic Programming Usages

• Sequence alignment, Documenting different algorithms, Plagiarism detection
• Duckworth Lewis Method in Cricket, Flight Control
• Speech recognition, Image processing, Machine Learning Algorithms
• Financial Trading, Bioinformatics, and Operations Research

Dynamic Programming Approaches

• Top-Down Approach (Memoization)
• Bottom-Up Approach (Tabulation)

Top-Down Approach (Memoization)

• Implement the solution naturally using recursion, but change it to save the solution to each subproblem in an array or hash table. 
• This method initially determines whether it has already solved the subproblem.
• If so, it returns the saved value and saves any subsequent calculations.
• Otherwise, the top-down technique will calculate subproblem solutions in the usual way. 
• A memoized form of a recursive solution remembers the prior results.

Bottom-Up Approach (Tabulation)

• A top-down technique taken in reverse, but iteratively.
• Depends on a natural concept: the answer to any subproblem is determined solely by the resolution of smaller subproblems.
• Solves them iteratively from smallest to largest and stores the results in extra memory. 

Problems of Dynamic Programming 

• Issues with climbing stairs
• The minimum coin change
• The maximum subarray sum
• The longest common subsequence
• The minimum amount of jumps