Recursion in C: Types, its Working and Examples

What is Recursion in C?

Recursion in C programming allows a function to call itself to solve an issue. It entails decomposing a challenging issue into more manageable issues and then solving each one again. In this C tutorial, we'll delve into recursive functions, types of recursion, and the advantages and disadvantages of recursion. To go a little deeper, consider our Online C Programming Course With Certificate Free.

Recursive Function in C

Recursive functions in the C programming language offer a fascinating yet complex paradigm of problem-solving. In this paradigm, a function repeatedly calls itself until a specified condition is met.

• Through their intricate design and repetitive nature, these functions stand out as elegant solutions to challenges that require multiple steps or processes to be completed.
• In simple terms, recursive functions in C harness the power of iteration leading to efficient, compact, and concise code for tasks such as computing the factorial of a number, traversing tree data structures, and implementing the Fibonacci Sequence.

Mastering the recursive function concept can unlock substantial potential for any programmer, providing them with the foundational skills to tackle a diverse array of computational problems with both clarity and precision.

Example of recursion program in C

#include<stdio.h> 
int fibonacci(int); 
void main () 
{ 
 int n,f; 
 n = 12; 
 f = fibonacci(n); 
 printf("%d",f); 
} 
int fibonacci (int n) 
{ 
 if (n==0) 
 { 
 return 0; 
 } 
 else if (n == 1) 
 { 
 return 1; 
 } 
 else 
 { 
 return fibonacci(n-1)+fibonacci(n-2); 
 } 
} 

This C program in the C Online Compiler uses recursion to determine the nth Fibonacci number. It accepts the input "n" and returns 0 or 1 depending on whether "n" is 0 or 1. Otherwise, it adds the two Fibonacci numbers before calculating the Fibonacci number recursively. The result is displayed in the main function after the Fibonacci number for 'n' has been calculated.

Output

144

Read More - Top 50 Mostly Asked C Interview Questions and Answers

Types of Recursion in C

The following are the different types of recursion in C programming language:

1. Direct Recursion
2. Indirect Recursion
3. Tail Recursion
4. No Tail/ Head Recursion
5. Linear recursion
6. Tree Recursion

1. Direct Recursion

A function calls itself within the definition of the function through direct recursion. It is a simple and typical type of recursion in C. The size of the problem normally decreases with each recursive iteration until a base case is reached to end the recursion.

Direct Recursion Example

#include <stdio.h>
void directRecursion(int n) {
if (n > 0) {
printf("%d ", n);
 directRecursion(n - 1); // Recursive call
 }
}
int main() {
int num = 5;
printf("Direct Recursion: ");
directRecursion(num);
return 0;
}

This C code shows direct recursion by repeatedly invoking the directRecursion function with decreasing values of 'n' until 'n' equals 0. The output reads "Direct Recursion: 5 4 3 2 1," listing n's values in decreasing order starting at 5.

Output

Direct Recursion: 5 4 3 2 1

2. Indirect Recursion

At least two functions that call each other repeatedly in a cycle constitute indirect recursion. By transferring control back and forth between each other until a termination condition is satisfied, these functions cooperate to solve a problem. Even though it is less common, this kind of recursion has its uses.

Indirect Recursion Example

#include <stdio.h>
void functionB(int n);
void functionA(int n) {
if (n > 0) {
 printf("%d ", n);
 functionB(n - 1); // Indirect recursive call
 }
}
void functionB(int n) {
 if (n > 0) {
 printf("%d ", n);
 functionA(n / 2); // Indirect recursive call
 }
}
int main() {
 int num = 5;
 printf("Indirect Recursion: ");
 functionA(num);
 return 0;
}

Two functions, functionA & functionB, are called indirectly by recursive calls in this example of indirect recursion in C Playground. FunctionA prints 'n' values in decreasing order and calls functionB, which then prints 'n' values and calls functionA with 'n/2'. Up until the recursion ends, this pattern persists. The code outputs a series of integers when you execute it with num set to 5, "5 4 2 1."

Output

Indirect Recursion: 5 4 2 1

3. Tail Recursion

When a recursive function calls itself in a loop and that looping statement is the final one the function performs, the function is said to be "tail-recursive." There are no more functions or statements that can call the recursive function after that.

Tail Recursion Example

#include <stdio.h>
void tailRecursion(int n, int accumulator) {
 if (n == 0) {
 printf("Result: %d\n", accumulator);
 return;
 }
 tailRecursion(n - 1, accumulator + n); // Tail recursive call
}
int main() {
 int num = 5;
 printf("Tail Recursion:\n");
 tailRecursion(num, 0);
 return 0;}

This C program shows the use of tail recursion to compute the sum of all numbers from 'n' down to 1. When 'n' is set to 5, it optimizes the recursion for tail-call optimization, outputting the outcome as "Result: 15".

Output

Tail Recursion:
Result: 15

4. Non-Tail / Head Recursion

The non-tail or head recursion of a function The initial statement in a function will be the recursive call if it does one on its own. It implies that no statement or operation should be called prior to the recursive calls. Additionally, when a recursive call is made, the head recursive accomplishes nothing. Instead, every action is finished at the return time.

Head Recursion Example

#include <stdio.h>
void noTailRecursion(int n) {
 if (n > 0) {
 noTailRecursion(n - 1); // Recursive call
 printf("%d ", n);
 noTailRecursion(n - 2); // Another recursive call
 }
}
int main() {
 int num = 5;
 printf("Non-Tail/Head Recursion: ");
 noTailRecursion(num);
 return 0;}

The function noTailRecursion calls itself recursively before and after printing a number in this example of non-tail (or non-head) recursion in C. It produces the complex, non-linear output pattern "No Tail/Head Recursion: 1 2 3 4 5 3 1 2 3 4 5 3 1..." when run with num set to 5.

Output

Non-Tail/Head Recursion: 1 2 1 3 1 2 4 1 2 1 3 5 1 2 1 3 1 2

5. Linear Recursion

If a function only makes one call to itself each time it is executed and expands linearly as a function of the size of the problem, the function is said to be linear recursive.

Linear Recursion Example

#include <stdio.h>
int linearRecursion(int n) {
 if (n == 0) {
 return 0;
 } else {
 return n + linearRecursion(n - 1); // Linear recursive call
 }
}
int main() {
 int num = 5;
 printf("Linear Recursion: Sum of 1 to %d is %d\n", num, linearRecursion(num));
 return 0;}

This C program in the C Editor calculates the sum of all the numbers from 1 to 'n' as an example of linear recursion. It employs a simple linear recursive call, and when run with the value of 'num' set to 5, it displays the following message: "Linear Recursion: Sum of 1 to 5 is 15."

Output

Linear Recursion: Sum of 1 to 5 is 15

6. Tree Recursion

When a recursive function in C calls itself more than once, the result is a branching structure that resembles a tree. This is known as "tree recursion." Recursive calls are frequently employed to solve issues involving hierarchical or connected data structures because each call can result in other calls. For issues with numerous recursive subproblems, this kind of recursion is especially helpful.

Tree Recursion Example

#include <stdio.h>
void treeRecursion(int n) {
 if (n > 0) {
 printf("%d ", n);
 treeRecursion(n - 1); // Recursive call 1
 treeRecursion(n - 1); // Recursive call 2
 }
}
int main() {
 int num = 3;
 printf("Tree Recursion: ");
 treeRecursion(num);
 return 0;}

In this C code, a function named treeRecursion executes two recursive calls with decreasing values of 'n' in a branching pattern to demonstrate tree recursion. It prints a tree-like structure of integers when 'num' is set to 3 when executed: "Tree Recursion: 3 2 1 1 2 1 2 1."

Output

Tree Recursion: 3 2 1 1 2 1 1 2 1

Pseudocode in C

Informally describing the logic of a program or algorithm without following the exact syntax of a certain programming language is known as pseudocoding. Here is some sample pseudocode in C for recursive functions.

function recursiveFunction(parameter):
if (base_test):
return given_value;
else if (another_base_test):
return other_given_value;
else:
// Add a statement here;
return recursiveFunction(parameter); // Recursive call

This pseudocode defines the recursive function, which uses base_test and another_base_test to handle base cases and returns data appropriately. It contains a placeholder statement that executes a recursive call with the same parameter if neither base case is met.

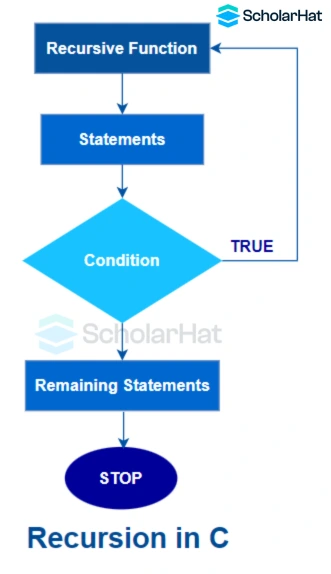
How Recursion Works?

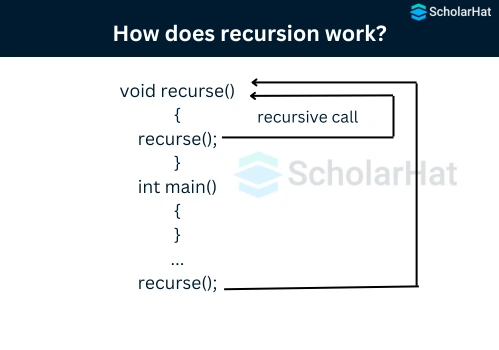
• Tasks are broken down into subtasks using recursive functions in C.
• Termination conditions are a feature of subtasks; they put a stop to the recursion.
• Recursion is infinite if the prerequisites for termination are not satisfied.
• When a base case is found, recursion comes to an end; the base case does not call itself.
• Both base cases (non-recursive) & recursive cases (self-calling) exist for recursive functions.

Example

#include <stdio.h>
// Recursive function to calculate the sum of integers from 1 to n
int sum(int n) {
// Base case: If n is 1, return 1
if (n == 1) {
return 1;
} else {
 // Recursive case: Add n to the sum of integers from 1 to (n-1)
 return n + sum(n - 1);
 }
}
int main() {
 int num=5;
if (num <= 0) {
printf("The number is not a positive number\n");
 } else {
 int result = sum(num);
 printf("The sum of integers from 1 to %d is %d\n", num, result);
}
 return 0;

This C program in the C Online Compiler utilizes recursion to determine the total of all integers from 1 to n. It offers a user interface for entering n, checks that it is positive, and then computes and shows the sum.

Output

The sum of integers from 1 to 5 is 15

Advantages and Disadvantages of Recursion in C

The advantages of recursion are as follows:

• Writing code may be simpler.
• To resolve issues like the Hanoi Tower that are inherently recursive.
• Lessen the frequency of pointless function calls.
• Exceptionally practical when using the same solution.
• Recursion cuts down on code length.
• It helps a lot in resolving the data structure issue.
• Evaluations of infix, prefix, and postfix stacks, among other things.

The disadvantages of recursion are as follows:

• In general, recursive functions are slower than non-recursive ones.
• To store intermediate results on the system stacks, a significant amount of memory may be needed.
• The code is difficult to decipher or comprehend.
• It is not more effective in terms of complexity over time and space.
• If the recursive calls are not adequately checked, the machine can run out of memory.

Summary

Recursion is a very useful approach when it comes to programming. It has wide applications ranging from calculating the factorial of a number to sorting and traversal algorithms. If you want to learn such an important concept in more depth, just consider our C Certification Program. It will prove a practical booster in your journey of programming.