Start Learning Free
Previous Tutorial
22
DecHow to Implement Fibonacci Series in C#
19 Sep 2024
Beginner
1.14K Views
17 min read
Learn with an interactive course and practical hands-on labs
Best Free C# Course: Learn C# In 21 Days
Fibonacci Series
The Fibonacci series is a sequence of integers in which each number is the sum of the two numbers before it, beginning with 0 and 1. It is a fundamental topic in mathematics and programming, frequently used to explain recursion and dynamic programming ideas.
In this C# tutorial, I will tell you all about the Fibonacci Series using C#, so that if you are preparing for an exam or interview you can easily explain it. We will also discuss two basic approaches to implementing the Fibonacci series in C# such as iterative and recursive methods.
What is the Fibonacci Series?
The following is a Fibonacci sequence :
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34... |
Each number in the series is obtained by adding the two numbers preceding it. The Fibonacci series is just a sequence of numbers in the following order.
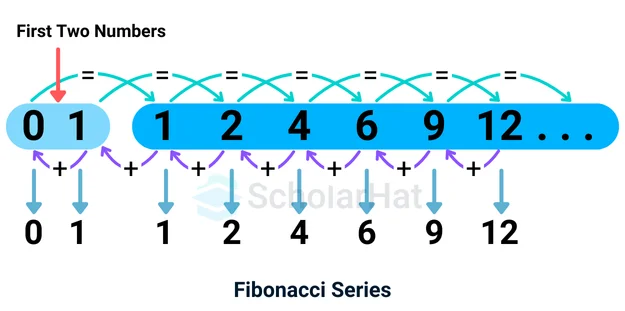
The mathematical definition of the Fibonacci sequence is
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) for n > 1
What are the different ways to implement Fibonacci in C#?
In C#, we have two options for printing the Fibonacci series. They are as follows.
- Iterative Approach
- Recursion Approach
Method 1: Iterative approach.
The iterative approach is efficient and easy to implement. It avoids the overhead of recursive function calls and is typically faster for longer sequences.
This is how it works.
- Initialize the initial two Fibonacci numbers, 0 and 1.
- Loop over the series and add the final two integers to find the next Fibonacci number.
- Save and print the calculated Fibonacci numbers.
- Let's implement it actually with C# Compiler.
Example
using System;
public class Program
{
public static void Main(string[] args)
{
int n = 10; // Number of Fibonacci terms to generate
int first = 0, second = 1, next;
Console.WriteLine("Fibonacci Series (Iterative Method):");
Console.Write(first + " " + second + " ");
for (int i = 2; i < n; i++)
{
next = first + second;
Console.Write(next + " ");
first = second;
second = next;
}
}
}
Output
Fibonacci Series (Iterative Method):
0 1 1 2 3 5 8 13 21 34
Explanation
Advantages
Method 2: Recursive Approach.
The recursive technique is similar to the mathematical definition of Fibonacci numbers, in that each phrase is defined using the two terms that came before it. This method, however, is inefficient for big n because it requires repeated function calls.Example
using System;
public class Program
{
public static void Main(string[] args)
{
int n = 10; // Number of Fibonacci terms to generate
Console.WriteLine("Fibonacci Series (Recursive Method):");
for (int i = 0; i < n; i++)
{
Console.Write(Fibonacci(i) + " ");
}
}
public static int Fibonacci(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
}
Output
Fibonacci Series (Recursive Method):
0 1 1 2 3 5 8 13 21 34
Explanation
Advantages
Disadvantages
Which Method Should You Use?
1. For smaller values of n: The recursive approach is simple and straightforward to implement. However, when n grows, it becomes increasingly inefficient owing to duplicate calculations.2. For large values of n: The iterative technique is preferred. It works in linear time and is substantially more efficient at calculating huge Fibonacci numbers.
Optimizing the Recursive Approach via Memorization
One of the main disadvantages of recursion is its inefficiency owing to repeated calculations. Memoization is a prominent approach to overcoming this. By saving previously computed Fibonacci numbers, we avoid unnecessary calculations, significantly boosting the performance of the recursive solution.
Example with Memoization
using System;
using System.Collections.Generic;
public class Program
{
private static Dictionary memo = new Dictionary();
public static void Main(string[] args)
{
int n = 10;
Console.WriteLine("Fibonacci Series (Recursive with Memoization):");
for (int i = 0; i < n; i++)
{
Console.Write(Fibonacci(i) + " ");
}
}
public static int Fibonacci(int n)
{
if (memo.ContainsKey(n))
return memo[n];
if (n == 0)
return 0;
if (n == 1)
return 1;
int result = Fibonacci(n - 1) + Fibonacci(n - 2);
memo[n] = result;
return result;
}
}
Output
Fibonacci Series (Recursive with Memoization):
0 1 1 2 3 5 8 13 21 34
Advantages of memorization
Improved efficiency: Storing computed values reduces the temporal complexity to O(n). Avoid Redundant Computation: Each Fibonacci number is calculated once.How to find the nth Fibonacci number in the Fibonacci Series in C#?
In addition, the nth Fibonacci number from the Fibonacci series can be printed in C#. The following example prints the nth integer in the Fibonacci sequence.1. Using Recursion
using System;
public class Program
{
// Recursive method to find nth Fibonacci number
public static int Fibonacci(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
public static void Main(string[] args)
{
int n = Convert.ToInt32(Console.ReadLine());
int result = Fibonacci(n);
Console.WriteLine($"The {n}th Fibonacci number is: {result}");
}
}
Output
12
The 12th Fibonacci number is: 144
Explanation
2. Without Using a Recursive Function
In this example, we will write an iterative program to discover the nth Fibonacci number (without recursion). The iterative method is more efficient and eliminates the overhead of recursive calls. using System;
public class Program
{
public static void Main(string[] args)
{
// Ask user for the position of Fibonacci number
int n = Convert.ToInt32(Console.ReadLine());
// Check if input is valid
if (n < 0)
{
Console.WriteLine("Please enter a positive integer.");
}
else
{
int result = FindFibonacci(n);
Console.WriteLine($"The Fibonacci number at position {n} is: {result}");
}
}
// Method to find nth Fibonacci number without recursion
public static int FindFibonacci(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
int first = 0, second = 1, next = 0;
// Iteratively calculate Fibonacci numbers
for (int i = 2; i <= n; i++)
{
next = first + second;
first = second;
second = next;
}
return next;
}
}
Output
12
The Fibonacci number at position 12 is: 144
Explanation
How to Print the Fibonacci Series up to a given number in C#?
Now we'll look at how to print the Fibonacci sequence up to a certain integer in C#. Please look at the following program. using System;
namespace LogicalPrograms
{
public class Program
{
static void Main(string[] args)
{
int firstNumber = 0, SecondNumber = 1, nextNumber, number;
Console.Write("Fibonacci series upto given number : ");
number = int.Parse(Console.ReadLine());
//First print first and second number
Console.Write(firstNumber + " " + SecondNumber + " ");
nextNumber = firstNumber + SecondNumber;
//Starts the loop from 2 because 0 and 1 are already printed
for (int i = 2; nextNumber < number; i++)
{
Console.Write(nextNumber + " ");
firstNumber = SecondNumber;
SecondNumber = nextNumber;
nextNumber = firstNumber + SecondNumber;
}
Console.ReadKey();
}
}
}
Output
100
Fibonacci series upto given number : 0 1 1 2 3 5 8 13 21 34 55 89
Summary
By studying and applying Fibonacci in these various methods, you will not only increase your comprehension of core programming ideas but also your C# problem-solving skills. Whether you're preparing for coding interviews or developing mission-critical systems, learning both ways can help you code more efficiently. Also, Consider our C# Programming Course for a better understanding of all C# concepts.FAQs
A Fibonacci series program in C# is a code implementation that generates the Fibonacci sequence, where each number is the sum of the two preceding ones, starting from 0 and 1.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.
In the Fibonacci sequence of numbers, each number in the sequence is the sum of the two numbers before it, with 0 and 1 as the first two numbers.
Take our Csharp skill challenge to evaluate yourself!
In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.