Binary Tree Array Implementation

A Binary Tree Array Implementation is a way of representing a binary tree using a linear array instead of pointers (links). In this method, nodes are stored in sequential indices of an array, and the parent–child relationship is determined using simple mathematical formulas rather than explicit pointers.

In this Data Structure tutorial, you will be able to learn about what is binary tree, why use an array for binary tree implementation, how to implement binary tree using array in C++ with full code breakdown and explanation, advantages, disadvantages and real world applications of binary tree array implementation. Build your coding foundation in just 21 days with our Free DSA Course and earn a  certificate.

What is Binary Tree?

A binary tree is a hierarchical data structure consisting of nodes, where each node has at most two children, usually referred to as the left child and the right child. The topmost node is called the root, and nodes without children are leaves.

Traditionally, binary trees are implemented using linked nodes, where each node contains data and pointers to its children. However, another widely used approach is array implementation, where the binary tree is represented as a linear array structure.

Why Use an Array for Binary Tree Implementation?

Key reasons to choose arrays:

• Memory Efficiency: There is no pointer overhead means arrays use less space per node.
• Cache Friendliness: Accessing contiguous memory improves performance due to better cache usage.
• Simpler Indexing: You can access child and parent nodes with simple math operations.
• Ease in Complete Trees: This method is great for balanced or complete trees because it avoids wasting space.

When to Use Array Implementation?

• When working with complete binary trees or heap-based algorithms.
• When fast parent/child access is needed without pointer overhead.
• When memory fragmentation must be avoided.

How Array Representation Works?

• Root Node: Placed at index 0 (or 1 if using 1-based indexing).
• Left Child: For a node at index i, the left child is at 2i + 1.
• Right Child: For a node at index i, the right child is at 2i + 2.
• Parent Node: For a node at index i, the parent is at (i – 1) / 2.

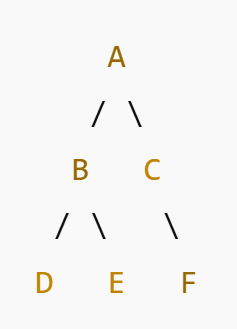
Example

• Node A (index 0) → left child = B (index 1), right child = C (index 2).
• Node B (index 1) → left child = D (index 3), right child = E (index 4).
• Node C (index 2) → left child = F (index 5).

Implementing a Binary Tree in an Array

The code implements a binary tree using a dynamic array instead of the traditional pointer-based node structure. It’s designed for a complete binary tree, where nodes are stored in level-order (breadth-first) sequence, and indices are used to navigate parent-child relationships. The implementation includes methods for:

• Initializing the tree.
• Inserting nodes (general and specific left/right child insertion).
• Traversing the tree (level-order and in-order).
• Searching for a value.
• Deleting the root (with a note for heap-like behavior).

The main function demonstrates the usage by building a small tree and performing operations.

<#include <iostream> 
<#include <vector> 
<#include <stdexcept> 

class ArrayBinaryTree { 
private: 
    std::vector<int> tree; // Dynamic array to store nodes 
    size_t size;           // Current number of nodes 
    size_t capacity;       // Total capacity of the array 

    void resize() { 
        if (size == capacity) { 
            capacity *= 2; 
            tree.resize(capacity, 0); // Initialize new slots with 0 (or use INT_MIN for sentinel) 
        } 
    } 

public: 
    ArrayBinaryTree(size_t initial_capacity = 10) : size(0), capacity(initial_capacity) { 
        tree.resize(initial_capacity, 0); // Initialize with zeros 
    } 

    size_t get_left_child_index(size_t index) const { 
        return 2 * index + 1; 
    } 

    size_t get_right_child_index(size_t index) const { 
        return 2 * index + 2; 
    } 

    size_t get_parent_index(size_t index) const { 
        if (index == 0) return static_cast<size_t>(-1); // No parent for root 
        return (index - 1) / 2; 
    } 

    void insert(int data) { 
        resize(); 
        tree[size] = data; 
        size++; 
    } 
    void insert_left(size_t parent_index, int data) { 
        size_t left_index = get_left_child_index(parent_index); 
        if (left_index >= capacity) { 
            resize(); 
        } 
        if (tree[left_index] != 0) { 
            throw std::runtime_error("Left child already exists"); 
        } 
        tree[left_index] = data; 
        size++; 
    } 
    void insert_right(size_t parent_index, int data) { 
        size_t right_index = get_right_child_index(parent_index); 
        if (right_index >= capacity) { 
            resize(); 
        } 
        if (tree[right_index] != 0) { 
            throw std::runtime_error("Right child already exists"); 
        } 
        tree[right_index] = data; 
        size++; 
    } 
    void level_order_traversal() const { 
        std::cout << "Level Order: "; 
        for (size_t i = 0; i < size; ++i) { 
            if (tree[i] != 0) { 
                std::cout << tree[i] << " "; 
            } 
        } 
        std::cout << std::endl; 
    } 
    void in_order_traversal(size_t index, std::vector<int>& result) const { 
        if (index >= size || tree[index] == 0) { 
            return; 
        } 
        in_order_traversal(get_left_child_index(index), result); 
        result.push_back(tree[index]); 
        in_order_traversal(get_right_child_index(index), result); 
    } 

    std::vector<int> in_order_traversal() const { 
        std::vector<int> result; 
        in_order_traversal(0, result); 
        return result; 
    } 
    int search(int data) const { 
        for (size_t i = 0; i < size; ++i) { 
            if (tree[i] == data) { 
                return static_cast<int>(i); 
            } 
        } 
        return -1; // Not found 
    } 
    // Example deletion for root (heap-like, for complete trees) 
    void delete_root() { 
        if (size == 0) return; 
        tree[0] = tree[size - 1]; 
        tree[size - 1] = 0; 
        size--; 
        // Note: For heaps, add heapify_down here 
    } 
}; 
int main() { 
    ArrayBinaryTree bt; 
    bt.insert(1); // Root 
    bt.insert(2); // Left of root 
    bt.insert(3); // Right of root 
    bt.insert(4); // Left of 2 
    bt.insert(5); // Right of 2 

    bt.level_order_traversal(); // Expected: 1 2 3 4 5 

    std::vector<int> in_order = bt.in_order_traversal(); 
    std::cout << "In Order: "; 
    for (int val : in_order) { 
        std::cout << val << " "; 
    } 
    std::cout << std::endl; // Expected: 4 2 5 1 3 

    int search_result = bt.search(3); 
    std::cout << "Index of 3: " << search_result << std::endl; // Expected: 2 

    return 0; 
} 

Code Breakdown and Explanation

1. Header Files and Class Definition

<#include <iostream> 
<#include <vector> 
<#include <stdexcept> 
class ArrayBinaryTree { 
private: 
    std::vector<int> tree; // Dynamic array to store nodes 
    size_t size;           // Current number of nodes 
    size_t capacity;       // Total capacity of the array

Headers:

• <iostream>:For input/output operations (e.g., printing traversal results).
• <vector> : For the dynamic array (std::vector) to store the tree.
• <stdexcept>: For throwing exceptions (e.g., when inserting into an occupied position).

Class Members:

• tree: A std::vector<int>to store the nodes. Using int simplifies the example, but you could template it for generic types.
• size: Tracks the number of nodes currently in the tree.
• capacity: Tracks the total allocated size of the vector, used for resizing logic.

2. Private Utility Method: resize

void resize() {
    if (size == capacity) {
        capacity *= 2;
        tree.resize(capacity, 0); // Initialize new slots with 0 (or use INT_MIN for sentinel)
    }
}

• Checks if size equals capacity (i.e., the vector is full).
• Doubles capacity and resizes the vector using tree.resize(capacity, 0), filling new slots with 0 (a sentinel value indicating an empty slot).

3. Constructor

ArrayBinaryTree(size_t initial_capacity = 10) : size(0), capacity(initial_capacity) {
    tree.resize(initial_capacity, 0); // Initialize with zeros
}

• Sets size to 0 (no nodes yet).
• Sets capacity to initial_capacity.
• Initializes tree with initial_capacity slots, all set to 0.

4. Index Calculation Methods

These methods compute indices for navigating the tree, assuming 0-based indexing.

size_t get_left_child_index(size_t index) const {  
    return 2 * index + 1;  
}  

size_t get_right_child_index(size_t index) const {  
    return 2 * index + 2;  
}  

size_t get_parent_index(size_t index) const {  
    if (index == 0) return static_cast<size_t>(-1); // No parent for root  
    return (index - 1) / 2;  
}  

• Left Child: For a node at index i, the left child is at 2*i + 1.
• Right Child: The right child is at 2*i + 2.
• Parent: For a node at index i (except root), the parent is at (i-1)/2. The root (index 0) has no parent, so -1 is returned.

Basic Operations

5. Insertion Methods

General Insertion

void insert(int data) {
    resize();
    tree[size] = data;
    size++;
}

• Calls resize() to ensure enough space.
• Places data at index size (end of current tree).
• Increments size.

Use Case: Ideal for building complete binary trees or heaps.

6. Traversal Methods

Level-Order Traversal

void level_order_traversal() const {  
    std::cout << "Level Order: ";  
    for (size_t i = 0; i < size; ++i) {  
        if (tree[i] != 0) {  
            std::cout << tree[i] << " ";  
        }  
    }  
    std::cout << std::endl;  
}  

• Iterates through the first size elements of tree. Prints non-zero values (skipping empty slots).

Array storage inherently follows level-order, making this traversal O(n) and straightforward.

void in_order_traversal(size_t index, std::vector<int>& result) const {  
    if (index >= size || tree[index] == 0) {  
        return;  
    }  
    in_order_traversal(get_left_child_index(index), result);  
    result.push_back(tree[index]);  
    in_order_traversal(get_right_child_index(index), result);  
}  

std::vector<int> in_order_traversal() const {  
    std::vector<int> result;  
    in_order_traversal(0, result);  
    return result;  
}  

• Stops if index is out of bounds or the node is empty (tree[index] == 0).
• Recursively processes the left subtree. Adds the current node’s value to result.
• Recursively processes the right subtree. The public method initializes an empty result vector and starts recursion from the root (index 0).

Use Case: In-order traversal is useful for binary search trees (to get sorted order) or general tree processing.

7. Search Method

int search(int data) const {
    for (size_t i = 0; i < size; ++i) {
        if (tree[i] == data) {
            return static_cast<int>(i);
        }
    }
    return -1; // Not found
}

• Iterates through the first size elements.
• Returns the index if data is found, else -1.

Limitation: Linear search (O(n)). For binary search trees, you’d optimize by following BST properties, but this implementation assumes a general binary tree.

Deletion Method (Root)

void delete_root() {
    if (size == 0) return;
    tree[0] = tree[size - 1];
    tree[size - 1] = 0;
    size--;
    // Note: For heaps, add heapify_down here
}

• If size is 0, does nothing.
• Copies the last node (tree[size-1]) to the root (tree[0]).
• Clears the last slot (tree[size-1] = 0).
• Decrements size.

Note: The comment about heapify_down indicates this is a starting point for heap deletion. For general trees, deletion is complex and may require restructuring.

Advantages of Array Implementation

• Space Savings: No need for pointers, each node only stores its data.
• Fast Access: Parent and child nodes can be accessed in constant time O(1) using simple arithmetic formulas.
• Efficient for Heaps: Binary heaps (min-heap, max-heap) are almost always array-based due to performance benefits.
• Easy Serialization: Arrays can be directly serialized/deserialized, simplifying storage and transmission.

Disadvantages of Array Implementation

• Wasted Space: For skewed trees, many indices remain unused (e.g., a right-skewed tree may require exponentially more space).
• Fixed Size Limitations: Static arrays have limited capacity and resizing requires O(n) time.
• Complex Deletions: Maintaining the "completeness" property after deletions is difficult without restructuring.
• Not Suitable for Sparse Trees: Linked representations handle sparse or irregular structures more efficiently than arrays.

Real-World Applications

1. Binary Heaps: Foundation of priority queues, heap sort, and algorithms like Dijkstra’s shortest path.
2. Segment Trees and Fenwick Trees (BITs) : Widely used in range queries and updates in competitive programming.
3. Expression Trees: Though pointer-based is common, arrays can represent complete binary expression trees efficiently.
4. Game AI: Compact representation of decision trees in board games and simulations.
5. Competitive Programming: Array-based trees are often preferred for their speed and simplicity when dealing with complete structures.

Conclusion

Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.

GET FREE CHALLENGE