Start Learning Free
Previous Tutorial
22
DecBubble Sort in Data Structures
06 Jun 2024
Intermediate
8.55K Views
24 min read
Learn with an interactive course and practical hands-on labs
Free DSA Course with Certificate
Algorithm for Bubble Sort: An Overview
Bubble Sort is the easiest and the fundamental sorting algorithm in data structures. It works by repeatedly swapping the adjacent elements if they are in the wrong order. In this DSA tutorial, we will understand the Bubble Sort algorithm, implementation, complexity, etc.
To further enhance your understanding and application of bubble sort, consider enrolling in the best Data Structures and Algorithms Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.
What is Bubble Sort in Data Structures?
In this sorting method, the algorithm repeatedly compares the adjacent elements, from left to right, and swaps them if they are out-of-order. We start by comparing the first two elements of an array and swapping them if necessary so that the smaller one comes before the larger one. We then move on to compare the next two elements and perform the same swap if needed. This process continues until the array ends.
| More On Sorting Algo: 1. Selection Sort in Data Structures 2. Insertion Sort in Data Structures 3. Merge Sort in Data Structures 4. Quick Sort in Data Structures 5. Counting Sort in Data Structures |
Bubble Sort Algorithm
bubbleSort(array)
for i <- 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap leftElement and rightElement
end bubbleSort
Working of Bubble Sort Algorithm
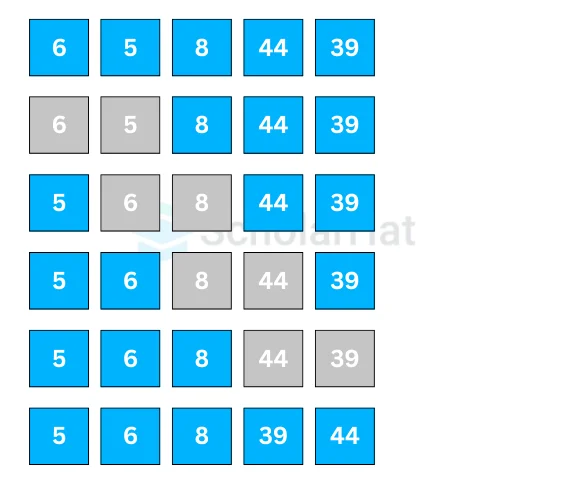
Let's suppose we have to sort the elements in ascending order.- First Iteration (Compare and Swap)
- Starting from the first index, compare the first and the second elements.
- If the first element is greater than the second element, they are swapped.
- Now, compare the second and the third elements. Swap them if they are not in order.
- The above process goes on until the last element.
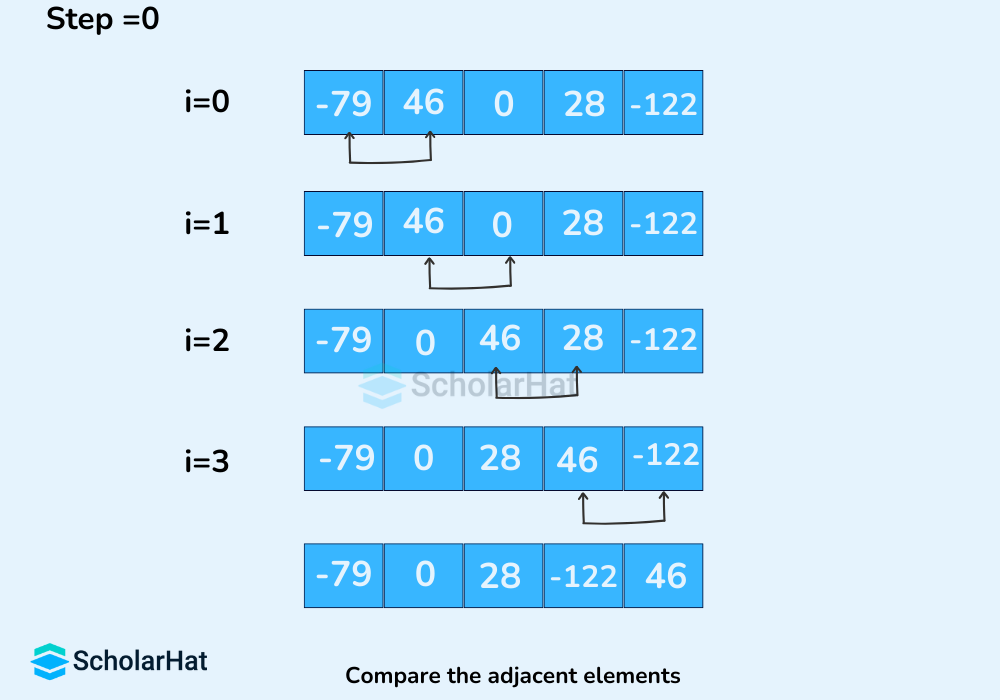
- Remaining Iteration
The same process goes on for the remaining iterations. After each iteration, the largest element among the unsorted elements is placed at the end.
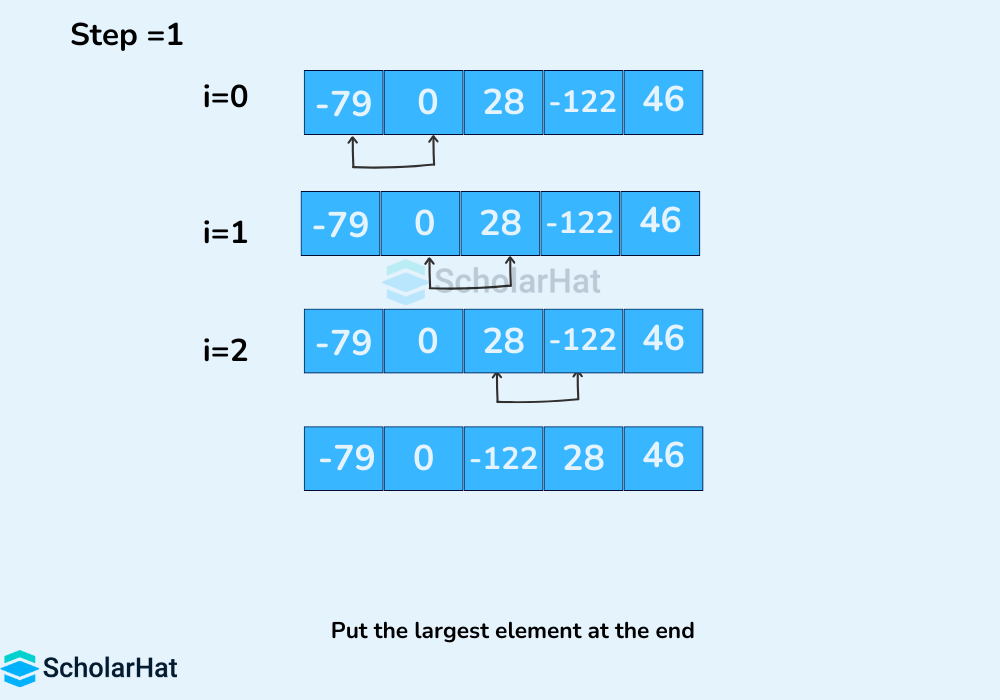
In each iteration, the comparison takes place up to the last unsorted element.
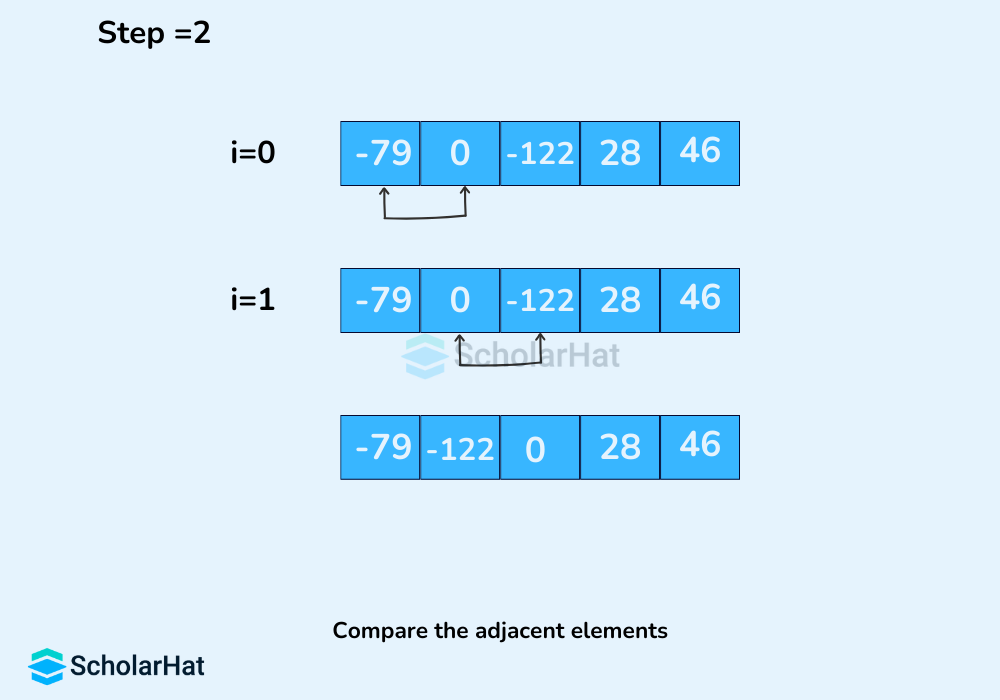
The array is sorted when all the unsorted elements are placed at their correct positions.
Read More - Data Structure Interview Questions for Experienced
Implementation of Bubble Sort in Different Languages in Data Structures(Python, Java & C++)
# Bubble sort in Python
def bubbleSort(array):
# Loop to access each array element
for i in range(len(array)):
# Loop to compare array elements
for j in range(0, len(array) - i - 1):
# Compare two adjacent elements
# Change > to < to sort in descending order
if array[j] > array[j + 1]:
# Swapping elements if they are not in the intended order
temp = array[j]
array[j] = array[j + 1]
array[j + 1] = temp
def print_list(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
arr = [-79, 46, 0, 28, -122]
# Print the original array
print('Original Array:', end=" ")
print_list(arr)
bubbleSort(arr)
# Print the sorted array in ascending order
print('Sorted Array in Ascending Order:', end=" ")
print_list(arr)
import java.util.Arrays;
public class BubbleSort {
public static void bubbleSort(int[] array) {
int n = array.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j + 1]) {
// Swapping elements if they are not in the intended order
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {-79, 46, 0, 28, -122};
// Print the original array
System.out.print("Original Array: ");
printArray(arr);
// Perform Bubble Sort
bubbleSort(arr);
// Print the sorted array in ascending order
System.out.print("Sorted Array in Ascending Order: ");
printArray(arr);
}
}
#include <iostream>
using namespace std;
void bubbleSort(int array[], int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size - i - 1; j++) {
if (array[j] > array[j + 1]) {
// Swapping elements if they are not in the intended order
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
int arr[] = {-79, 46, 0, 28, -122};
int size = sizeof(arr) / sizeof(arr[0]);
// Print the original array
cout << "Original Array: ";
printArray(arr, size);
// Perform Bubble Sort
bubbleSort(arr, size);
// Print the sorted array in ascending order
cout << "Sorted Array in Ascending Order: ";
printArray(arr, size);
return 0;
}
Output
Original Array: -122 46 0 28 -79
Sorted Array in Ascending Order: -122 -79 0 28 46
How to Optimize Bubble Sort in Data Structures?
In the above algorithm, all the comparisons are made even if the array is already sorted. This increases the execution time. To overcome this problem, we will introduce an extra variable "swapped". The value of "swapped" is set to true if there occurs a swapping of elements. Otherwise, it is set to false. After an iteration, if there is no swapping, the value of "swapped" will be false. This means elements are already sorted and there is no need to perform further iterations.
Optimized Bubble Sort Algorithm
bubbleSort(array)
swapped <- false
for i <- 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap leftElement and rightElement
swapped <- true
end bubbleSort
Implementation of Optimized Bubble Sort in Different Languages in Data Structures
def bubbleSort(array):
# loop through each element of array
for i in range(len(array)):
# keep track of swapping
swapped = False
# loop to compare array elements
for j in range(0, len(array) - i - 1):
# compare two adjacent elements
# change > to < to sort in descending order
if array[j] > array[j + 1]:
# swapping occurs if elements
# are not in the intended order
temp = array[j]
array[j] = array[j+1]
array[j+1] = temp
swapped = True
# no swapping means the array is already sorted
# so no need for further comparison
if not swapped:
break
def print_list(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
arr = [-79, 46, 0, 28, -122]
# Print the original array
print('Original Array:', end=" ")
print_list(arr)
bubbleSort(arr)
# Print the sorted array in ascending order
print('Sorted Array in Ascending Order:', end=" ")
print_list(arr)
import java.util.Arrays;
public class OptimizedBubbleSort {
public static void bubbleSort(int[] array) {
int n = array.length;
for (int i = 0; i < n; i++) {
boolean swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j + 1]) {
// Swapping elements if they are not in the intended order
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
swapped = true;
}
}
// No swapping means the array is already sorted
// So no need for further comparison
if (!swapped) {
break;
}
}
}
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {-79, 46, 0, 28, -122};
// Print the original array
System.out.print("Original Array: ");
printArray(arr);
// Perform Optimized Bubble Sort
bubbleSort(arr);
// Print the sorted array in ascending order
System.out.print("Sorted Array in Ascending Order: ");
printArray(arr);
}
}
#include <iostream>
using namespace std;
void bubbleSort(int array[], int size) {
for (int i = 0; i < size; i++) {
bool swapped = false;
for (int j = 0; j < size - i - 1; j++) {
if (array[j] > array[j + 1]) {
// Swapping elements if they are not in the intended order
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
swapped = true;
}
}
// No swapping means the array is already sorted
// So no need for further comparison
if (!swapped) {
break;
}
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
int arr[] = {-79, 46, 0, 28, -122};
int size = sizeof(arr) / sizeof(arr[0]);
// Print the original array
cout << "Original Array: ";
printArray(arr, size);
// Perform Optimized Bubble Sort
bubbleSort(arr, size);
// Print the sorted array in ascending order
cout << "Sorted Array in Ascending Order: ";
printArray(arr, size);
return 0;
}
Output
Original Array: -79 46 0 28 -122
Sorted Array in Ascending Order: -122 -79 0 28 46
Complexity Analysis of Bubble Sort Algorithm
- Time Complexity
Case Time Complexity Best O(n) Average O(n^2) Worst O(n^2) - Space Complexity: The space complexity of the simple bubble sort algorithm is O(1) due to the fixed number of variables, and we do not need any extra memory space apart from the loop variables and auxiliary variable that includes temp.
The space complexity of the optimized bubble sort algorithm is O(2). This is because we are using 2 extra variables – temp for swapping, and a flag variable called swapped.
Advantages of Bubble Sort
- Bubble sort is easy to understand and implement.
- It does not require any additional memory space.
- It is a stable sorting algorithm, meaning that elements with the same key value maintain their relative order in the sorted output.
Disadvantages of Bubble Sort
- Bubble sort has a time complexity of O(n^2) which makes it very slow for large data sets.
- Bubble sort is a comparison-based sorting algorithm, which means that it requires a comparison operator to determine the relative order of elements in the input data set. It can limit the efficiency of the algorithm in certain cases.
Summary
The use of the bubble sort algorithm in combination with other algorithms is a great way to maximize productivity and efficiency. We saw every aspect of the bubble sort algorithm in data structures. As it's the most basic sorting algorithm, understanding it is highly important. To apply your knowledge of the selection sort algorithm, enroll in our Data Structures Certification.
Similar Sorting Algorithms
FAQs
A bubble sort will take n-1 comparisons to sort a list of n elements.
It is called Bubble Sort because with each iteration, the largest element “bubbles up” to the top of the list.
The worst-case time complexity of a bubble sort algorithm is O(n^2). This means that, in the worst-case scenario, the algorithm will take n^2 steps to sort a list of n elements.
The data should be given in ascending order.