Complexity Analysis of Data Structures and Algorithms

Complexity Analysis of Data Structures and Algorithms: An Overview

How to find the most effective solution to a given problem from multiple solutions? It is through complexity analysis. Complexity analysis is defined as a technique to measure how long an algorithm would take to complete given an input of size n; independent of the machine, language, and compiler. It is used for evaluating the variations of execution time on different algorithms. While complexity is usually in terms of time, it is also analyzed in terms of space i.e. algorithm's memory requirements.

In this DSA tutorial, we will look in detail at every aspect of complexity analysis ranging from its need to the different types of complexities. If you want to enhance your practical understanding enroll in our Dsa Course.

Why Complexity Analysis is Required?

• It gives you an estimated time and space required to execute a program.
• It is used for comparing different algorithms for different input sizes.
• It helps to determine the difficulty of a problem.

Asymptotic Notations for Determining Complexities

Your algorithm doesn't need to behave in the same way for different input sizes. Its performance may vary. The study of the variations in the performance of the algorithm with the change in the order of the input size is called Asymptotic Analysis.

Asymptotic notations are mathematical notations to describe the running time of an algorithm when the input tends towards a particular value or a limiting value. In other words, it defines the mathematical limits of its run-time performance. Using the asymptotic analysis, we can easily conclude the average-case, best-case, and worst-case scenario of an algorithm.

There are mainly three asymptotic notations for the complexity analysis of algorithms. They are as follows:

1. Big-O notation
2. Omega notation
3. Theta notation

1. Big O notation (O-notation)

Big O notation symbolizes the upper bound of the running time of an algorithm or the algorithm's longest amount of time to complete its operation. Therefore, it gives the worst-case complexity of an algorithm.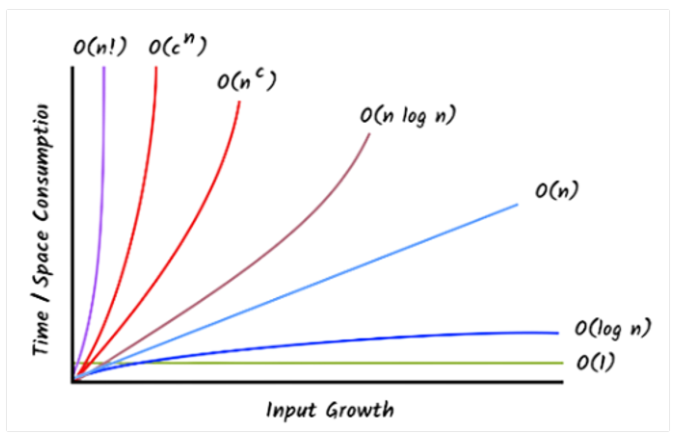

Mathematical Representation of Big-O Notation

O(g(n)) = { f(n): there exist positive constants c and n0
 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 } 

In the above expression, a function f(n) belongs to the set O(g(n)) if there exists a positive constant c such that it lies between 0 and cg(n), for sufficiently large n. For any value of n, the running time of an algorithm does not cross the time provided by O(g(n)).

We will look at the Big O notation in much detail in the next section, Big O Notation in Data Structures.

2. Omega notation (Ω-notation)

Omega notation symbolizes the lower bound of the running time of an algorithm. Thus, it provides the best-case complexity of an algorithm. It determines the fastest time that an algorithm can run.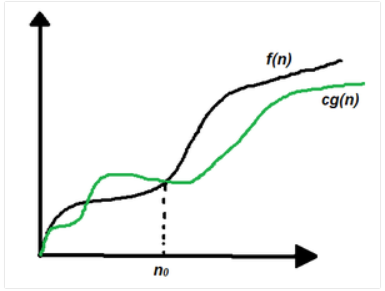

Mathematical Representation of Omega Notation

Ω(g(n)) = { f(n): there exist positive constants c and n0 
 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }

In the above expression, a function f(n) belongs to the set Ω(g(n)) if there exists a positive constant c such that it lies above cg(n), for sufficiently large n. For any value of n, the minimum time required by the algorithm is given by Omega Ω(g(n)).

3. Theta Notation (Θ-notation)

Theta notation symbolizes the upper and the lower bound of the running time of an algorithm. In real-world problems, an algorithm does not perform worst or best, it fluctuates between the worst-case and best-case, and this gives us the average case complexity of an algorithm.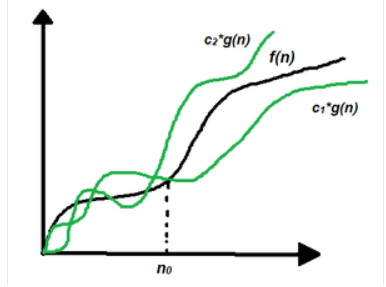

Mathematical Representation of Theta Notation

Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0
 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }

In the above expression, a function f(n) belongs to the set Θ(g(n)) if there exist positive constants c1 and c2 such that it can be sandwiched between c1g(n) and c2g(n), for sufficiently large n. If a function f(n) lies anywhere in between c1g(n) and c2g(n) for all n ≥ n0, then f(n) is said to be asymptotically tight bound.

Read More - DSA Interview Questions and Answers

Parameters to Measure Complexities

1. Time Complexity

Time complexity is the amount of time taken by an algorithm to execute each statement of the code till its completion. The time taken here is for the function of the length of the input and not the actual execution time of the machine on which the algorithm is running. The time complexity of algorithms is commonly expressed using the Big O notation.

To calculate the time complexity, total the cost of each fundamental instruction and the number of times the instruction is executed.

• There are statements with basic operations like comparisons, return statements, assignments, and reading a variable. Let's assume that each statement takes constant time O(1).

  Example

  int a=5; // reading a variable
  if( a==5) return true; // return statement
  int x= 4>5 ? 1:0; // comparison
  bool flag=true; // Assignment

  Total time taken, T(n) = t(statement1) + t(statement2) + ... + t(statementN); 
  T(n)=O(1) i.e. constant complexity
  

  Here, n is the input size, and t represents the amount of time that a statement or collection of statements takes to execute.
• To calculate the time taken by any loop, find out the runtime of the loop block and multiply it by the number of times the program will repeat the loop.

  Example

  for (int i = 0; i < n; i++) {
   cout << “ScholarHat” << endl;
  }
  

  In the above code, the loop will execute n times, and it will print ScholarHat N times.

  Total time taken, T(N) = n *( t(cout statement))
   = n * O(1)
   = O(n) i.e. Linear complexity.
  

2. Space Complexity

Space complexity is the amount of memory space an algorithm or a problem takes during the execution of that particular problem/algorithm. Here, the space used includes both, the variables and the input values. Space complexity is the combination or sum up of the auxiliary space and the space used by input values. Auxiliary space is the temporary space required by an algorithm/problem during the execution of that algorithm/problem.

Space Complexity = Auxiliary Space + Space used for input values. It is frequently represented using Big O notation, just like time complexity, to describe the maximum amount of memory utilization. To get the space complexity, one must know the amount of memory used by different types of datatype variables, program instructions, constant values, and things like function calls, recursion stacks, etc.

Let's calculate the space complexity for the code of Addition of Numbers

Example

{ 
 int sum = x + y;
 return sum;
}

In the above code, we have 3 integer variables sum, x, and y. All the variables will take 4 bytes of space, and an extra 4-byte for the return value sum. Hence, the total space complexity = 4*4 + 4 = 20 bytes. This is the fixed complexity and because of the same type of inputs, such space complexities are considered as constant space complexities or so-called O(1) space complexity.

How to optimize an Algorithm?

We can optimize a solution using both time and space optimization. To optimize a program,

• Reduce the time taken to run the program and increase the space occupied.
• Reduce the memory usage of the program and increase its total run time.
• Reduce both time and space complexity by deploying relevant algorithms.

Common Asymptotic Notations

Type of Complexity	Asymptotic Notation
constant	?(1)
linear	?(n)
logarithmic	?(log n)
n log n	?(n log n)
exponential	2?(n)
cubic	?(n3)
polynomial	n?(1)
quadratic	?(n2)

Complexity Analysis Of Algorithms

Algorithm	Complexity
Linear Search Algorithm	O(N)
Binary Search	O(LogN)
Bubble Sort	O(N^2)
Insertion Sort	O(N^2)
Selection Sort	O(N^2)
QuickSort	O(N^2)
Merge Sort	O(N log(N))
Radix Sort	O((n+b) * logb(k)).
Breadth First Search	O(V+E)
Depth First Search	O(V+E)

Worst-case time complexity of different data structures for different operations

Data structure	Access	Search	Insertion	Deletion
Array	O(1)	O(N)	O(N)	O(N)
Stack	O(N)	O(N)	O(1)	O(1)
Queue	O(N)	O(N)	O(1)	O(1)
Singly Linked List	O(N)	O(N)	O(N)	O(N)
Doubly Linked List	O(N)	O(N)	O(1)	O(1)
Hash Table	O(N)	O(N)	O(N)	O(N)
Binary Search Tree	O(N)	O(N)	O(N)	O(N)
AVL Tree	O(log N)	O(log N)	O(log N)	O(log N)
Binary Tree	O(N)	O(N)	O(N)	O(N)
Red Black Tree	O(log N)	O(log N)	O(log N)	O(log N)

Summary

While going through this tutorial, I know you will feel difficulties in understanding as the concepts are quite new and a little advanced. But don't worry, if you refer to this again and again, you will grasp it thoroughly. The programmer uses the outcome of the algorithmic analysis as a guideline for program development, and the complexities prevent him from the incorrect choices in designing a solution to the program. For the implementation of your theoretical knowledge consider our, Data Structures and Algorithms Certification course.