Divide and Conquer Algorithm in Data Structures - Its Working, Advantages & Disadvantages

Divide and Conquer Algorithm: An Overview

Divide and Conquer Algorithm is a problem-solving method in Data Structures working on recursion principle. We had seen this in brief in the Data Structures and Algorithms tutorial. In this DSA tutorial, we will discuss the Divide and Conquer Algorithm with its working, implementation, etc. To further enhance your understanding and application of Divide and Conquer, consider enrolling in the best Data Structures and Algorithms Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Divide and Conquer Algorithm in Data Structures?

According to the name, the divide and Conquer Algorithm involves breaking down a complex task into smaller, more manageable sub-problems, solving them independently, and then merging the results to obtain the final solution. In this, we keep dividing the given problem into smaller problems to the point that these smaller sub-problems can no longer be further divided.

Working of Divide and Conquer Algorithm

The following three steps are involved in the working of Divide and Conquer Algorithm:

1. Divide: Divide the given problem into sub-problems until none of the sub-problems are further divisible using recursion.
2. Conquer: Solve the smaller sub-problems recursively. If the subproblem is small enough, then solve it directly.
3. Combine: Recursively combine the individual solutions of the sub-problems obtained from the previous stage of the algorithm that are part of the recursive process to solve the actual problem.

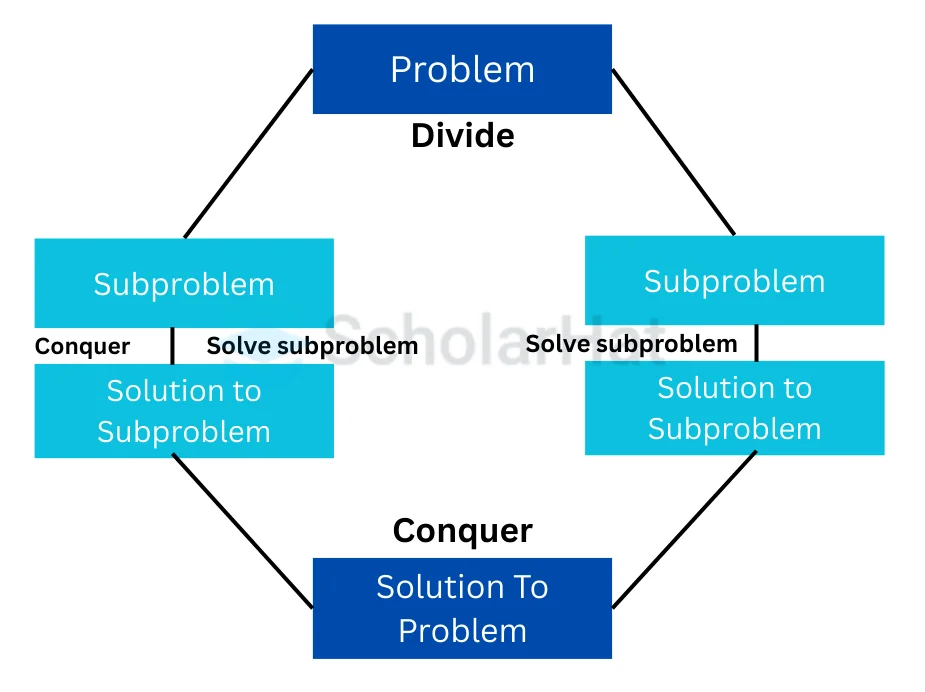
One can observe that recursion is at the core of the divide-and-conquer algorithms. Whether it is breaking down the original problem into sub-problems or merging the individual solutions into the final solutions, both tasks are done recursively. Thus, to establish a strong understanding of the divide and conquer approach, a good understanding of recursion is mandatory.

Learn more:

• Recursion in C++
• Recursion in C

Example of Divide and Conquer Algorithm

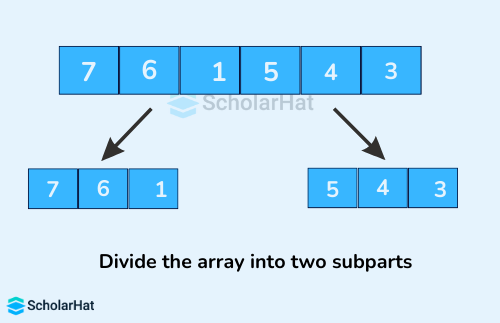
Here, we will sort an array using the divide and conquer approach (ie. merge sort).

1. Let the given array be

   

2. Divide the array into two halves.

   

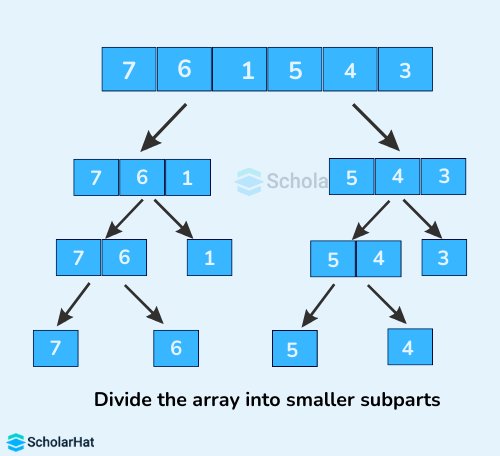
   Again, divide each subpart recursively into two halves until you get individual elements.

   

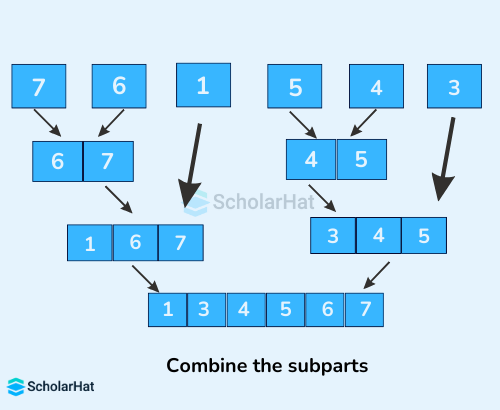
3. Now, combine the individual elements in a sorted manner. Here, conquer and combine steps go side by side.

   

Read More - Data Structure Interview Questions for Freshers

Time Complexity of Divide and Conquer Algorithm

The complexity of the divide and conquer algorithm is calculated using the master theorem.

T(n) = aT(n/b) + f(n),
where,
n = size of input
a = number of subproblems in the recursion
n/b = size of each subproblem. All subproblems are assumed to have the same size.
f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions   

Divide and Conquer vs the Dynamic Programming Approach

Both the divide and conquer and the dynamic programming algorithms share a common characteristic: the initial problem is divided into smaller sub-problems, and then the final solution is generated in a bottom-up approach where the resultant outputs of the subproblems are combined into the final solution.

The difference lies in how the sub-problems are solved and merged into the final solution.

1. The divide and conquer approach divides a problem into smaller subproblems; these subproblems are further solved recursively. The result of each subproblem is not stored for future reference, whereas, in a dynamic approach, the result of each subproblem is stored for future reference.
2. Use the divide and conquer approach when the same subproblem is not solved multiple times. Use the dynamic approach when the result of a subproblem is to be used multiple times in the future.

Let's take an example to find the Fibonacci series.

Divide and Conquer Approach

fib(n)
    If n < 2, return 1
    Else , return f(n - 1) + f(n -2)  

Dynamic Approach

mem = []
fib(n)
    If n in mem: return mem[n] 
    else,     
        If n < 2, f = 1
        else , f = f(n - 1) + f(n -2)
        mem[n] = f
        return f

Here, we are storing the result of each sub-problem in the memory array, mem. These stored solutions can then be referenced and reused in the future as we are further solving the problem.

Advantages of Divide and Conquer Algorithms

1. Efficiency: Divide and Conquer algorithms often provide efficient solutions to problems. By breaking down a problem into smaller parts, the algorithm can reduce the overall time complexity of the solution.
2. Parallelization: They are used in multi-processor machines having shared-memory systems where the communication of data between processors does not need to be planned because distinct sub-problems can be executed on different processors.
3. Modularity: The algorithm promotes modularity by dividing a complex problem into manageable subproblems. Each subproblem can be solved separately and then combined with other subproblem solutions to obtain the final result.
4. Algorithmic reusability: The Divide and Conquer approach is often based on recurring patterns. Once a general divide-and-conquer algorithm is designed, it can be applied to problems with similar characteristics.
5. Solving large instances: Divide and Conquer algorithms are particularly useful when dealing with large problem instances. By dividing the problem into smaller subproblems, the algorithm can handle larger inputs more efficiently.
6. Optimality: In many cases, these algorithms produce optimal solutions. By solving subproblems optimally and combining the results correctly, the algorithm can guarantee an optimal solution for the overall problem.

Disadvantages of Divide and Conquer Algorithm

• Extra Memory Usage: In some cases, the divide and conquer approach requires additional memory to store intermediate results during the recursive process. This can be a disadvantage, especially when dealing with large input sizes or limited memory resources.
• Difficulty Handling Some Problems: Not all problems can be easily solved using the divide and conquer paradigm. Some problems may not have a natural division, or the division process may introduce additional complexities that make the algorithm less efficient or harder to implement correctly.
• Suboptimal Solutions: The divide and conquer strategy sometimes guarantees the most optimal solution. Although it often leads to efficient solutions, there are cases where alternative algorithms can outperform divide-and-conquer approaches in terms of time or space complexity.
• Not Always Stable: Divide and conquer algorithms may not preserve the order of elements in the input.
• Potential for Overlapping Subproblems: Some divide-and-conquer algorithms may encounter overlapping subproblems, meaning that the same subproblem is solved multiple times. Without proper techniques to handle overlapping subproblems, the algorithm can become inefficient due to redundant computations

Summary

Hence, Divide and Conquer algorithm is a powerful tool for solving complex problems with ease. It reduces the complexity of its operations into a series of smaller problems that can be more easily solved, allowing for faster problem-solving processes. This has seen it being used extensively in computer science, mathematics, engineering, cryptography, and many other fields. To test your knowledge of the Divide and Conquer algorithm, enroll in our Dsa Training.