Which approach Greedy Algorithm follows

divIt works in a topdown approachdiv

What are the two properties of Greedy Algorithms

olliGreedy Choice PropertynbspliliOptimal Substructureliol

Greedy Algorithm in Data Structures

Q: Are Greedy Algorithms faster than Dynamic Programming

divYes Greedy algorithms are very fast compared to their alternatives such as dynamic programmingdiv

23 Jul 2025

Intermediate

11.6K Views

114 min read

Data Structures Greedy Algorithm

A greedy algorithm is a problem-solving technique used in data structures and algorithms where the solution is built step-by-step by making the most optimal choice at each step. The idea is to choose the option that seems best at the moment—a locally optimal choice—with the hope that these choices will lead to a globally optimal solution.

Think of a greedy algorithm like planning a road trip. At every intersection, you pick the shortest-looking path to reach your destination quickly. It seems smart at the moment, right? But sometimes that path leads to traffic or a dead end.

That’s how a greedy algorithm works—it makes the best immediate choice, without thinking ahead. It’s fast and simple but doesn’t always guarantee the best overall solution.In this DSA tutorial, we will see how the Greedy Algorithm in Data Structures works.

To deepen your understanding of Greedy Algorithms and other essential concepts in DSA, consider joining a Data Structures and Algorithms Course. This course provides hands-on experience, real-world examples, and expert guidance to help you master DSA and achieve success in technical interviews.

What is a Greedy Algorithm in Data Structures?

A Greedy Algorithm is a popular problem-solving technique used in data structures that makes decisions based on the best immediate (local) choice at each step. It does not revisit or revise earlier decisions, even if a better path becomes clear later.

Key Features:

Step-by-step optimization by choosing the best available option at each point.
No backtracking or re-evaluation of previous choices.
Follows a top-down approach.
Fast and intuitive, making it ideal for scenarios with limited time or resources.

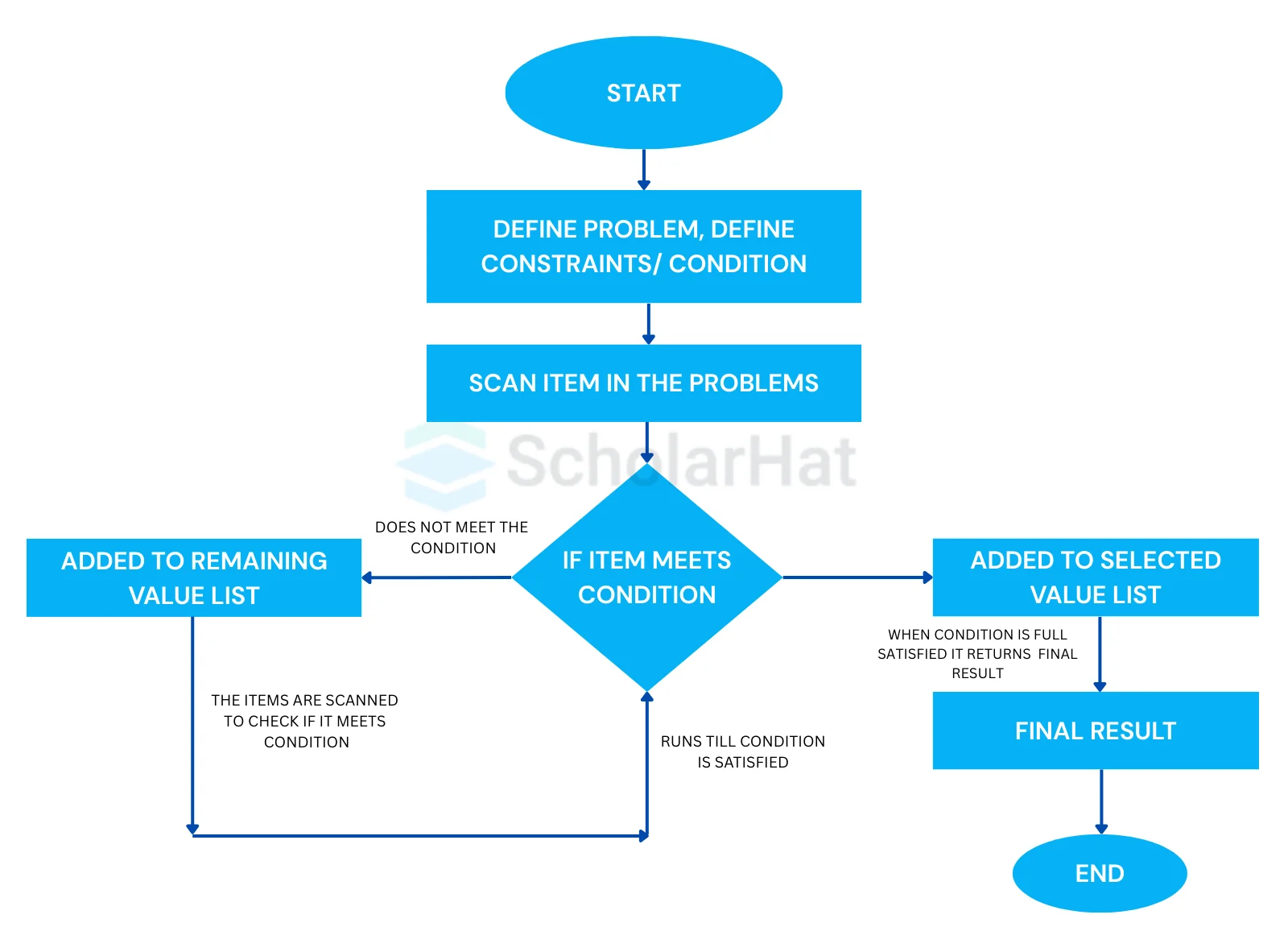
We can determine if the algorithm can be used with any optimization problem if the problem satisfies the following two properties:

Greedy Choice Property

If an optimal solution to the problem can be found by choosing the best choice at each step without reconsidering the previous steps once chosen, the problem can be solved using a greedy approach.

Optimal Substructure

If the optimal overall solution to the problem corresponds to the optimal solution to its subproblems, then the problem can be solved using a greedy approach.

Greedy Algorithm Characteristics

1. Makes Locally Optimal Choices- Greedy algorithms make decisions based on the current best option, aiming to optimize the solution step-by-step. It does not look ahead or revisit previous steps, making it efficient but sometimes shortsighted.

2. Irrevocable Decisions- Once a choice is made, it cannot be changed later. This makes greedy algorithms fast but sometimes unable to correct earlier mistakes, especially in complex scenarios.

3. May Not Always Produce the Best Global Solution- While greedy algorithms work well for many problems, they do not always guarantee a globally optimal result. In some cases, like the Travelling Salesman Problem, they can even produce the worst-case output.

4. Faster Than Alternatives Like Dynamic Programming- Greedy algorithms are generally faster and use less memory compared to approaches like dynamic programming, which considers all possible combinations and requires storing intermediate results.

5. Intuitive but Hard to Prove Mathematically- Greedy algorithms are easy to understand and implement, but mathematically proving their correctness can be complex. Not all problems are suitable for greedy strategies.

6. Suitable for Approximation in Complex Problems- In problems where finding an exact solution is computationally infeasible, greedy algorithms can provide a near-optimal or approximate solution that is good enough for practical use.

Architecture Of The Greedy Algorithm

Input to Algorithm: Function = F, Set of Inputs = C

Output: Solution Set which maximizes or minimizes function

1. Initialize an empty solution set, S = {}
2. While (C is not empty):
    # step 1: choose an item from C
    current_choice = Select(C)
    
    # step 2: if current_choice is feasable, add to S
    if(isFeasable(current_choice)):
        S.add(C)
    
    # step 3: remove the current_choice from C
    C.remove(current_choice)
3. Return S

Here, the Select() function makes a greedy choice from the input set C. isFeasable() function checks whether the choice made by the Select() function leads to an optimal value of F

As per the algorithm,

Initially, the solution set (containing answers) is empty.
At each step, an item is added to the solution set until a solution is reached.
If the solution set is feasible, the current item is kept.
Otherwise, the item is rejected and never considered again.

Example of Problem-Solving Using a Greedy Algorithm

Problem: You have to make a change of an amount using the smallest possible number of coins.
Amount: $22

Available coins are
  $5 coin
  $2 coin
  $2 coin
There is no limit to the number of each coin you can use.

Solution:

Create an empty solution-set = { }. Available coins are {5, 2, 2}.
We are supposed to find the sum = 20. Let's start with sum = 0.
Always select the coin with the largest value (i.e. 5) until the sum > 20. (When we select the largest value at each step, we hope to reach the destination faster. This concept is called greedy choice property.)
In the first iteration, solution-set = {5} and sum = 5.
In the second iteration, solution-set = {5, 5} and sum = 10.
In the third iteration, solution-set = {5, 5, 5} and sum = 15.
In the fourth iteration, solution-set = {5, 5, 5, 5} and sum = 20. (We cannot select 5 here because if we do so, sum = 20 which is greater than 18. So, we select the 2nd largest item which is 2).
In the fifth iteration, select 2. Now sum = 22 and solution-set = {5, 5, 5, 5, 2}. (We cannot select 5 here because if we do so, sum = 25 which is greater than 20. So, we select the 2nd largest item which is 2).

Types of Greedy Algorithms in Data Structure

Greedy algorithm

Greedy Algorithm Problems

This table summarizes Easy, Medium, and Hard problems on the Greedy Algorithm with their inputs and outputs.

Difficulty Level	Problem	Description
Easy	Activity Selection Problem	Select the maximum number of non-overlapping activities.
Easy	Fractional Knapsack Problem	Maximize the total value of items in a knapsack with fractional parts allowed.
Easy	Minimum Coins Problem	Find the minimum number of coins required for a given amount.
Easy	Huffman Encoding	Generate a binary prefix code for characters based on frequency.
Easy	N Meetings in One Room	Schedule the maximum number of meetings in one room.
Medium	Job Sequencing Problem	Schedule jobs to maximize profit within deadlines.
Medium	Candy Distribution Problem	Distribute candies such that higher-rated children get more.
Medium	Connecting Ropes to Minimize Cost	Connect ropes with minimum cost.
Medium	Maximum Length Chain of Pairs	Find the longest chain of pairs (a, b) followed by (c, d).
Medium	Gas Station Problem	Complete a circular tour visiting gas stations.
Hard	Minimum Platforms	Find the minimum platforms needed for trains to avoid collision.
Hard	Maximum Subarray XOR	Find the subset of an array that gives the maximum XOR value.
Hard	Prim’s Minimum Spanning Tree	Find the minimum spanning tree for a weighted graph.
Hard	Dijkstra’s Shortest Path Algorithm	Find the shortest path from a source vertex to all other vertices.
Hard	Optimal File Merge Pattern	Merge files with the minimum computation cost.

Easy Problems on Greedy Algorithm

1. Activity Selection Problem

Problem: Given n activities with start and finish times, select the maximum number of activities that don’t overlap.

Approach:

Sort activities by their finish time.
Select the activity that finishes first and ensure it doesn’t overlap with the previously selected one.

Code:


#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<pair<int, int>> activitySelection(vector<int>& start, vector<int>& end) {
    vector<pair<int, int>> activities, selected;
    int n = start.size();

    for (int i = 0; i < n; i++) {
        activities.push_back({start[i], end[i]});
    }
    sort(activities.begin(), activities.end(), [](auto& a, auto& b) {
        return a.second < b.second;
    });

    int last_end_time = 0;
    for (auto& activity : activities) {
        if (activity.first >= last_end_time) {
            selected.push_back(activity);
            last_end_time = activity.second;
        }
    }
    return selected;
}

int main() {
    vector<int> start = {1, 3, 0, 5, 8, 5};
    vector<int> end = {2, 4, 6, 7, 9, 9};

    vector<pair<int, int>> result = activitySelection(start, end);

    cout << "Selected Activities: ";
    for (auto& activity : result) {
        cout << "(" << activity.first << ", " << activity.second << ") ";
    }
    cout << endl;

    return 0;
}


using System;
using System.Collections.Generic;

class Program {
    static List<(int, int)> ActivitySelection(int[] start, int[] end) {
        var activities = new List<(int, int)>();
        for (int i = 0; i < start.Length; i++) {
            activities.Add((start[i], end[i]));
        }
        activities.Sort((a, b) => a.Item2.CompareTo(b.Item2));

        var selected = new List<(int, int)>();
        int lastEndTime = 0;

        foreach (var (s, e) in activities) {
            if (s >= lastEndTime) {
                selected.Add((s, e));
                lastEndTime = e;
            }
        }

        return selected;
    }

    static void Main() {
        int[] start = { 1, 3, 0, 5, 8, 5 };
        int[] end = { 2, 4, 6, 7, 9, 9 };

        var result = ActivitySelection(start, end);

        Console.WriteLine("Selected Activities:");
        foreach (var (s, e) in result) {
            Console.WriteLine($"({s}, {e})");
        }
    }
}


def activity_selection(start, end):
    activities = list(zip(start, end))
    activities.sort(key=lambda x: x[1])  # Sort by end time

    selected = []
    last_end_time = 0

    for s, e in activities:
        if s >= last_end_time:
            selected.append((s, e))
            last_end_time = e

    return selected

# Example usage
start = [1, 3, 0, 5, 8, 5]
end = [2, 4, 6, 7, 9, 9]
result = activity_selection(start, end)
print("Selected Activities:", result)


import java.util.*;

public class ActivitySelection {
    public static List<int[]> activitySelection(int[] start, int[] end) {
        List<int[]> activities = new ArrayList<>();
        for (int i = 0; i < start.length; i++) {
            activities.add(new int[]{start[i], end[i]});
        }
        activities.sort(Comparator.comparingInt(a -> a[1]));

        List<int[]> selected = new ArrayList<>();
        int lastEndTime = 0;

        for (int[] activity : activities) {
            if (activity[0] >= lastEndTime) {
                selected.add(activity);
                lastEndTime = activity[1];
            }
        }

        return selected;
    }

    public static void main(String[] args) {
        int[] start = {1, 3, 0, 5, 8, 5};
        int[] end = {2, 4, 6, 7, 9, 9};

        List<int[]> result = activitySelection(start, end);

        System.out.println("Selected Activities:");
        for (int[] activity : result) {
            System.out.println("(" + activity[0] + ", " + activity[1] + ")");
        }
    }
}


function activitySelection(start: number[], end: number[]): [number, number][] {
    const activities = start.map((s, i) => [s, end[i]] as [number, number]);
    activities.sort((a, b) => a[1] - b[1]);

    const selected: [number, number][] = [];
    let lastEndTime = 0;

    for (const [s, e] of activities) {
        if (s >= lastEndTime) {
            selected.push([s, e]);
            lastEndTime = e;
        }
    }

    return selected;
}

// Example usage
const start = [1, 3, 0, 5, 8, 5];
const end = [2, 4, 6, 7, 9, 9];
const result = activitySelection(start, end);
console.log("Selected Activities:", result);

Explanation: The code sorts the activities by their ending time, ensuring we pick the ones that leave the most room for subsequent activities.

2. Fractional Knapsack Problem

Problem: Maximize value by putting items in a knapsack where fractional parts of an item are allowed.

Approach:

Calculate the value/weight for each item.
Sort items by this ratio in descending order.
Pick as much as possible from the highest value/weight item.

Code:


#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Item {
    double value, weight;
};

// Comparator function to sort items by value/weight ratio
bool cmp(Item a, Item b) {
    return (a.value / a.weight) > (b.value / b.weight);
}

double fractionalKnapsack(vector<Item> items, double capacity) {
    sort(items.begin(), items.end(), cmp);

    double totalValue = 0.0;

    for (auto item : items) {
        if (capacity >= item.weight) {
            totalValue += item.value;
            capacity -= item.weight;
        } else {
            totalValue += item.value * (capacity / item.weight);
            break;
        }
    }
    return totalValue;
}

int main() {
    vector<Item> items = {{60, 10}, {100, 20}, {120, 30}};
    double capacity = 50;
    cout << "Maximum value: " << fractionalKnapsack(items, capacity) << endl;
    return 0;
}


using System;
using System.Collections.Generic;

class Item {
    public double Value { get; set; }
    public double Weight { get; set; }
}

class FractionalKnapsack {
    public static double MaximizeValue(List<Item> items, double capacity) {
        items.Sort((a, b) => (b.Value / b.Weight).CompareTo(a.Value / a.Weight));

        double totalValue = 0.0;

        foreach (var item in items) {
            if (capacity >= item.Weight) {
                totalValue += item.Value;
                capacity -= item.Weight;
            } else {
                totalValue += item.Value * (capacity / item.Weight);
                break;
            }
        }
        return totalValue;
    }

    static void Main(string[] args) {
        List<Item> items = new List<Item> {
            new Item { Value = 60, Weight = 10 },
            new Item { Value = 100, Weight = 20 },
            new Item { Value = 120, Weight = 30 }
        };
        double capacity = 50;
        Console.WriteLine("Maximum value: " + MaximizeValue(items, capacity));
    }
}


def fractional_knapsack(values, weights, capacity):
    items = list(zip(values, weights))
    items.sort(key=lambda x: x[0] / x[1], reverse=True)  # Sort by value/weight ratio

    total_value = 0
    for value, weight in items:
        if capacity >= weight:
            total_value += value
            capacity -= weight
        else:
            total_value += value * (capacity / weight)
            break

    return total_value

# Example usage
values = [60, 100, 120]
weights = [10, 20, 30]
capacity = 50
result = fractional_knapsack(values, weights, capacity)
print("Maximum value:", result)


import java.util.*;

class Item {
    double value, weight;

    Item(double value, double weight) {
        this.value = value;
        this.weight = weight;
    }
}

public class FractionalKnapsack {
    public static double maximizeValue(List<Item> items, double capacity) {
        items.sort((a, b) -> Double.compare(b.value / b.weight, a.value / a.weight));

        double totalValue = 0.0;

        for (Item item : items) {
            if (capacity >= item.weight) {
                totalValue += item.value;
                capacity -= item.weight;
            } else {
                totalValue += item.value * (capacity / item.weight);
                break;
            }
        }
        return totalValue;
    }

    public static void main(String[] args) {
        List<Item> items = Arrays.asList(new Item(60, 10), new Item(100, 20), new Item(120, 30));
        double capacity = 50;
        System.out.println("Maximum value: " + maximizeValue(items, capacity));
    }
}


class Item {
    constructor(public value: number, public weight: number) {}
}

function fractionalKnapsack(items: Item[], capacity: number): number {
    items.sort((a, b) => (b.value / b.weight) - (a.value / a.weight));

    let totalValue = 0;

    for (const item of items) {
        if (capacity >= item.weight) {
            totalValue += item.value;
            capacity -= item.weight;
        } else {
            totalValue += item.value * (capacity / item.weight);
            break;
        }
    }

    return totalValue;
}

// Example usage
const items = [new Item(60, 10), new Item(100, 20), new Item(120, 30)];
const capacity = 50;
console.log("Maximum value:", fractionalKnapsack(items, capacity));

Explanation: The algorithm prioritizes the items with the highest value-to-weight ratio and fills the knapsack fractionally when necessary.

3. Minimum Coins Problem

Problem: Given a set of denominations, find the minimum coins needed for a given amount.

Approach:

Sort denominations in descending order.
Use as many of the largest denominations as possible, then move to the next.

Code:


#include <iostream>
#include <vector>
#include <algorithm>

int minimumCoins(std::vector<int>& coins, int amount) {
    std::sort(coins.rbegin(), coins.rend());
    int count = 0;

    for (int coin : coins) {
        if (amount == 0) break;
        count += amount / coin;
        amount %= coin;
    }

    return count;
}

int main() {
    std::vector<int> coins = {1, 2, 5, 10, 20, 50, 100, 500};
    int amount = 93;

    int result = minimumCoins(coins, amount);
    std::cout << "Minimum coins required: " << result << std::endl;

    return 0;
}


using System;
using System.Linq;

class Program {
    static int MinimumCoins(int[] coins, int amount) {
        Array.Sort(coins, (a, b) => b.CompareTo(a));
        int count = 0;

        foreach (int coin in coins) {
            if (amount == 0) break;
            count += amount / coin;
            amount %= coin;
        }

        return count;
    }

    static void Main() {
        int[] coins = {1, 2, 5, 10, 20, 50, 100, 500};
        int amount = 93;

        int result = MinimumCoins(coins, amount);
        Console.WriteLine("Minimum coins required: " + result);
    }
}


def minimum_coins(coins, amount):
    coins.sort(reverse=True)
    count = 0
    for coin in coins:
        if amount == 0:
            break
        count += amount // coin
        amount %= coin

    return count

# Example usage
coins = [1, 2, 5, 10, 20, 50, 100, 500]
amount = 93
result = minimum_coins(coins, amount)
print("Minimum coins required:", result)


import java.util.Arrays;

public class MinimumCoins {
    public static int minimumCoins(int[] coins, int amount) {
        Arrays.sort(coins);
        int count = 0;

        for (int i = coins.length - 1; i >= 0; i--) {
            if (amount == 0) break;
            count += amount / coins[i];
            amount %= coins[i];
        }

        return count;
    }

    public static void main(String[] args) {
        int[] coins = {1, 2, 5, 10, 20, 50, 100, 500};
        int amount = 93;

        int result = minimumCoins(coins, amount);
        System.out.println("Minimum coins required: " + result);
    }
}


function minimumCoins(coins: number[], amount: number): number {
    coins.sort((a, b) => b - a);
    let count = 0;

    for (let coin of coins) {
        if (amount === 0) break;
        count += Math.floor(amount / coin);
        amount %= coin;
    }

    return count;
}

// Example usage
const coins: number[] = [1, 2, 5, 10, 20, 50, 100, 500];
const amount: number = 93;
const result: number = minimumCoins(coins, amount);
console.log("Minimum coins required:", result);

Explanation: This greedy approach ensures the use of the largest denominations first, minimizing the number of coins.

4. Huffman Encoding

Problem: Generate prefix codes for characters based on their frequencies.

Approach:

Use a priority queue to build a Huffman tree.
Assign binary codes based on tree traversal.

Code:


#include <iostream>
#include <vector>
#include <queue>
#include <map>
#include <string>
#include <algorithm>

using namespace std;

struct Node {
    char ch;
    int freq;
    Node *left, *right;
    Node(char c, int f) : ch(c), freq(f), left(nullptr), right(nullptr) {}
};

struct Compare {
    bool operator()(Node* l, Node* r) {
        return l->freq > r->freq;
    }
};

void generateCodes(Node* root, string code, map<char, string>& huffmanCodes) {
    if (!root) return;
    if (root->ch != '\0') huffmanCodes[root->ch] = code;
    generateCodes(root->left, code + "0", huffmanCodes);
    generateCodes(root->right, code + "1", huffmanCodes);
}

vector<pair<char, string>> huffmanEncoding(map<char, int>& freq) {
    priority_queue<Node*, vector<Node*>, Compare> minHeap;
    for (auto& p : freq) minHeap.push(new Node(p.first, p.second));

    while (minHeap.size() > 1) {
        Node* left = minHeap.top(); minHeap.pop();
        Node* right = minHeap.top(); minHeap.pop();
        Node* sum = new Node('\0', left->freq + right->freq);
        sum->left = left;
        sum->right = right;
        minHeap.push(sum);
    }

    Node* root = minHeap.top();
    map<char, string> huffmanCodes;
    generateCodes(root, "", huffmanCodes);

    vector<pair<char, string>> result(huffmanCodes.begin(), huffmanCodes.end());
    sort(result.begin(), result.end(), [](auto& a, auto& b) {
        return a.second.length() < b.second.length();
    });

    return result;
}

int main() {
    map<char, int> freq = {{'a', 5}, {'b', 9}, {'c', 12}, {'d', 13}, {'e', 16}, {'f', 45}};
    auto result = huffmanEncoding(freq);
    cout << "Huffman Codes:" << endl;
    for (auto& p : result) cout << p.first << ": " << p.second << endl;
    return 0;
}


using System;
using System.Collections.Generic;
using System.Linq;

class HuffmanNode : IComparable<HuffmanNode> {
    public char Char { get; set; }
    public int Frequency { get; set; }
    public HuffmanNode Left { get; set; }
    public HuffmanNode Right { get; set; }

    public int CompareTo(HuffmanNode other) {
        return Frequency - other.Frequency;
    }
}

class Program {
    static void GenerateCodes(HuffmanNode node, string code, Dictionary<char, string> huffmanCodes) {
        if (node == null) return;
        if (node.Char != '\0') huffmanCodes[node.Char] = code;
        GenerateCodes(node.Left, code + "0", huffmanCodes);
        GenerateCodes(node.Right, code + "1", huffmanCodes);
    }

    static List<KeyValuePair<char, string>> HuffmanEncoding(Dictionary<char, int> freq) {
        var priorityQueue = new SortedSet<HuffmanNode>();
        foreach (var kvp in freq) priorityQueue.Add(new HuffmanNode { Char = kvp.Key, Frequency = kvp.Value });

        while (priorityQueue.Count > 1) {
            var left = priorityQueue.Min; priorityQueue.Remove(left);
            var right = priorityQueue.Min; priorityQueue.Remove(right);

            var sumNode = new HuffmanNode {
                Char = '\0',
                Frequency = left.Frequency + right.Frequency,
                Left = left,
                Right = right
            };

            priorityQueue.Add(sumNode);
        }

        var root = priorityQueue.Min;
        var huffmanCodes = new Dictionary<char, string>();
        GenerateCodes(root, "", huffmanCodes);

        return huffmanCodes.OrderBy(x => x.Value.Length).ToList();
    }

    static void Main() {
        var freq = new Dictionary<char, int> {
            { 'a', 5 }, { 'b', 9 }, { 'c', 12 },
            { 'd', 13 }, { 'e', 16 }, { 'f', 45 }
        };

        var result = HuffmanEncoding(freq);
        Console.WriteLine("Huffman Codes:");
        foreach (var kvp in result) Console.WriteLine($"{kvp.Key}: {kvp.Value}");
    }
}


import heapq

def huffman_encoding(freq):
    heap = [[weight, [char, ""]] for char, weight in freq.items()]
    heapq.heapify(heap)

    while len(heap) > 1:
        lo = heapq.heappop(heap)
        hi = heapq.heappop(heap)
        for pair in lo[1:]:
            pair[1] = '0' + pair[1]
        for pair in hi[1:]:
            pair[1] = '1' + pair[1]
        heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])

    return sorted(heapq.heappop(heap)[1:], key=lambda p: (len(p[-1]), p))

# Example usage
freq = {'a': 5, 'b': 9, 'c': 12, 'd': 13, 'e': 16, 'f': 45}
result = huffman_encoding(freq)
print("Huffman Codes:", result)


import java.util.*;

class HuffmanNode implements Comparable<HuffmanNode> {
    char ch;
    int freq;
    HuffmanNode left, right;

    HuffmanNode(char ch, int freq) {
        this.ch = ch;
        this.freq = freq;
    }

    @Override
    public int compareTo(HuffmanNode other) {
        return this.freq - other.freq;
    }
}

public class HuffmanEncoding {
    public static void generateCodes(HuffmanNode node, String code, Map<Character, String> huffmanCodes) {
        if (node == null) return;
        if (node.ch != '\0') huffmanCodes.put(node.ch, code);
        generateCodes(node.left, code + "0", huffmanCodes);
        generateCodes(node.right, code + "1", huffmanCodes);
    }

    public static List<Map.Entry<Character, String>> huffmanEncoding(Map<Character, Integer> freq) {
        PriorityQueue<HuffmanNode> pq = new PriorityQueue<>();
        for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
            pq.offer(new HuffmanNode(entry.getKey(), entry.getValue()));
        }

        while (pq.size() > 1) {
            HuffmanNode left = pq.poll();
            HuffmanNode right = pq.poll();
            HuffmanNode sum = new HuffmanNode('\0', left.freq + right.freq);
            sum.left = left;
            sum.right = right;
            pq.offer(sum);
        }

        HuffmanNode root = pq.poll();
        Map<Character, String> huffmanCodes = new HashMap<>();
        generateCodes(root, "", huffmanCodes);

        List<Map.Entry<Character, String>> result = new ArrayList<>(huffmanCodes.entrySet());
        result.sort(Comparator.comparingInt(e -> e.getValue().length()));
        return result;
    }

    public static void main(String[] args) {
        Map<Character, Integer> freq = Map.of(
            'a', 5, 'b', 9, 'c', 12,
            'd', 13, 'e', 16, 'f', 45
        );

        List<Map.Entry<Character, String>> result = huffmanEncoding(freq);
        System.out.println("Huffman Codes:");
        for (Map.Entry<Character, String> entry : result) {
            System.out.println(entry.getKey() + ": " + entry.getValue());
        }
    }
}


type Node = {
    char: string | null;
    freq: number;
    left?: Node;
    right?: Node;
};

function generateCodes(node: Node | undefined, code: string, huffmanCodes: Map<string, string>) {
    if (!node) return;
    if (node.char) huffmanCodes.set(node.char, code);
    generateCodes(node.left, code + "0", huffmanCodes);
    generateCodes(node.right, code + "1", huffmanCodes);
}

function huffmanEncoding(freq: Map<string, number>): [string, string][] {
    const heap: Node[] = Array.from(freq.entries()).map(([char, freq]) => ({ char, freq }));

    heap.sort((a, b) => a.freq - b.freq);

    while (heap.length > 1) {
        const left = heap.shift()!;
        const right = heap.shift()!;
        heap.push({
            char: null,
            freq: left.freq + right.freq,
            left,
            right,
        });
        heap.sort((a, b) => a.freq - b.freq);
    }

    const root = heap[0];
    const huffmanCodes = new Map<string, string>();
    generateCodes(root, "", huffmanCodes);

    return Array.from(huffmanCodes.entries()).sort((a, b) => a[1].length - b[1].length);
}

// Example usage
const freq = new Map<string, number>([
    ["a", 5], ["b", 9], ["c", 12],
    ["d", 13], ["e", 16], ["f", 45]
]);

const result = huffmanEncoding(freq);
console.log("Huffman Codes:", result);

Explanation: The binary codes are generated by merging the least frequent nodes until one root remains.

5. N Meetings in One Room

Problem: Schedule the maximum number of meetings in one room.

Approach:

Sort meetings by their end time.
Use a greedy approach similar to the Activity Selection Problem.

Code:


#include <iostream>
#include <vector>
#include <algorithm>

int maxMeetings(std::vector<int>& start, std::vector<int>& end) {
    std::vector<std::pair<int, int>> meetings;
    for (size_t i = 0; i < start.size(); ++i) {
        meetings.push_back({start[i], end[i]});
    }

    std::sort(meetings.begin(), meetings.end(), [](auto& a, auto& b) { return a.second < b.second; });

    int count = 0, last_end = 0;
    for (auto& meeting : meetings) {
        if (meeting.first > last_end) {
            ++count;
            last_end = meeting.second;
        }
    }
    return count;
}

int main() {
    std::vector<int> start = {1, 3, 0, 5, 8, 5};
    std::vector<int> end = {2, 4, 6, 7, 9, 9};
    std::cout << "Maximum meetings: " << maxMeetings(start, end) << std::endl;
    return 0;
}


using System;
using System.Collections.Generic;
using System.Linq;

class Program {
    static int MaxMeetings(List<int> start, List<int> end) {
        var meetings = start.Zip(end, (s, e) => new { Start = s, End = e }).OrderBy(m => m.End).ToList();
        int count = 0, lastEnd = 0;

        foreach (var meeting in meetings) {
            if (meeting.Start > lastEnd) {
                count++;
                lastEnd = meeting.End;
            }
        }
        return count;
    }

    static void Main() {
        var start = new List<int> {1, 3, 0, 5, 8, 5};
        var end = new List<int> {2, 4, 6, 7, 9, 9};
        Console.WriteLine("Maximum meetings: " + MaxMeetings(start, end));
    }
}


def max_meetings(start, end):
    meetings = list(zip(start, end))
    meetings.sort(key=lambda x: x[1])

    count = 0
    last_end = 0
    for s, e in meetings:
        if s > last_end:
            count += 1
            last_end = e

    return count

start = [1, 3, 0, 5, 8, 5]
end = [2, 4, 6, 7, 9, 9]
result = max_meetings(start, end)
print("Maximum meetings:", result)


import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;

class Meeting {
    int start, end;

    Meeting(int start, int end) {
        this.start = start;
        this.end = end;
    }
}

public class Main {
    static int maxMeetings(List<Integer> start, List<Integer> end) {
        List<Meeting> meetings = new ArrayList<>();
        for (int i = 0; i < start.size(); i++) {
            meetings.add(new Meeting(start.get(i), end.get(i)));
        }

        meetings.sort(Comparator.comparingInt(m -> m.end));

        int count = 0, lastEnd = 0;
        for (Meeting meeting : meetings) {
            if (meeting.start > lastEnd) {
                count++;
                lastEnd = meeting.end;
            }
        }
        return count;
    }

    public static void main(String[] args) {
        List<Integer> start = List.of(1, 3, 0, 5, 8, 5);
        List<Integer> end = List.of(2, 4, 6, 7, 9, 9);
        System.out.println("Maximum meetings: " + maxMeetings(start, end));
    }
}


function maxMeetings(start: number[], end: number[]): number {
    const meetings = start.map((s, i) => ({ start: s, end: end[i] }));
    meetings.sort((a, b) => a.end - b.end);

    let count = 0, lastEnd = 0;
    for (const meeting of meetings) {
        if (meeting.start > lastEnd) {
            count++;
            lastEnd = meeting.end;
        }
    }
    return count;
}

const start = [1, 3, 0, 5, 8, 5];
const end = [2, 4, 6, 7, 9, 9];
console.log("Maximum meetings:", maxMeetings(start, end));

Explanation: The sorting by end time ensures optimal use of the room without overlaps.

Medium Problems on Greedy Algorithm

1. Job Sequencing Problem

Problem: Given jobs with deadlines and profits, schedule jobs to maximize total profit while ensuring no two jobs overlap beyond their deadlines.

Approach:

Sort jobs by profit in descending order.
Assign each job to the latest available slot before its deadline, if possible.

Code:


#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Job {
    int deadline, profit;
};

bool compare(Job a, Job b) {
    return a.profit > b.profit;
}

int job_sequencing(vector<Job>& jobs) {
    sort(jobs.begin(), jobs.end(), compare);

    int n = 0;
    for (auto& job : jobs) {
        n = max(n, job.deadline);
    }

    vector<int> time_slots(n, -1);
    int total_profit = 0;

    for (auto& job : jobs) {
        for (int t = min(n, job.deadline) - 1; t >= 0; t--) {
            if (time_slots[t] == -1) {
                time_slots[t] = job.profit;
                total_profit += job.profit;
                break;
            }
        }
    }

    return total_profit;
}

int main() {
    vector<Job> jobs = {{2, 100}, {1, 50}, {2, 10}, {1, 20}};
    cout << "Maximum Profit: " << job_sequencing(jobs) << endl;
    return 0;
}


using System;
using System.Linq;

public class Job {
    public int Deadline, Profit;
}

class Program {
    static int JobSequencing(Job[] jobs) {
        var sortedJobs = jobs.OrderByDescending(job => job.Profit).ToArray();

        int n = sortedJobs.Max(job => job.Deadline);
        int[] timeSlots = new int[n];
        Array.Fill(timeSlots, -1);
        int totalProfit = 0;

        foreach (var job in sortedJobs) {
            for (int t = Math.Min(n, job.Deadline) - 1; t >= 0; t--) {
                if (timeSlots[t] == -1) {
                    timeSlots[t] = job.Profit;
                    totalProfit += job.Profit;
                    break;
                }
            }
        }

        return totalProfit;
    }

    static void Main() {
        var jobs = new Job[] {
            new Job { Deadline = 2, Profit = 100 },
            new Job { Deadline = 1, Profit = 50 },
            new Job { Deadline = 2, Profit = 10 },
            new Job { Deadline = 1, Profit = 20 }
        };
        
        Console.WriteLine("Maximum Profit: " + JobSequencing(jobs));
    }
}


def job_sequencing(jobs):
    jobs.sort(key=lambda x: x[1], reverse=True)

    n = max(job[0] for job in jobs)
    time_slots = [-1] * n
    total_profit = 0

    for deadline, profit in jobs:
        for t in range(min(n, deadline) - 1, -1, -1):
            if time_slots[t] == -1:
                time_slots[t] = profit
                total_profit += profit
                break

    return total_profit

# Example usage
jobs = [(2, 100), (1, 50), (2, 10), (1, 20)]
result = job_sequencing(jobs)
print("Maximum Profit:", result)


import java.util.*;

class Job {
    int deadline, profit;

    Job(int deadline, int profit) {
        this.deadline = deadline;
        this.profit = profit;
    }
}

public class Main {
    public static int jobSequencing(List<Job> jobs) {
        jobs.sort((a, b) -> b.profit - a.profit);

        int n = jobs.stream().mapToInt(job -> job.deadline).max().getAsInt();
        int[] timeSlots = new int[n];
        Arrays.fill(timeSlots, -1);
        int totalProfit = 0;

        for (Job job : jobs) {
            for (int t = Math.min(n, job.deadline) - 1; t >= 0; t--) {
                if (timeSlots[t] == -1) {
                    timeSlots[t] = job.profit;
                    totalProfit += job.profit;
                    break;
                }
            }
        }

        return totalProfit;
    }

    public static void main(String[] args) {
        List<Job> jobs = Arrays.asList(
            new Job(2, 100),
            new Job(1, 50),
            new Job(2, 10),
            new Job(1, 20)
        );

        System.out.println("Maximum Profit: " + jobSequencing(jobs));
    }
}


function jobSequencing(jobs: [number, number][]): number {
    jobs.sort((a, b) => b[1] - a[1]);

    const n = Math.max(...jobs.map(job => job[0]));
    const timeSlots = Array(n).fill(-1);
    let totalProfit = 0;

    for (const [deadline, profit] of jobs) {
        for (let t = Math.min(n, deadline) - 1; t >= 0; t--) {
            if (timeSlots[t] === -1) {
                timeSlots[t] = profit;
                totalProfit += profit;
                break;
            }
        }
    }

    return totalProfit;
}

const jobs: [number, number][] = [
    [2, 100], [1, 50], [2, 10], [1, 20]
];

console.log("Maximum Profit:", jobSequencing(jobs));

2. Candy Distribution Problem

Problem: Distribute candies to children such that children with higher ratings get more candies than their neighbors.

Approach:

Traverse the rating array twice (left-to-right and right-to-left) to ensure conditions are met.

Code:


#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int candy_distribution(vector<int>& ratings) {
    int n = ratings.size();
    vector<int> candies(n, 1);

    // Left to right
    for (int i = 1; i < n; i++) {
        if (ratings[i] > ratings[i - 1]) {
            candies[i] = candies[i - 1] + 1;
        }
    }

    // Right to left
    for (int i = n - 2; i >= 0; i--) {
        if (ratings[i] > ratings[i + 1]) {
            candies[i] = max(candies[i], candies[i + 1] + 1);
        }
    }

    int result = 0;
    for (int candy : candies) {
        result += candy;
    }

    return result;
}

int main() {
    vector<int> ratings = {1, 0, 2};
    cout << "Minimum Candies: " << candy_distribution(ratings) << endl;
    return 0;
}


using System;

class Program
{
    public static int CandyDistribution(int[] ratings)
    {
        int n = ratings.Length;
        int[] candies = new int[n];
        for (int i = 0; i < n; i++)
        {
            candies[i] = 1;
        }

        // Left to right
        for (int i = 1; i < n; i++)
        {
            if (ratings[i] > ratings[i - 1])
            {
                candies[i] = candies[i - 1] + 1;
            }
        }

        // Right to left
        for (int i = n - 2; i >= 0; i--)
        {
            if (ratings[i] > ratings[i + 1])
            {
                candies[i] = Math.Max(candies[i], candies[i + 1] + 1);
            }
        }

        int result = 0;
        foreach (int candy in candies)
        {
            result += candy;
        }

        return result;
    }

    static void Main()
    {
        int[] ratings = { 1, 0, 2 };
        Console.WriteLine("Minimum Candies: " + CandyDistribution(ratings));
    }
}


def candy_distribution(ratings):
    n = len(ratings)
    candies = [1] * n

    # Left to right
    for i in range(1, n):
        if ratings[i] > ratings[i - 1]:
            candies[i] = candies[i - 1] + 1

    # Right to left
    for i in range(n - 2, -1, -1):
        if ratings[i] > ratings[i + 1]:
            candies[i] = max(candies[i], candies[i + 1] + 1)

    return sum(candies)

# Example usage
ratings = [1, 0, 2]
result = candy_distribution(ratings)
print("Minimum Candies:", result)


public class Main {
    public static int candyDistribution(int[] ratings) {
        int n = ratings.length;
        int[] candies = new int[n];
        for (int i = 0; i < n; i++) {
            candies[i] = 1;
        }

        // Left to right
        for (int i = 1; i < n; i++) {
            if (ratings[i] > ratings[i - 1]) {
                candies[i] = candies[i - 1] + 1;
            }
        }

        // Right to left
        for (int i = n - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                candies[i] = Math.max(candies[i], candies[i + 1] + 1);
            }
        }

        int result = 0;
        for (int candy : candies) {
            result += candy;
        }

        return result;
    }

    public static void main(String[] args) {
        int[] ratings = {1, 0, 2};
        System.out.println("Minimum Candies: " + candyDistribution(ratings));
    }
}


function candyDistribution(ratings: number[]): number {
    const n = ratings.length;
    const candies: number[] = new Array(n).fill(1);

    // Left to right
    for (let i = 1; i < n; i++) {
        if (ratings[i] > ratings[i - 1]) {
            candies[i] = candies[i - 1] + 1;
        }
    }

    // Right to left
    for (let i = n - 2; i >= 0; i--) {
        if (ratings[i] > ratings[i + 1]) {
            candies[i] = Math.max(candies[i], candies[i + 1] + 1);
        }
    }

    return candies.reduce((acc, val) => acc + val, 0);
}

// Example usage
const ratings = [1, 0, 2];
const result = candyDistribution(ratings);
console.log("Minimum Candies:", result);

Hard Problem on Greedy Algorithm

Minimum Platforms

Problem: Given the arrival and departure times of trains, find the minimum number of platforms required.

Approach:

Sort arrival and departure times.
Use a greedy approach with two-pointers.

Code:


#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int min_platforms(vector<int>& arrival, vector<int>& departure) {
    sort(arrival.begin(), arrival.end());
    sort(departure.begin(), departure.end());

    int n = arrival.size();
    int platforms = 0, max_platforms = 0;
    int i = 0, j = 0;

    while (i < n && j < n) {
        if (arrival[i] < departure[j]) {
            platforms++;
            max_platforms = max(max_platforms, platforms);
            i++;
        } else {
            platforms--;
            j++;
        }
    }
    return max_platforms;
}

int main() {
    vector<int> arrival = {900, 940, 950, 1100, 1500, 1800};
    vector<int> departure = {910, 1200, 1120, 1130, 1900, 2000};
    cout << "Minimum Platforms Required: " << min_platforms(arrival, departure) << endl;
    return 0;
}


using System;
using System.Linq;

class Program {
    static int MinPlatforms(int[] arrival, int[] departure) {
        Array.Sort(arrival);
        Array.Sort(departure);

        int n = arrival.Length;
        int platforms = 0, maxPlatforms = 0;
        int i = 0, j = 0;

        while (i < n && j < n) {
            if (arrival[i] < departure[j]) {
                platforms++;
                maxPlatforms = Math.Max(maxPlatforms, platforms);
                i++;
            } else {
                platforms--;
                j++;
            }
        }
        return maxPlatforms;
    }

    static void Main() {
        int[] arrival = {900, 940, 950, 1100, 1500, 1800};
        int[] departure = {910, 1200, 1120, 1130, 1900, 2000};
        Console.WriteLine("Minimum Platforms Required: " + MinPlatforms(arrival, departure));
    }
}


def min_platforms(arrival, departure):
    arrival.sort()
    departure.sort()

    n = len(arrival)
    platforms = 0
    max_platforms = 0
    i = 0
    j = 0

    while i < n and j < n:
        if arrival[i] < departure[j]:
            platforms += 1
            max_platforms = max(max_platforms, platforms)
            i += 1
        else:
            platforms -= 1
            j += 1

    return max_platforms

# Example usage
arrival = [900, 940, 950, 1100, 1500, 1800]
departure = [910, 1200, 1120, 1130, 1900, 2000]
print("Minimum Platforms Required:", min_platforms(arrival, departure))


import java.util.Arrays;

public class Main {
    public static int minPlatforms(int[] arrival, int[] departure) {
        Arrays.sort(arrival);
        Arrays.sort(departure);

        int n = arrival.length;
        int platforms = 0, maxPlatforms = 0;
        int i = 0, j = 0;

        while (i < n && j < n) {
            if (arrival[i] < departure[j]) {
                platforms++;
                maxPlatforms = Math.max(maxPlatforms, platforms);
                i++;
            } else {
                platforms--;
                j++;
            }
        }
        return maxPlatforms;
    }

    public static void main(String[] args) {
        int[] arrival = {900, 940, 950, 1100, 1500, 1800};
        int[] departure = {910, 1200, 1120, 1130, 1900, 2000};
        System.out.println("Minimum Platforms Required: " + minPlatforms(arrival, departure));
    }
}


function minPlatforms(arrival: number[], departure: number[]): number {
    arrival.sort((a, b) => a - b);
    departure.sort((a, b) => a - b);

    let n = arrival.length;
    let platforms = 0;
    let maxPlatforms = 0;
    let i = 0;
    let j = 0;

    while (i < n && j < n) {
        if (arrival[i] < departure[j]) {
            platforms++;
            maxPlatforms = Math.max(maxPlatforms, platforms);
            i++;
        } else {
            platforms--;
            j++;
        }
    }

    return maxPlatforms;
}

// Example usage
const arrival = [900, 940, 950, 1100, 1500, 1800];
const departure = [910, 1200, 1120, 1130, 1900, 2000];
console.log("Minimum Platforms Required:", minPlatforms(arrival, departure));

More Practice with the Below Articles:

Selection Sort
Knapsack Problem
Minimum Spanning Tree
Single-Source Shortest Path Problem
Job Scheduling Problem
Prim's Minimal Spanning Tree Algorithm
Kruskal's Minimal Spanning Tree Algorithm
Dijkstra's Minimal Spanning Tree Algorithm
Huffman Coding
Ford-Fulkerson Algorithm

Real World Applications of Greedy Algorithm

1. Job Scheduling Problem- Greedy algorithms are used in job sequencing and scheduling where tasks are assigned to machines or time slots to maximize profit or minimize deadline violations.

Greedy algorithm applications in job scheduling

Used in CPU task scheduling, project management, and operating systems.

2. Huffman Coding (Data Compression)- Greedy approach is applied in Huffman Coding to assign variable-length codes to input characters based on frequency, reducing total encoding size.

Greedy algorithm in huffman coding

Used in file compression tools (ZIP), multimedia formats (MP3, JPEG), and data transmission.

Advantages of Greedy Algorithm

1. Simplicity and Ease of Implementation- Greedy algorithms are simple and intuitive. Their logic is easy to follow, making them ideal for beginners and for problems that don’t require complex solutions. Developers can quickly design and implement them with minimal effort.

2. Faster Execution Time- Greedy algorithms are highly efficient in terms of time complexity. Since they make one decision at a time without backtracking, they run faster than exhaustive methods like brute-force or dynamic programming.

3. Memory Efficiency- One of the biggest advantages is low memory usage. Greedy algorithms don’t store all possible solutions or states. Instead, they only maintain the current best solution, making them suitable for memory-constrained systems.

4. Optimal or Near-Optimal Solutions- For many problems, greedy algorithms deliver optimal or close-to-optimal results. They are ideal for solving real-world optimization problems like:

Activity Selection
Fractional Knapsack
Huffman Coding

5. No Backtracking or Recalculation- Once a decision is made, it is final and not revisited. This feature simplifies the logic and eliminates the need for complex recursion or recalculations.

When Not to use greedy algorithm

While greedy algorithms are fast and easy to implement, they are not suitable for every type of problem. There are specific scenarios where the greedy approach fails to deliver the correct or optimal solution.

1. When the Problem Lacks the Greedy-Choice Property

Greedy algorithms work only when a globally optimal solution can be built by making locally optimal choices.

If the problem does not have the greedy-choice property, the greedy method will likely produce an incorrect or suboptimal result.

Example: In the 0/1 Knapsack Problem, choosing the item with the highest value-to-weight ratio may not lead to the best total value.

2. When the Problem Doesn’t Have Optimal Substructure

For a greedy algorithm to be effective, optimal substructure must exist—meaning the optimal solution to the whole problem must include optimal solutions to its subproblems.

If the problem depends on multiple subproblem combinations (like overlapping subproblems), you should use Dynamic Programming instead.

Example: Longest Common Subsequence (LCS) cannot be solved using greedy methods because it requires exploring multiple paths.

3. When Backtracking is Required

Greedy algorithms do not backtrack or reconsider decisions. If a problem requires trying multiple combinations or undoing a choice to find the correct path, Backtracking is a better option.

Example: In N-Queens Problem, greedy choice may fail to find a solution; backtracking is needed to explore different arrangements.

4. When Accuracy is More Important than Speed

Greedy algorithms prioritize speed and simplicity, often at the cost of accuracy. If your application requires precise, guaranteed-optimal solutions, avoid greedy methods.

Example: Graph coloring, Travelling Salesman Problem (TSP) – greedy solutions often fail to find the optimal result.

5. When Problem Has Complex Dependencies

Greedy algorithms are not ideal for problems where future decisions depend on previous ones in non-trivial ways. Such dependencies often require Dynamic Programming to manage overlapping subproblems and track multiple states.

Disadvantages of Greedy Algorithm

Greedy algorithms are widely appreciated for their speed and simplicity, but they are not suitable for every problem. Below are the major limitations and drawbacks of the greedy approach:

1. Lack of Global Optimization- Greedy algorithms focus on making the best local choice at each step without considering the overall context of the problem. As a result, they often fail to produce the globally optimal solution.

2. No Backtracking or Re-Evaluation- Once a greedy algorithm makes a decision, it does not reconsider it, even if a better option appears later. This lack of backtracking can cause the algorithm to get stuck with poor decisions that affect the final result.

3. Depends Heavily on Problem Structure- Greedy algorithms work only when the problem satisfies two essential properties:

Greedy-choice property
Optimal substructure
If these properties are not present, the greedy approach will likely fail or return incorrect results.

4. Limited Problem-Solving Scope- Greedy algorithms are not universally applicable. They work well for problems like:

Huffman Coding
Fractional Knapsack
Activity Selection

But they often fail in complex problems such as:

0/1 Knapsack Problem
Travelling Salesman Problem
Graph coloring

5. May Lead to Approximate, Not Exact Solutions- In some cases, the greedy approach only provides a near-optimal or approximate solution, not the exact best one. This can be acceptable in real-time systems but unsuitable for applications requiring precise answers.

6. Hard to Prove Correctness- Even though greedy algorithms are easy to implement, it is often mathematically challenging to prove their correctness. Ensuring that a greedy solution is always optimal requires in-depth analysis, which is not always straightforward.

7. Inflexibility in Changing Requirements- If the problem requirements or inputs change dynamically, greedy algorithms may not adapt well, unlike dynamic programming or recursive approaches that can handle more complex variations.

Summary

Hence, we have covered all the concepts of greedy algorithms, their characteristics, advantages, disadvantages, types, and examples. A greedy algorithm does not always lead to the global optimal solution. All problems that can be solved using a greedy approach exhibit greedy choice and optimal substructure properties. To test your understanding of the concepts of the greedy approach, enroll in our Best Free Dsa Course.