Hashing in Data Structures: Types and Functions [With Examples]

Hash Function in Data Structures: An Overview

In this DSA tutorial, we will endeavor to unravel key hashing concepts, shedding light on its vital role and why it has emerged as a go-to technique for efficiently managing extensive datasets within the realm of the Dsa Course Online

What is Hashing in Data Structures?

Data can be hashed into a shorter, fixed-length value for quicker access using a key or set of characters. This is how key-value pairs are stored in hash tables. The representation of the hash function looks like this:

 hash=hashfunc(key)

How does Hashing in Data Structures Work?

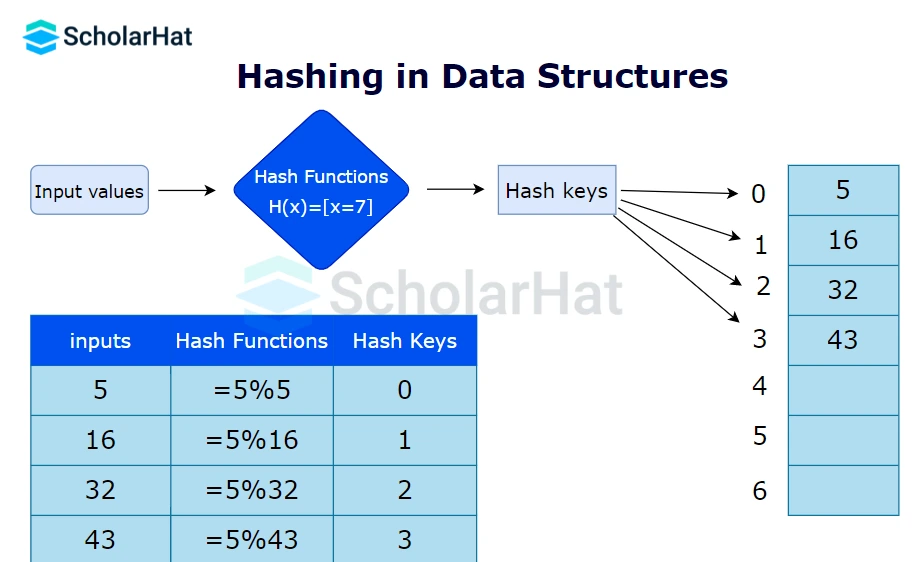
• Hash key: It is the data you want to be hashed in the hash table. The hashing algorithm translates the key to the hash value. This identifier can be a string or an integer. There are some types of hash keys:
  1. Public key - It is an open key used solely for data encryption.
  2. Private key - It is known as a symmetric key used for both purposes, encryption and decryption.
  3. SSH public key - SSH is a set of both public and private keys.
• Hash Function: It performs the mathematical operation of accepting the key value as input and producing the hash code or hash value as the output. Some of the characteristics of an ideal hash function are as follows:
  • It must produce the same hash value for the same hash key to be deterministic.
  • Every input has a unique hash code. This feature is known as the hash property.
  • It must be collision-friendly.
  • A little bit of change leads to a drastic change in the output.
  • The calculation must be quick
• Hash Table: It is a type of data structure that stores data in an array format. The table maps keys to values using a hash function.

Read More - Data Structure Interview Questions for Experienced

Use cases of Hashing In DSA

• Password Storage: Hash functions are commonly used to securely store passwords. Instead of storing the actual passwords, the system stores their hash values. When a user enters a password, it is hashed and compared with the stored hash value for authentication.
• Data Integrity: Hashing is used to ensure data integrity by generating hash values for files or messages. By comparing the hash values before and after transmission or storage, it's possible to detect if any changes or tampering occurred.
• Data Retrieval: Hashing is used in data structures like hash tables, which provide efficient data retrieval based on key-value pairs. The hash value serves as an index to store and retrieve data quickly.
• Digital Signatures: Hash functions are an integral part of digital signatures. They are used to generate a unique hash value for a message, which is then encrypted with the signer's private key. This allows for verification of the authenticity and integrity of the message using the signer's public key.

Example of Hashing

import hashlib

def sha256(input):
    hash_object = hashlib.sha256(input.encode('utf-8'))
    hex_digest = hash_object.hexdigest()
    return hex_digest

def main():
    message = "Hello, world!"
    hash_value = sha256(message)
    
    print("Message: " + message)
    print("SHA-256 Hash: " + hash_value)

if __name__ == "__main__":
    main()
    

import java.nio.charset.StandardCharsets;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;

public class Main {

    public static void main(String[] args) {
        String message = "Hello, world!";
        String hashValue = sha256(message);

        System.out.println("Message: " + message);
        System.out.println("SHA-256 Hash: " + hashValue);
    }

    public static String sha256(String input) {
        try {
            MessageDigest digest = MessageDigest.getInstance("SHA-256");
            byte[] hash = digest.digest(input.getBytes(StandardCharsets.UTF_8));

            StringBuilder hexDigest = new StringBuilder();

            for (byte b : hash) {
                String hex = String.format("%02x", b);
                hexDigest.append(hex);
            }

            return hexDigest.toString();

        } catch (NoSuchAlgorithmException e) {
            e.printStackTrace();
            return null;
        }
    }
}
    

#include <iostream>
#include <iomanip>
#include <sstream>
#include <openssl/sha.h>

std::string sha256(const std::string &input) {
    unsigned char hash[SHA256_DIGEST_LENGTH];
    SHA256_CTX sha256;
    
    SHA256_Init(&sha256);
    SHA256_Update(&sha256, input.c_str(), input.size());
    SHA256_Final(hash, &sha256);
    
    std::stringstream ss;
    for (int i = 0; i < SHA256_DIGEST_LENGTH; i++) {
        ss << std::hex << std::setw(2) << std::setfill('0') << static_cast(hash[i]);
    }
    
    return ss.str();
}

int main() {
    std::string message = "Hello, world!";
    std::string hashValue = sha256(message);
    
    std::cout << "Message: " << message << std::endl;
    std::cout << "SHA-256 Hash: " << hashValue << std::endl;
    
    return 0;
}
    

Output

Message: Hello, world!
SHA-256 Hash: 315f5bdb76d078c43b8ac0064e4a0164612b1fce77c869345bfc94c75894edd3 

Types of Hash Functions

1. Division Method.
2. Mid Square Method.
3. Folding Method.
4. Multiplication Method.

1. Division Method

Formula:

h(K) = k mod M

(where k = key value and M = the size of the hash table)

Advantages:

• This method is effective for all values of M.
• The division strategy only requires one operation, thus it is quite quick.

Disadvantages:

• Since the hash table maps consecutive keys to successive hash values, this could result in poor performance.
• There are times when exercising extra caution while selecting M's value is necessary.

Example of Division Method

k = 1987
M = 13h(1987) = 1987 mod 13
h(1987) = 4 

2. Mid Square Method

The following steps are required to calculate this hash method:

• k*k, or square the value of k
• Using the middle r digits, calculate the hash value.

Formula:

h(K) = h(k x k)

(where k = key value)

Advantages:

• This technique works well because most or all of the digits in the key value affect the result. All of the necessary digits participate in a process that results in the middle digits of the squared result.
• The result is not dominated by the top or bottom digits of the initial key value.

Disadvantages:

• The size of the key is one of the limitations of this system; if the key is large, its square will contain twice as many digits.
• Probability of collisions occurring repeatedly.

Example of Mid Square Method

k = 60Therefore,k = k x k
k = 60 x 60
k = 3600Thus, 
h(60) = 60    

3. Folding Method

The process involves two steps:

• except for the last component, which may have fewer digits than the other parts, the key-value k should be divided into a predetermined number of pieces, such as k1, k2, k3,..., kn, each having the same amount of digits.
• Add each element individually. The hash value is calculated without taking into account the final carry, if any.

Formula:

k = k1, k2, k3, k4, ….., kn

s = k1+ k2 + k3 + k4 +….+ kn

h(K)= s

(Where, s = addition of the parts of key k)

Advantages:

• Creates a simple hash value by precisely splitting the key value into equal-sized segments.
• Without regard to distribution in a hash table.

Disadvantages:

• When there are too many collisions, efficiency can occasionally suffer.

Example of Folding Method

k = 12345
k1 = 67; k2 = 89; k3 = 12Therefore,s = k1 + k2 + k3
s = 67 + 89 + 12
s = 168 

4. Multiplication Method

• Determine a constant value. A, where (0, A, 1)
• Add A to the key value and multiply.
• Consider kA's fractional portion.
• Multiply the outcome of the preceding step by M, the hash table's size.

Formula:

h(K) = floor (M (kA mod 1))

(Where, M = size of the hash table, k = key value and A = constant value)

Advantages:

• Any number between 0 and 1 can be applied to it, however, some values seem to yield better outcomes than others.

Disadvantages:

• The multiplication method is often appropriate when the table size is a power of two since multiplication hashing makes it possible to quickly compute the index by key.

Example of Multiplication Method

k = 5678
A = 0.6829
M = 200
Now, calculating the new value of h(5678):h(5678) = floor[200(5678 x 0.6829 mod 1)]
h(5678) = floor[200(3881.5702 mod 1)]
h(5678) = floor[200(0.5702)]
h(5678) = floor[114.04]
h(5678) = 114
So, with the updated values, h(5678) is 114.  

What is a Hash Collision?

Collision Resolution Techniques in Data Structures

1. Open hashing/separate chaining/closed addressing
2. Open addressing/closed hashing

1. Open hashing/separate chaining/closed addressing

A typical collision handling technique called "separate chaining" links components with the same hash using linked lists. It is also known as closed addressing and employs arrays of linked lists to successfully prevent hash collisions.

Advantages:

• Implementation is simple and easy
• We can add more keys to the table because the hash table has a lot of empty places.
• Less sensitive than average to changing load factors
• Typically utilized when there is uncertainty on the number and frequency of keys to be used in the hash table.

Disadvantages:

• Space is wasted
• The length of the chain lengthens the search period.
• Comparatively worse cache performance to closed hashing.

2. Closed hashing (Open addressing)

1. Linear Probing

Linear probing includes inspecting the hash table sequentially from the very beginning. If the site requested is already occupied, a different one is searched. The distance between probes in linear probing is typically fixed (often set to a value of 1).

Formula

index = key % hashTableSize

Sequence

index = ( hash(n) % T) 
(hash(n) + 1) % T 
(hash(n) + 2) % T 
(hash(n) + 3) % T … and so on.

2. Quadratic Probing

The distance between subsequent probes or entry slots is the only difference between linear and quadratic probing. You must begin traversing until you find an available hashed index slot for an entry record if the slot is already taken. By adding each succeeding value of any arbitrary polynomial in the original hashed index, the distance between slots is determined.

Formula

index = index % hashTableSize

Sequence

index = ( hash(n) % T) 
(hash(n) + 1 x 1) % T 
(hash(n) + 2 x 2) % T 
(hash(n) + 3 x 3) % T … and so on

3. Double-Hashing

The time between probes is determined by yet another hash function. Double hashing is an optimized technique for decreasing clustering. The increments for the probing sequence are computed using an extra hash function.

Formula

(first hash(key) + i * secondHash(key)) % size of the table

Sequence

index = hash(x) % S 
(hash(x) + 1*hash2(x)) % S 
(hash(x) + 2*hash2(x)) % S 
(hash(x) + 3*hash2(x)) % S … and so on

Importance of Hashing

1. Easy retrieval of required information from large data sets in an efficient manner.
2. The hash code produced by the hash function serves as the unique identifier in the data set thus maintaining data integrity.
3. The data is stored in a structured manner as there is an index for every record in the hash table. This ensures efficient storage and retrieval.

Limitations of Hashing

1. Many a time there leads to a situation of collision where two or more inputs have the same hash value.
2. The performance of the hashing algorithm depends upon the quality of the hash function. Sometimes, a not well-thought-of hash function may lead to collisions thus reducing the efficiency of the algorithm.

Summary

To further enhance your knowledge of hashing and other fundamental DSA concepts, enroll in a Free DSA Course with Certificate. This course is designed to provide a comprehensive understanding of data structures and algorithms, equipping you with the skills needed to excel in technical interviews and real-world problem-solving.