Heap in Data Structures

Heap in Data Structures: An Overview

We have learned balanced and complete binary trees in the Binary Trees in Data Structures. Heap Data Structure is a special case of the balanced binary tree where the root node's key is compared with its children and arranged accordingly. In this DSA tutorial, we will see a heap in detail learning about its features, working, types, etc.

To further enhance your understanding and application of heap concepts, consider enrolling in the Dsa Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is a Heap in Data Structures?

A heap is a tree-like data structure in which the tree is a complete binary tree that satisfies the heap property. According to the heap property, all the children of a given node must be greater than the parent node, or all the children must be smaller than the parent node. This type of data structure is also called a binary heap.

Types of Heap Data Structure

There are two main types of heap data structures:

1. Max Heap: In this, all the nodes (including the root) are greater than their respective child nodes. The key of the root node is always the largest among all other nodes.

   

2. Min Heap: In this, all the nodes (including the root) are smaller than their respective child nodes. The key of the root node is always the smallest among all other nodes.

   

Read More - DSA Interview Questions and Answers

Heap Operations in Data Structures

1. Heapify

Heapify is the process of rearranging the elements to form a binary tree that maintains the properties of the heap data structure. After inserting the elements into a heap, they may or may not satisfy the heap properties. In that case, we need to rearrange the locations of the elements in the erroneous heap to make it a heap again. It is used to create a Min-Heap or a Max-Heap.

Algorithm to Heapify a Binary Tree

Heapify(array, size, i)
  set i as largest
  leftChild = 2i + 1
  rightChild = 2i + 2
  
  if leftChild > array[largest]
    set leftChildIndex as largest
  if rightChild > array[largest]
    set rightChildIndex as largest

  swap array[i] and array[largest]

Visualization of the Heapify Operation on a Binary Tree

1. Let the input array be

   

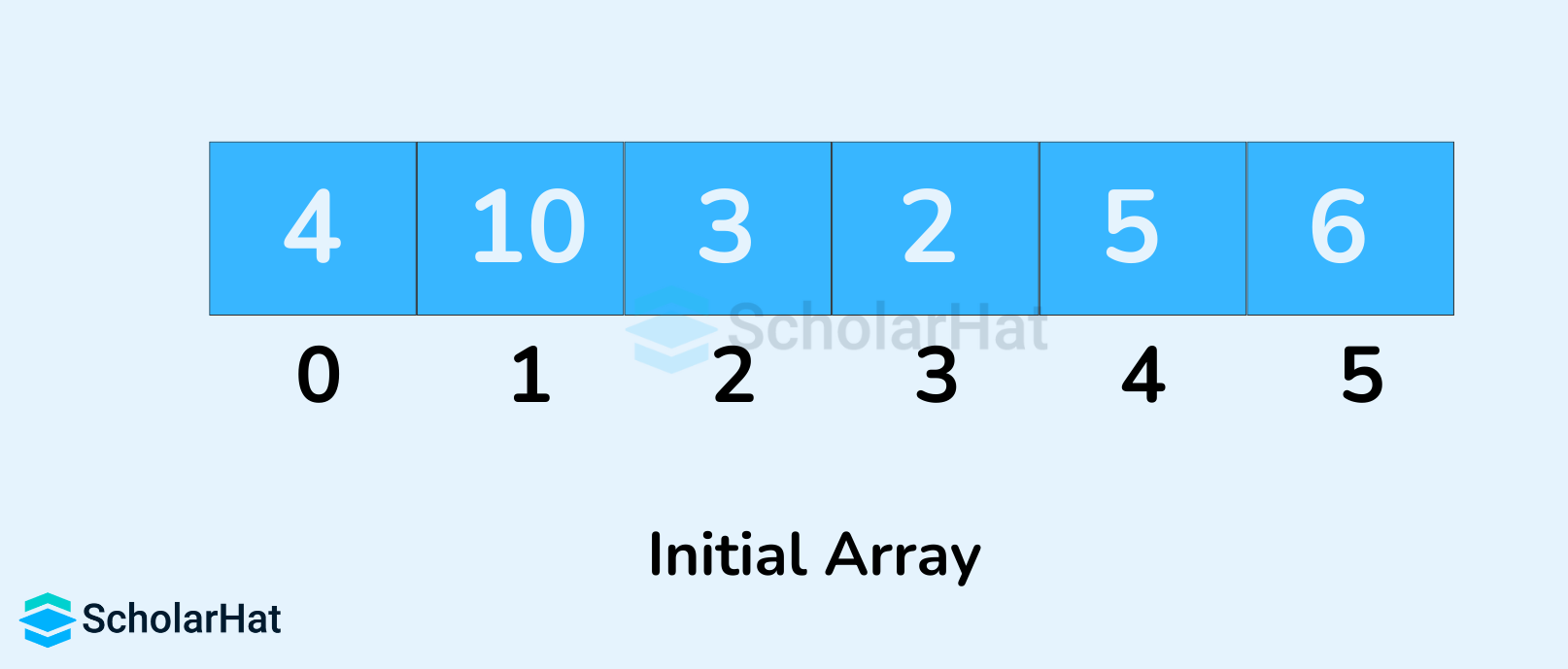
2. Create a complete binary tree from the array

   

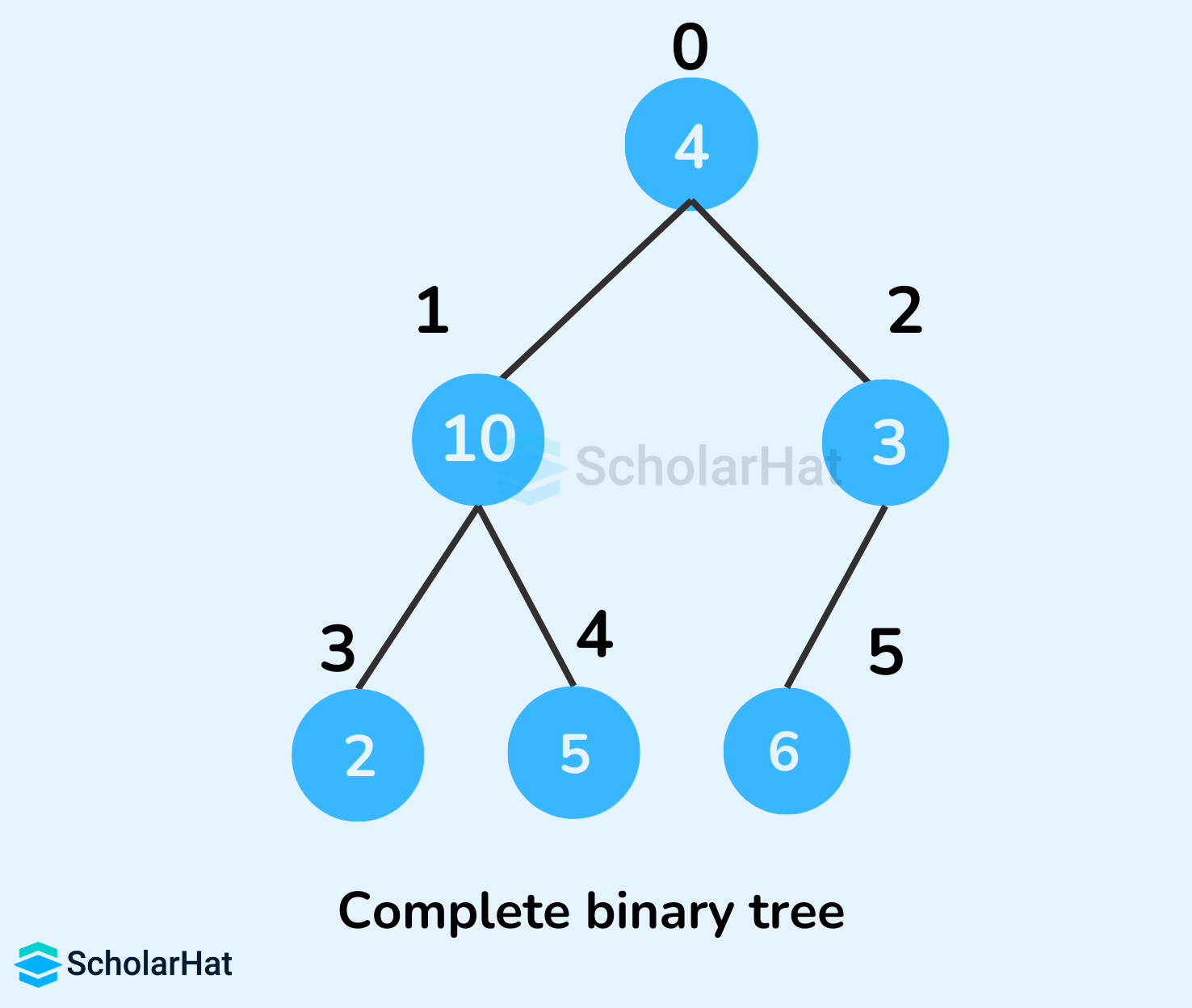
3. Start from the first index of the non-leaf node whose index is given by n/2 - 1.

   

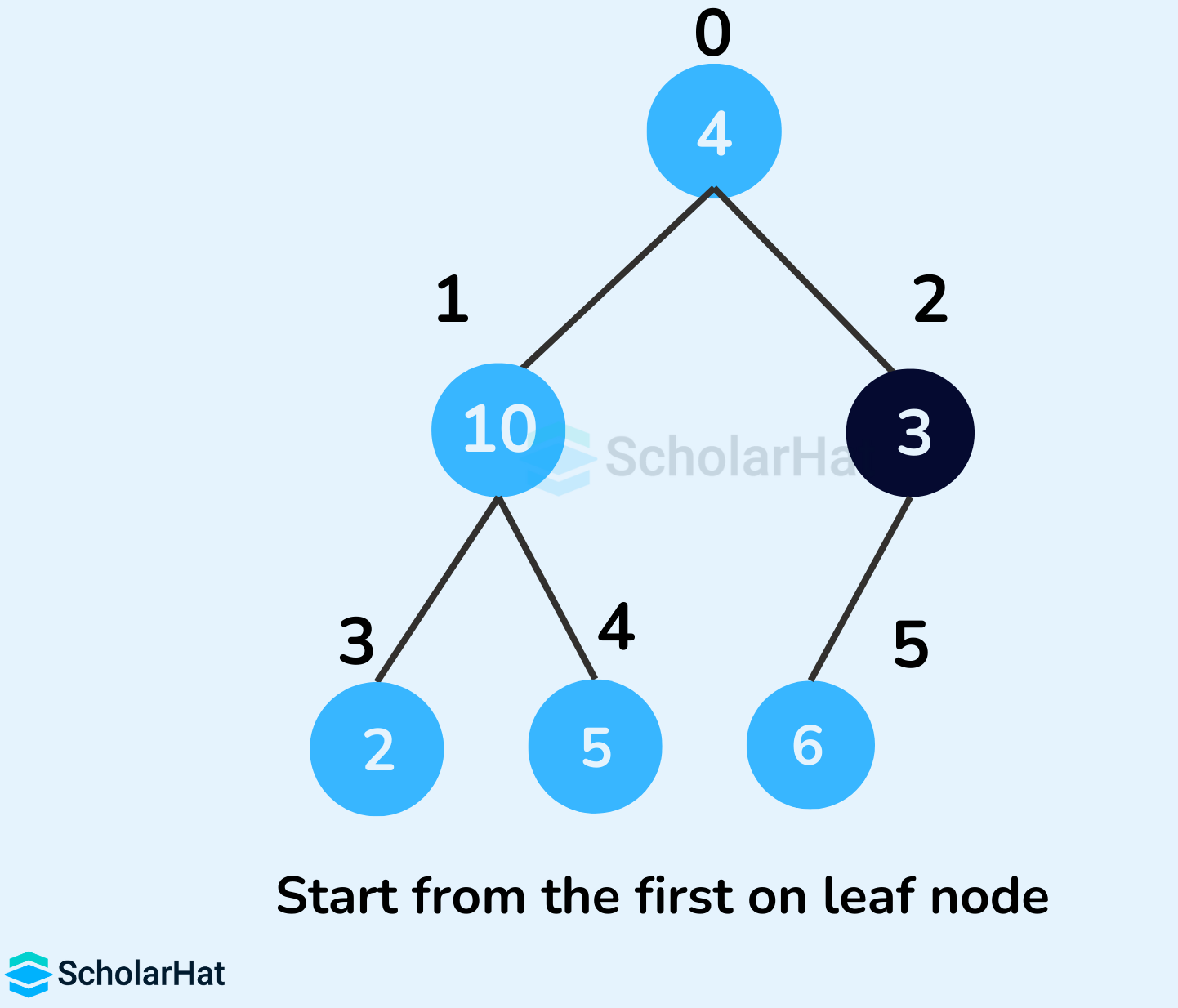
4. Set current element i as largest.
5. The index of the left child is given by 2i + 1 and the right child is given by 2i + 2.
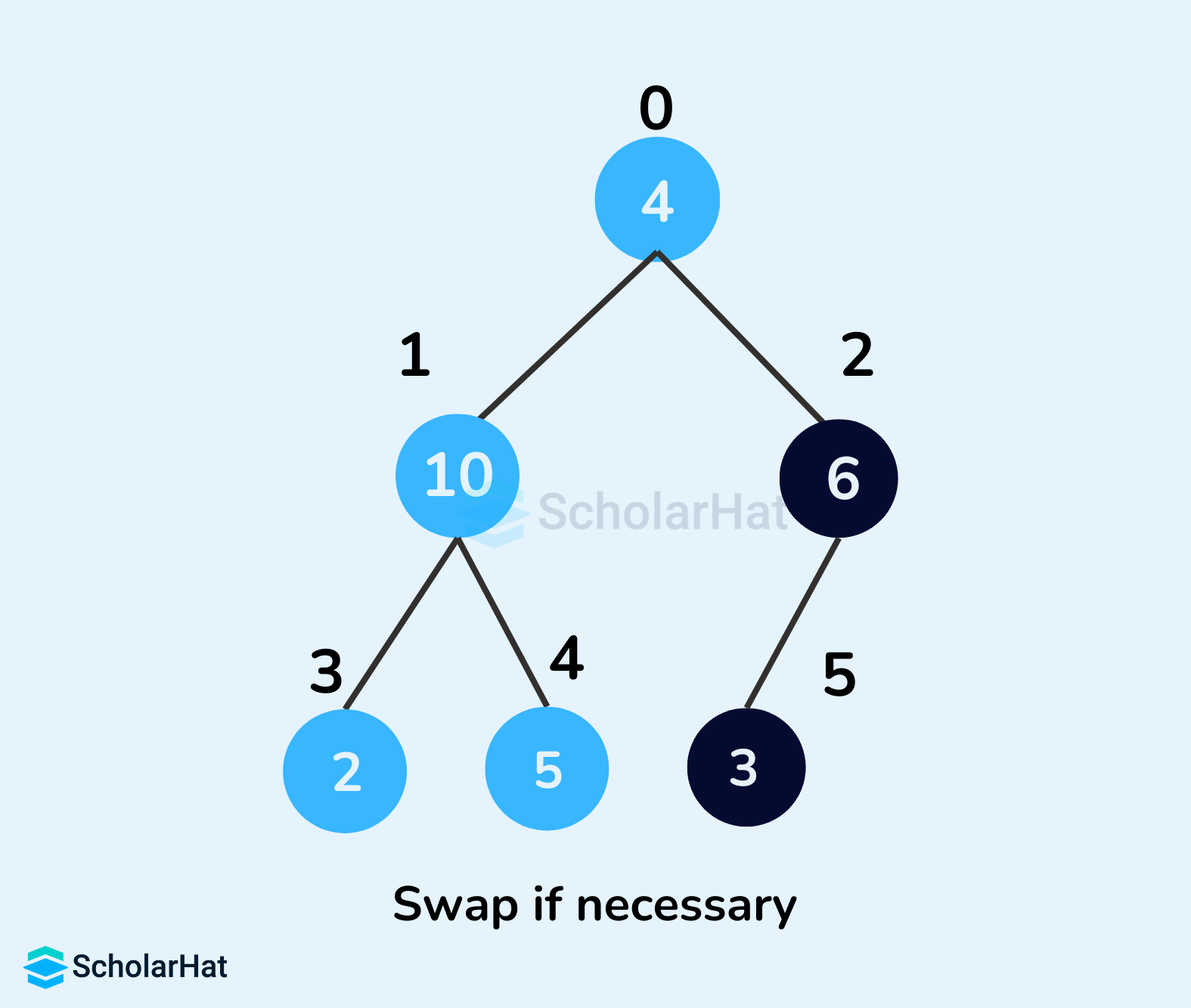
   • If leftChild is greater than currentElement (i.e. element at ith index), set leftChildIndex as largest.
   • If rightChild is greater than the element in largest, set rightChildIndex as largest.
6. Swap largest with currentElement



7. Repeat steps 3-7 until the subtrees are also heapified.

Algorithm to create a Max-Heap

MaxHeap(array, size)
  loop from the first index of non-leaf node down to zero
    call heapify

For Min-Heap, both leftChild and rightChild must be larger than the parent for all nodes.

2. Insertion

To insert a new element into a heap, it is added as a new leaf node and then "bubbled up" to its correct position to maintain the heap property.

For a min-heap, the new element is compared with its parent node and swapped if it is smaller. The swapping is repeated until the new element is in its correct position. The same process is followed for a max-heap, but the new element is compared with its parent node and swapped if it is larger.

Algorithm for Insertion in a Max Heap

If there is no node, 
  create a newNode.
else (a node is already present)
  insert the newNode at the end (last node from left to right.)
  
heapify the array

For Min Heap, the above algorithm is modified so that parentNode is always smaller than newNode.

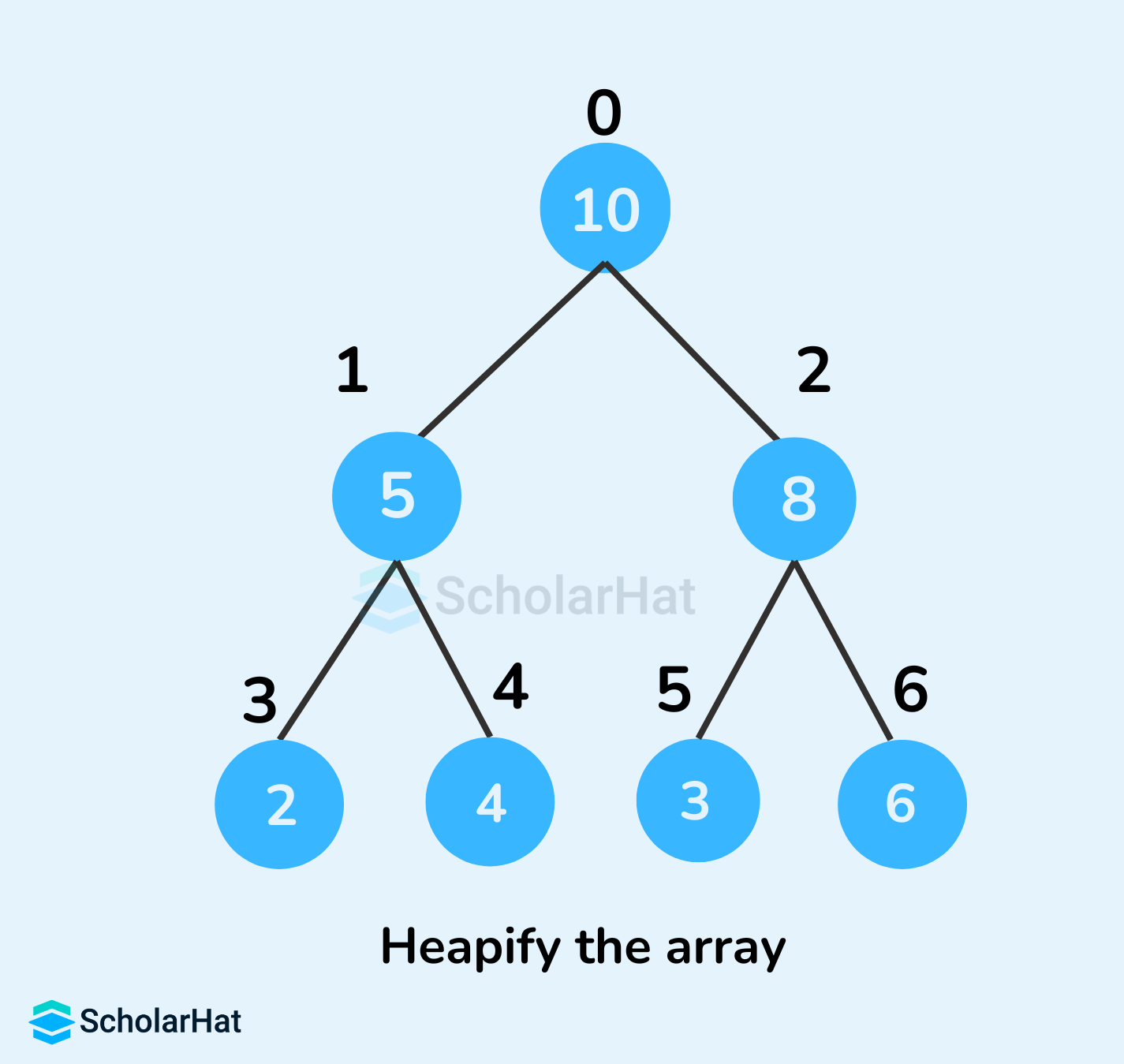
Example to illustrate Insertion in a Max Heap

1. Insert the new element at the end of the tree.

   

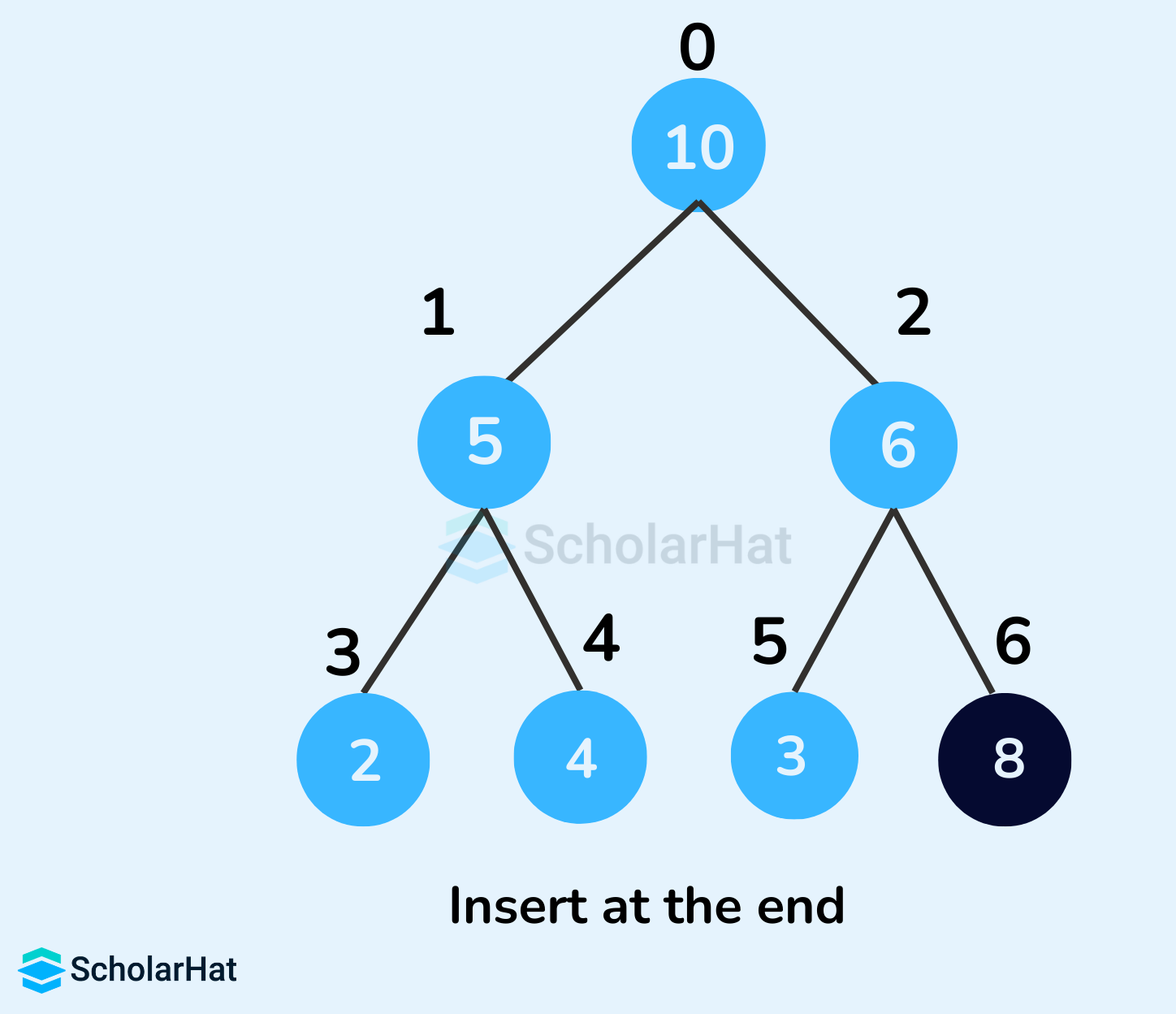
2. Heapify the tree.

   

3. Deletion

To remove an element from a heap, the root node (which always has the minimum or maximum value) is removed and replaced with the last leaf node. The new root is then bubbled down to its correct position to maintain the heap property.

For a min-heap, the new root is compared with its children and swapped with the smallest child if it is larger. The swapping is repeated until the new root is in its correct position. The same process is followed for a max-heap, but the new root is compared with its children and swapped with the largest child if it is smaller.

Algorithm for Deletion in a Max Heap

If nodeToBeDeleted is the leafNode
  remove the node
Else swap nodeToBeDeleted with the lastLeafNode
  remove noteToBeDeleted
   
heapify the array

For Min Heap, the above algorithm is modified so that both childNodes are greater or smaller than currentNode.

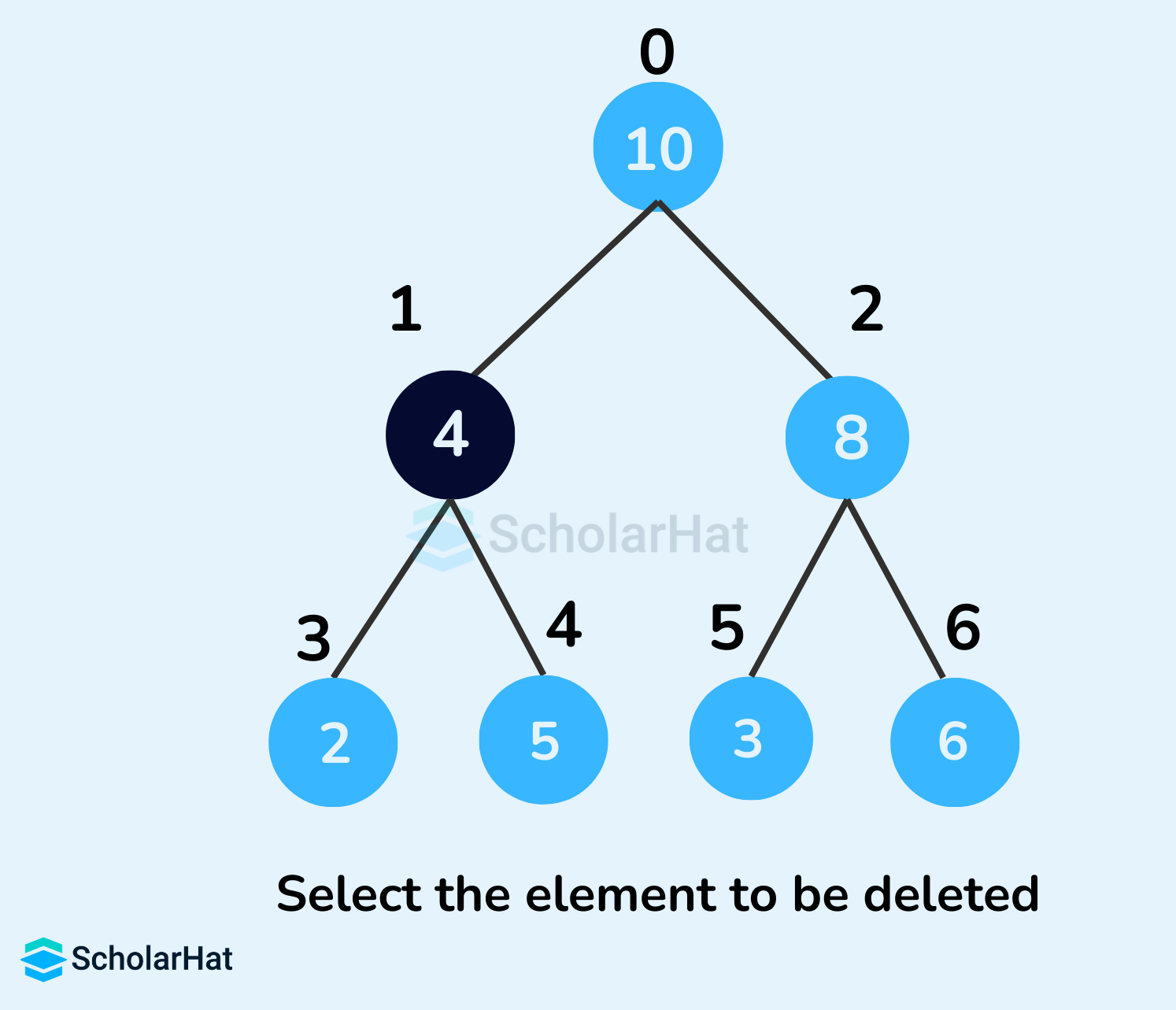
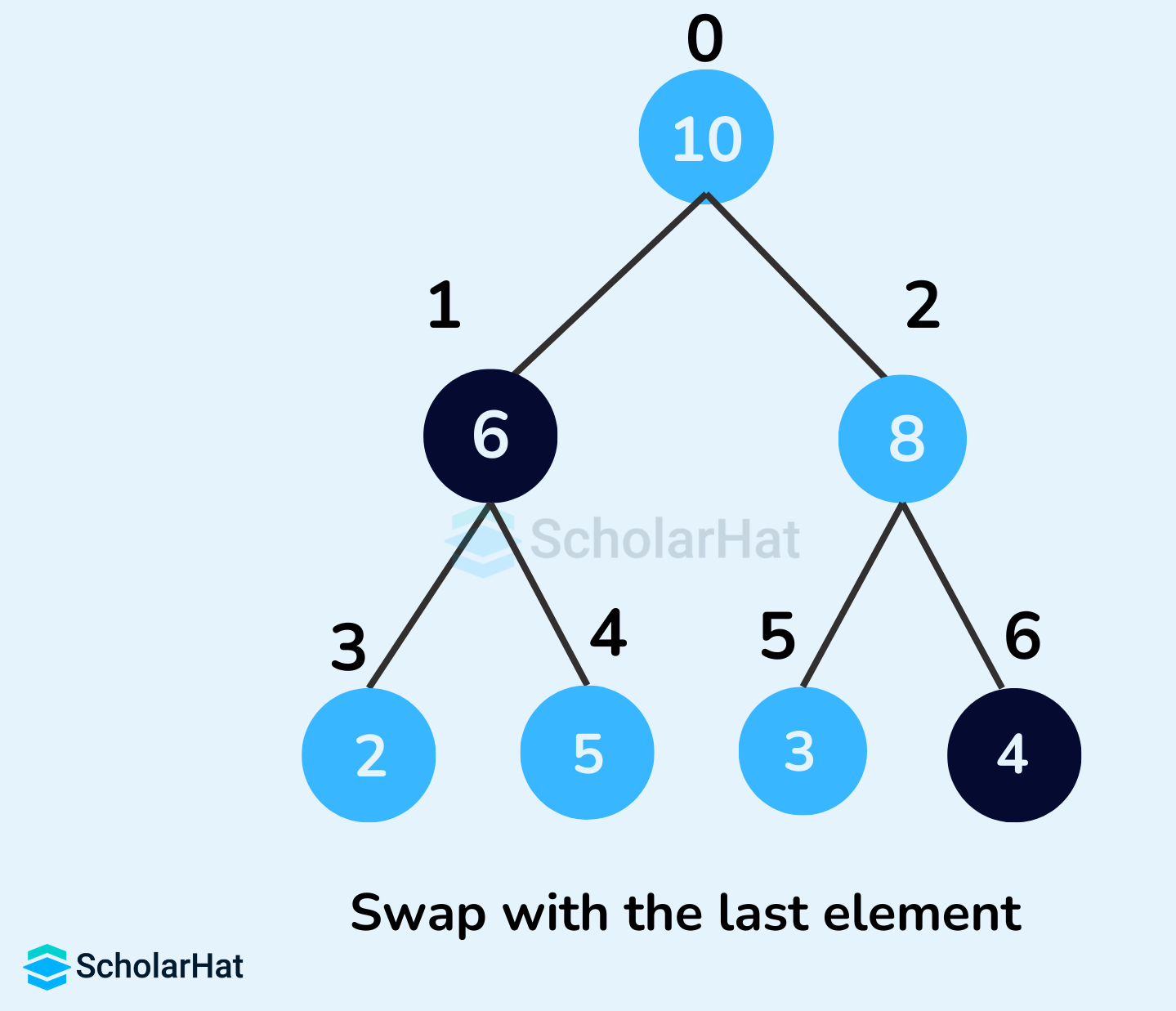
Example to illustrate Deletion in a Max Heap

1. Select the element to be deleted.

   

2. Swap it with the last element.

   

3. Remove the last element.

   

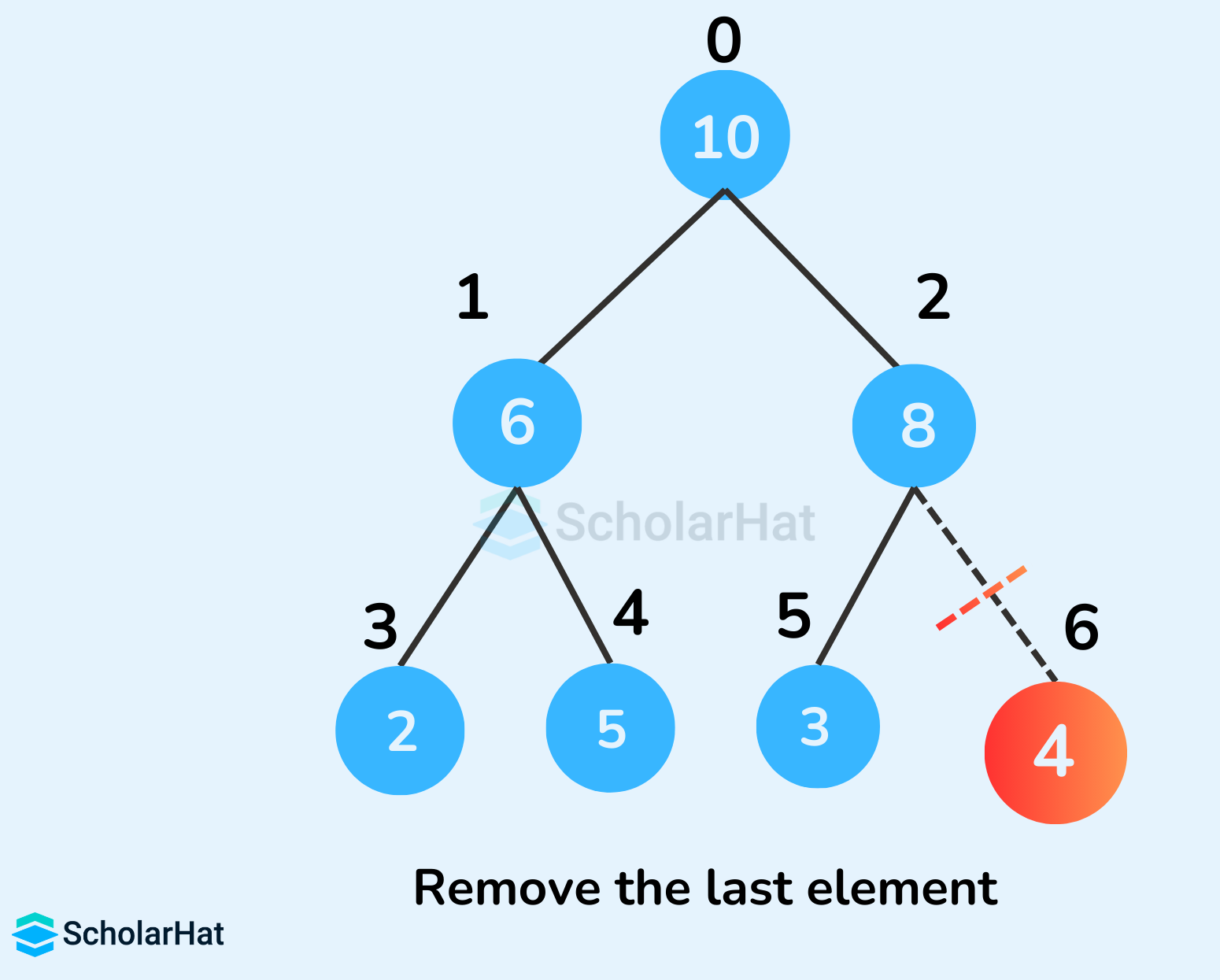
4. Heapify the tree.

   

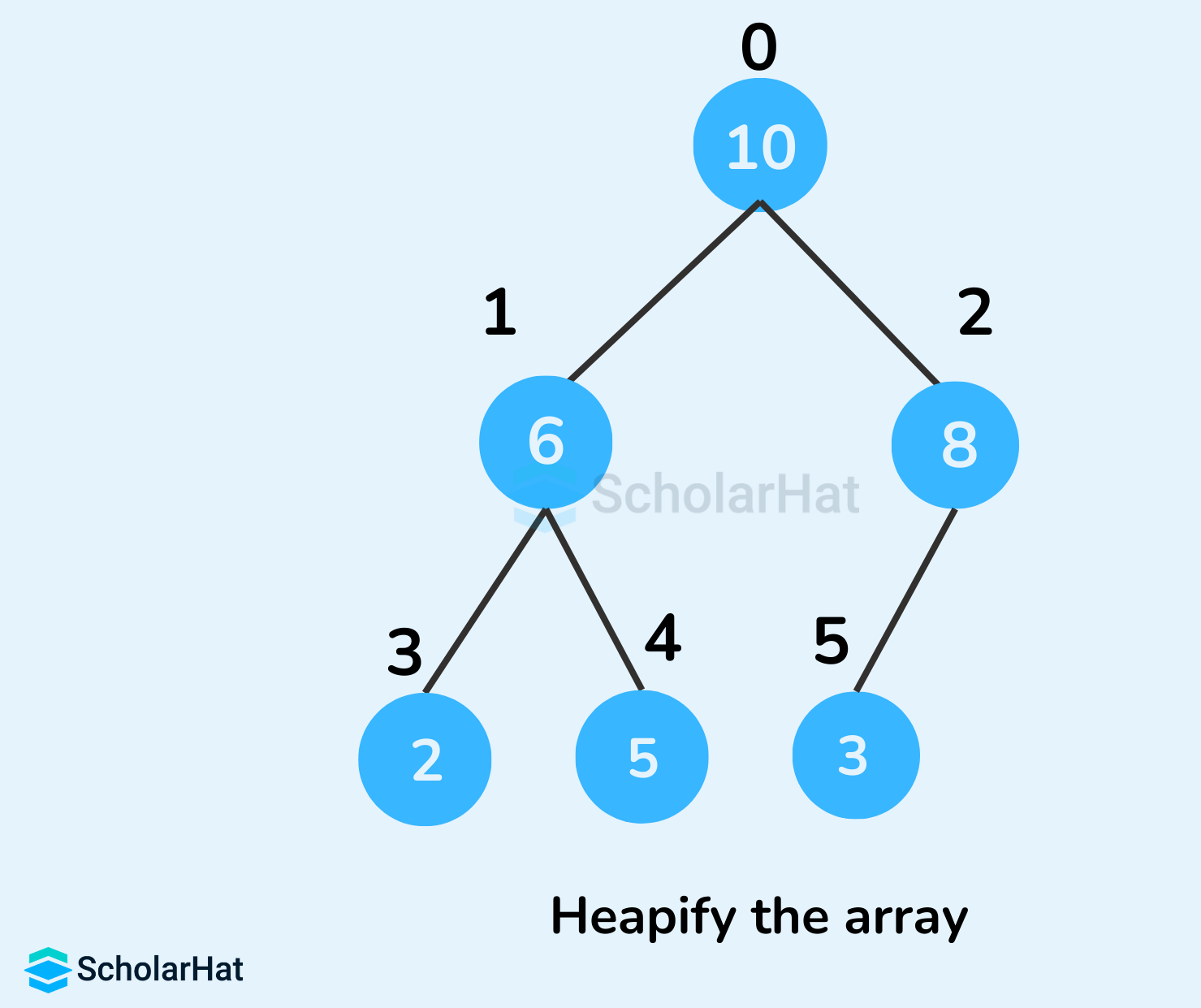
4. Peek(Find max/min)

Peek operation returns the maximum element from Max Heap or minimum element from Min Heap without deleting the node.

return rootNode

5. Extract-Max/Min

Extract-Max returns the node with maximum value after removing it from a Max Heap whereas Extract-Min returns the node with minimum after removing it from Min Heap.

Implementation of a Heap in Different Programming Languages

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2
    
    if l < n and arr[i] < arr[l]:
        largest = l
    
    if r < n and arr[largest] < arr[r]:
        largest = r
    
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def insert(array, newNum):
    size = len(array)
    if size == 0:
        array.append(newNum)
    else:
        array.append(newNum)
        for i in range((size//2)-1, -1, -1):
            heapify(array, size, i)

def deleteNode(array, num):
    size = len(array)
    i = 0
    for i in range(0, size):
        if num == array[i]:
            break
        
    array[i], array[size-1] = array[size-1], array[i]

    array.remove(num)
    
    for i in range((len(array)//2)-1, -1, -1):
        heapify(array, len(array), i)
        
def print_list(arr):
    for i in range(len(arr)):
        print(arr[i], end=" ")
    print()
    
arr = []

insert(arr, 7)
insert(arr, 5)
insert(arr, 8)
insert(arr, 4)
insert(arr, 2)

print("Max-Heap array: ", end=" ")
print_list(arr)

deleteNode(arr, 4)

print("After deleting an element: ", end=" " )
print_list(arr)
    

import java.util.ArrayList;

class Heap {
  void heapify(ArrayList hT, int i) {
    int size = hT.size();
    int largest = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    if (l < size && hT.get(l) > hT.get(largest))
      largest = l;
    if (r < size && hT.get(r) > hT.get(largest))
      largest = r;

    if (largest != i) {
      int temp = hT.get(largest);
      hT.set(largest, hT.get(i));
      hT.set(i, temp);

      heapify(hT, largest);
    }
  }

  void insert(ArrayList hT, int newNum) {
    int size = hT.size();
    if (size == 0) {
      hT.add(newNum);
    } else {
      hT.add(newNum);
      for (int i = size / 2 - 1; i >= 0; i--) {
        heapify(hT, i);
      }
    }
  }

  void deleteNode(ArrayList hT, int num)
  {
    int size = hT.size();
    int i;
    for (i = 0; i < size; i++)
    {
      if (num == hT.get(i))
        break;
    }

    int temp = hT.get(i);
    hT.set(i, hT.get(size-1));
    hT.set(size-1, temp);

    hT.remove(size-1);
    for (int j = size / 2 - 1; j >= 0; j--)
    {
      heapify(hT, j);
    }
  }

  void printArray(ArrayList array, int size) {
    for (Integer i : array) {
      System.out.print(i + " ");
    }
    System.out.println();
  }

  public static void main(String args[]) {

    ArrayList array = new ArrayList();
    int size = array.size();

    Heap h = new Heap();
    h.insert(array, 7);
    h.insert(array, 5);
    h.insert(array, 8);
    h.insert(array, 4);
    h.insert(array, 2);

    System.out.print("Max-Heap array: ");
    h.printArray(array, size);

    h.deleteNode(array, 4);
    System.out.print("After deleting an element: ");
    h.printArray(array, size);
  }
}
    

#include <iostream>
#include <vector>
using namespace std;

void swap(int *a, int *b)
{
  int temp = *b;
  *b = *a;
  *a = temp;
}
void heapify(vector &hT, int i)
{
  int size = hT.size();
  int largest = i;
  int l = 2 * i + 1;
  int r = 2 * i + 2;
  if (l < size && hT[l] > hT[largest])
    largest = l;
  if (r < size && hT[r] > hT[largest])
    largest = r;

  if (largest != i)
  {
    swap(&hT[i], &hT[largest]);
    heapify(hT, largest);
  }
}
void insert(vector &hT, int newNum)
{
  int size = hT.size();
  if (size == 0)
  {
    hT.push_back(newNum);
  }
  else
  {
    hT.push_back(newNum);
    for (int i = size / 2 - 1; i >= 0; i--)
    {
      heapify(hT, i);
    }
  }
}
void deleteNode(vector &hT, int num)
{
  int size = hT.size();
  int i;
  for (i = 0; i < size; i++)
  {
    if (num == hT[i])
      break;
  }
  swap(&hT[i], &hT[size - 1]);

  hT.pop_back();
  for (int i = size / 2 - 1; i >= 0; i--)
  {
    heapify(hT, i);
  }
}
void printArray(vector &hT)
{
  for (int i = 0; i < hT.size(); ++i)
    cout << hT[i] << " ";
  cout << "\n";
}

int main()
{
  vector heapTree;

  insert(heapTree, 7);
  insert(heapTree, 5);
  insert(heapTree, 8);
  insert(heapTree, 4);
  insert(heapTree, 2);

  cout << "Max-Heap array: ";
  printArray(heapTree);

  deleteNode(heapTree, 4);

  cout << "After deleting an element: ";

  printArray(heapTree);
}
    

Output

Max-Heap array:  8 5 7 4 2 
After deleting an element:  8 5 7 2    

Applications of the Heap

1. Priority Queues: A priority queue is a collection of elements where each element has a priority associated with it. Elements with higher priority are dequeued before elements with lower priority. The heap data structure is well suited for this application because it allows for efficient insertion and removal of elements while maintaining the priority order.
2. Graph Algorithms: Heap data structure can be used to efficiently implement several graph algorithms, including Dijkstra's shortest path algorithm and Prim's minimum spanning tree algorithm. In these algorithms, the heap data structure is used to store the vertices or edges of the graph in a priority queue, with the priority being the distance or weight of the path.
3. Sorting: Heap sort is a sorting algorithm that uses the heap data structure to sort an array of elements. The basic idea of the algorithm is to first build a heap from the input array and then repeatedly remove the largest element from the heap and place it at the end of the sorted array.
4. Memory Management: The heap data structure is also used for memory management in programming languages like C and C++. In these languages, the heap is a region of memory where dynamically allocated memory is stored. The heap data structure is used to keep track of the free and allocated memory blocks in the heap.
5. Event-driven Simulation: The heap data structure is used in event-driven simulation, where events are stored in a priority queue based on their time of occurrence. The heap data structure allows for the efficient insertion and removal of events while maintaining the correct ordering.

Summary

Hence, we can say that a heap in data structures is certainly a powerful and useful tool for any programmer. In this article, we have explored the wide range of capabilities these structures can enable for applications, from sorting and organizing to preventing memory overflow errors. Learning about heaps has revealed that they are highly beneficial and can provide some unique advantages over other solutions. For the implementation of your theoretical knowledge consider our, Data Structures and Algorithms Certification course.