13
FebHeap Sort Algorithm in Data Structures - Its Working, Implementation & Applications
Heap Sort in Data Structures: An Overview
We have learned the selection sort algorithm in the previous tutorials. In this DSA tutorial, we will understand a similar sorting technique, heap sort which is based on the concept of binary heap. We will understand its principle, algorithm, working, implementation, etc.DSA proficiency is valued by 90% of software engineering recruiters. Kickstart your career with our Free DSA Course with Certificate now!
What is Heap Sort in Data Structures?
Heap sort is a comparison-based, in-place sorting algorithm that visualizes the elements of the array in the form of a heap data structure to sort it. It divides the input array into two parts; sorted region, and unsorted region. The sorted region is initially empty, while the unsorted region contains all the elements. The largest element from the unsorted region is picked iteratively and added to the sorted region. The algorithm arranges the unsorted region in a heap.Before starting with the heap sort algorithm, you must have an understanding of arrays, trees in data structures, binary tree, complete binary tree, and heap data structures.
We will even see here some of the important concepts from these topics to understand the heap sort algorithm thoroughly.
| Similar Sorting Algorithms > Bubble Sort > Merge Sort > Quick Sort > Selection Sort > Counting Sort |
Array Representation of Binary Trees
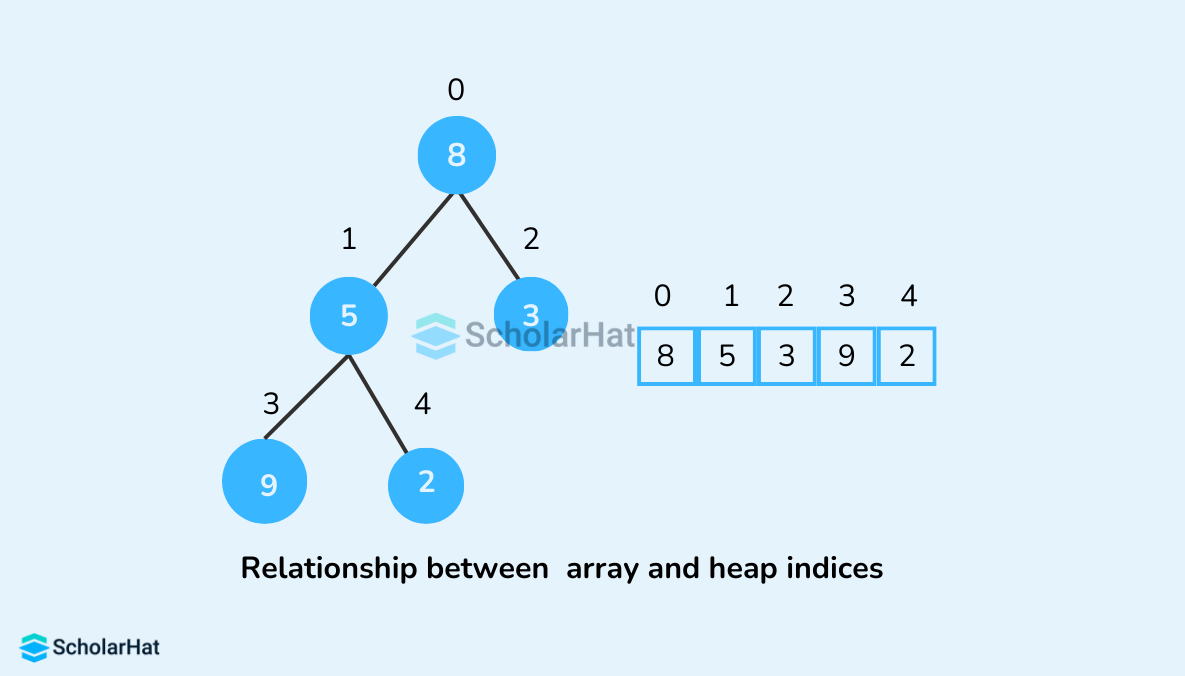
We can arrange the elements of a binary tree in an array. And, the indexes of the elements in this array can be used to find the parent or children of any node.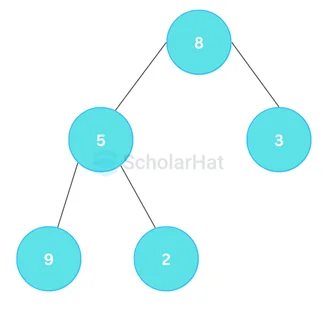 Consider the above-given tree. It has 5 nodes, and each node can be arranged as an element of an array in the following manner.
Consider the above-given tree. It has 5 nodes, and each node can be arranged as an element of an array in the following manner.
If the index of any given element in this array is i, then
- 2∗i+1: The element at this index becomes the left child of the element at i.
- 2∗i+2: The element at this index becomes the right child of the element at i.
- (i−1)/2: The element at the lower bound of this index gives the parent element of the ith element.
Let's suppose i=0, then
- Left child of element 8 = element at (2*0+1) index = element at 1st index = 5
- Right child of element 8 = element at (2*0+2) index = element at 2nd index = 3
Now let's suppose i=3, then
- Parent of element 9 = element at (3-1)/2 = element at 1st index = 5
Read More - Data Structure Interview Questions for Freshers
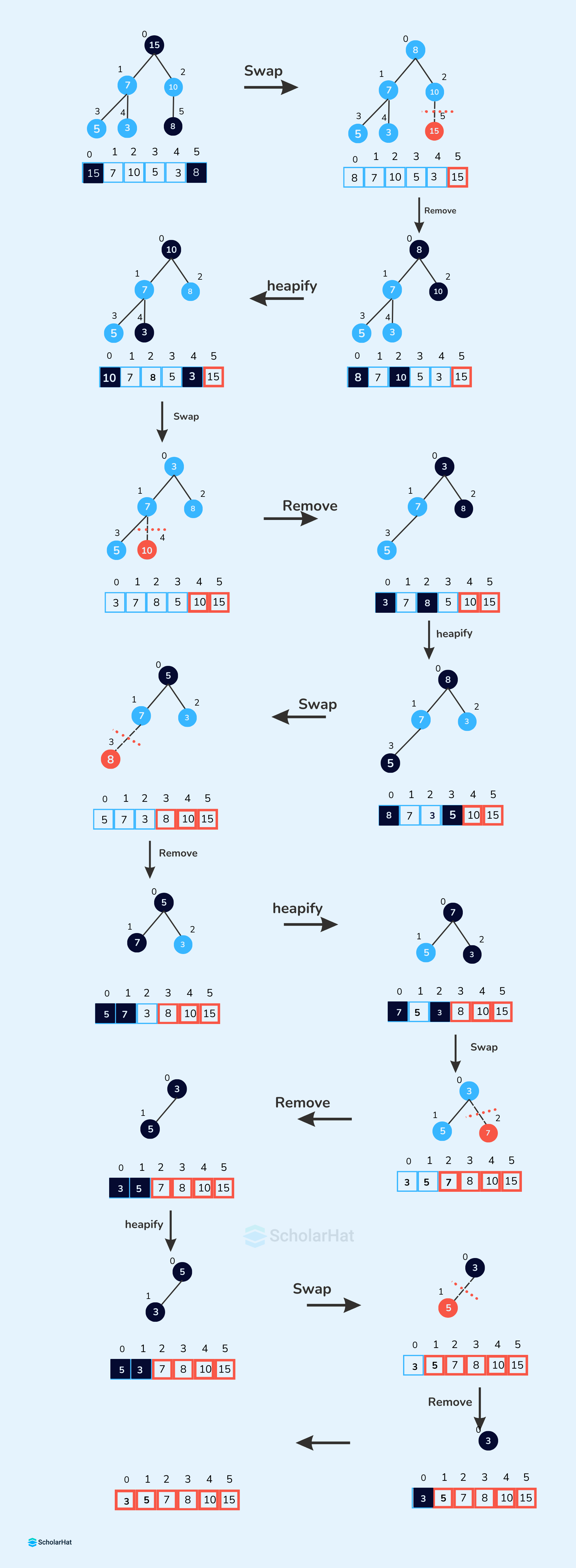
Working of Heap Sort Algorithm
- Build Max Heap: Create a max heap by visualizing all the elements of the array in a binary tree. This process ensures that the largest element is at the root of the heap.
- Repeat the following steps until the heap contains only one element:
- Swap: Remove the root element and put it at the end of the array (nth position). Put the last item of the tree (heap) in the vacant place.
- Remove: Reduce the size of the heap by 1.
- Heapify: Heapify the root element again so that we have the highest element at the root.
- Obtain Sorted Array: The sorted array is obtained by reversing the order of the elements in the input array.
We'll discuss each step in detail below
How to Heapify a Tree?
Heapify is the process of rearranging the elements to form a tree that maintains the properties of the heap data structure. After inserting the elements into a heap, they may or may not satisfy the heap properties. In that case, we need to rearrange the locations of the elements in the erroneous heap to make it a heap again. Starting from a complete binary tree, we can modify it to become a Max-Heap by running a function called heapify on all the non-leaf elements of the heap.Let's first heapify a tree with just three elements.
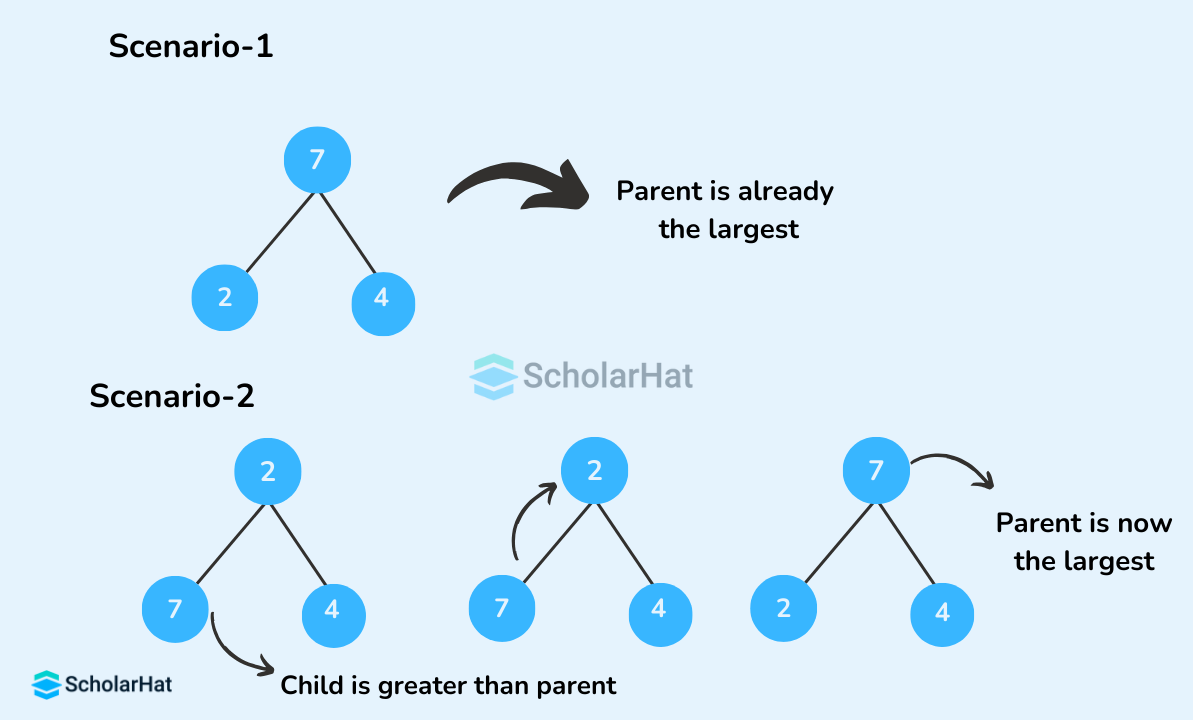
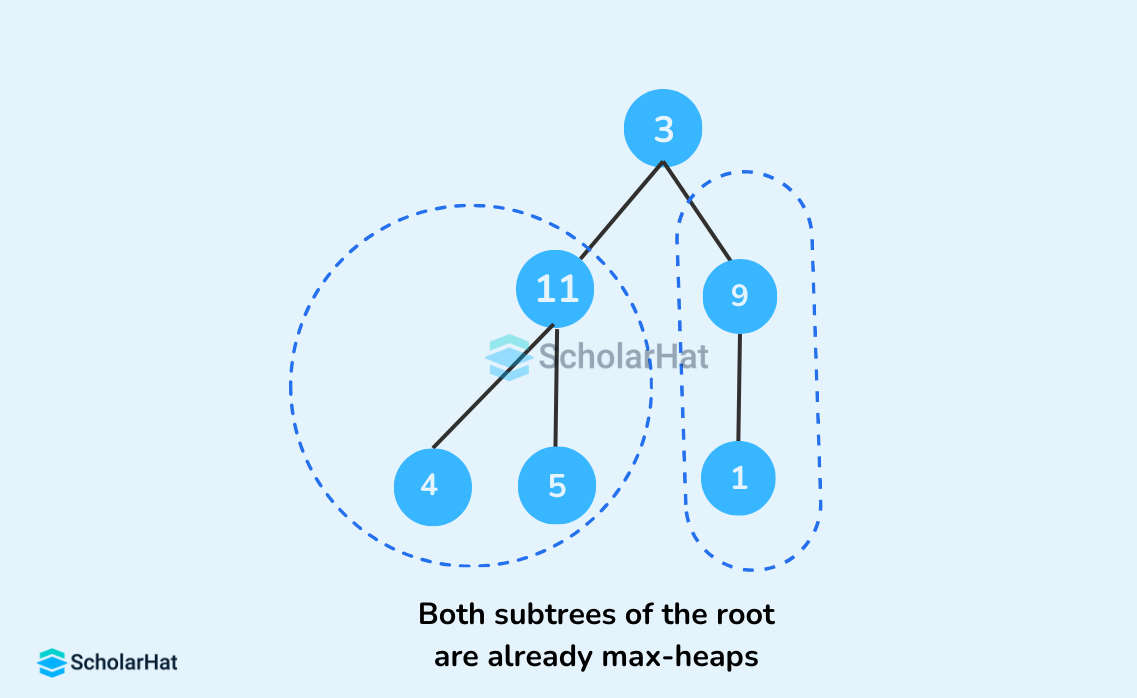
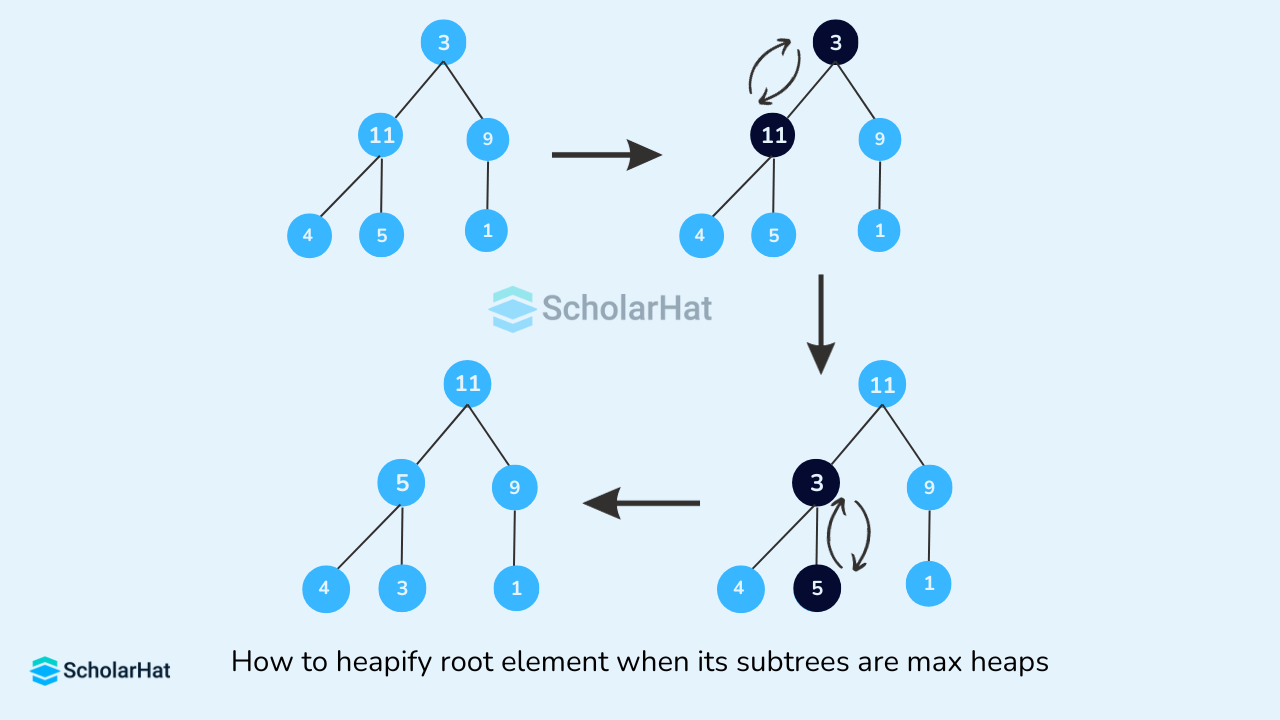
heapify() that is run on the root node (0th index) and can be called recursively until a max-heap is obtained.Algorithm for heapify()
heapify(array, n, index) {
size = array.size()
largest = index
left = 2 * index + 1
right = 2 * index + 2
if left < n && arr[left] > arr[largest]
largest = left
if right < n && arr[right] > arr[largest]
largest = right
if largest != index {
swap arr[index], arr[largest]
heapify(arr, n, largest)
}
}
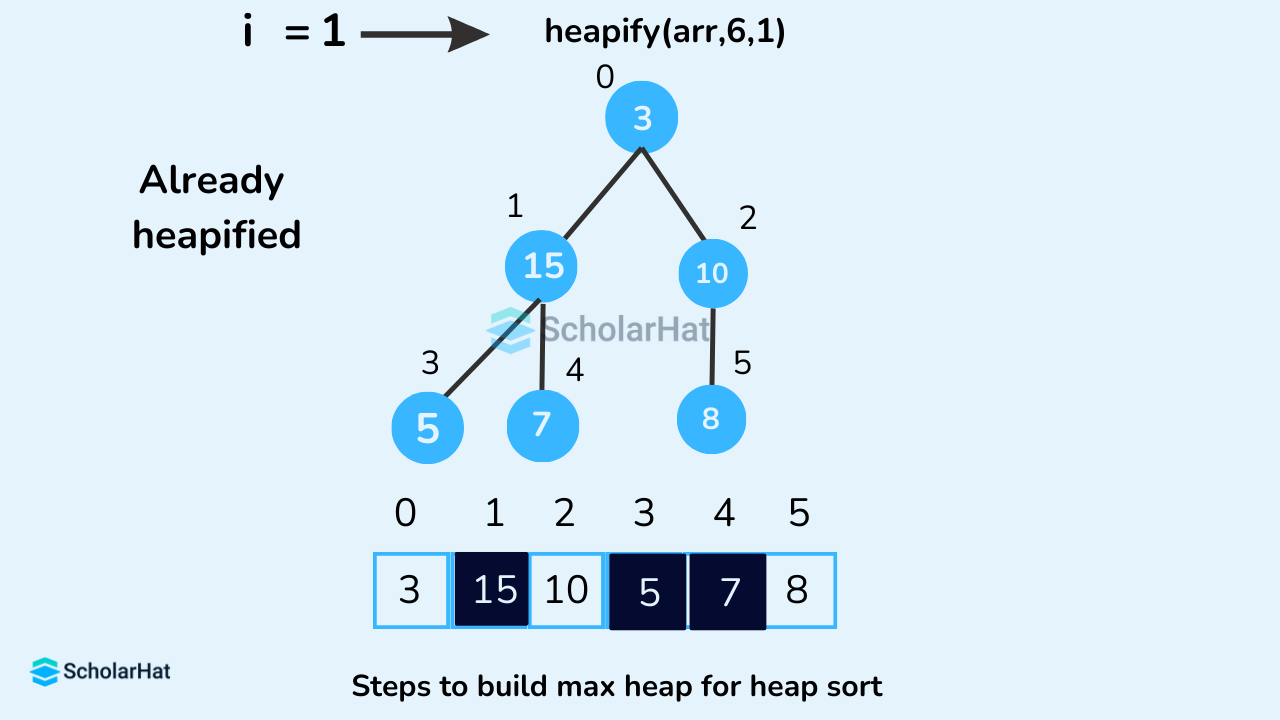
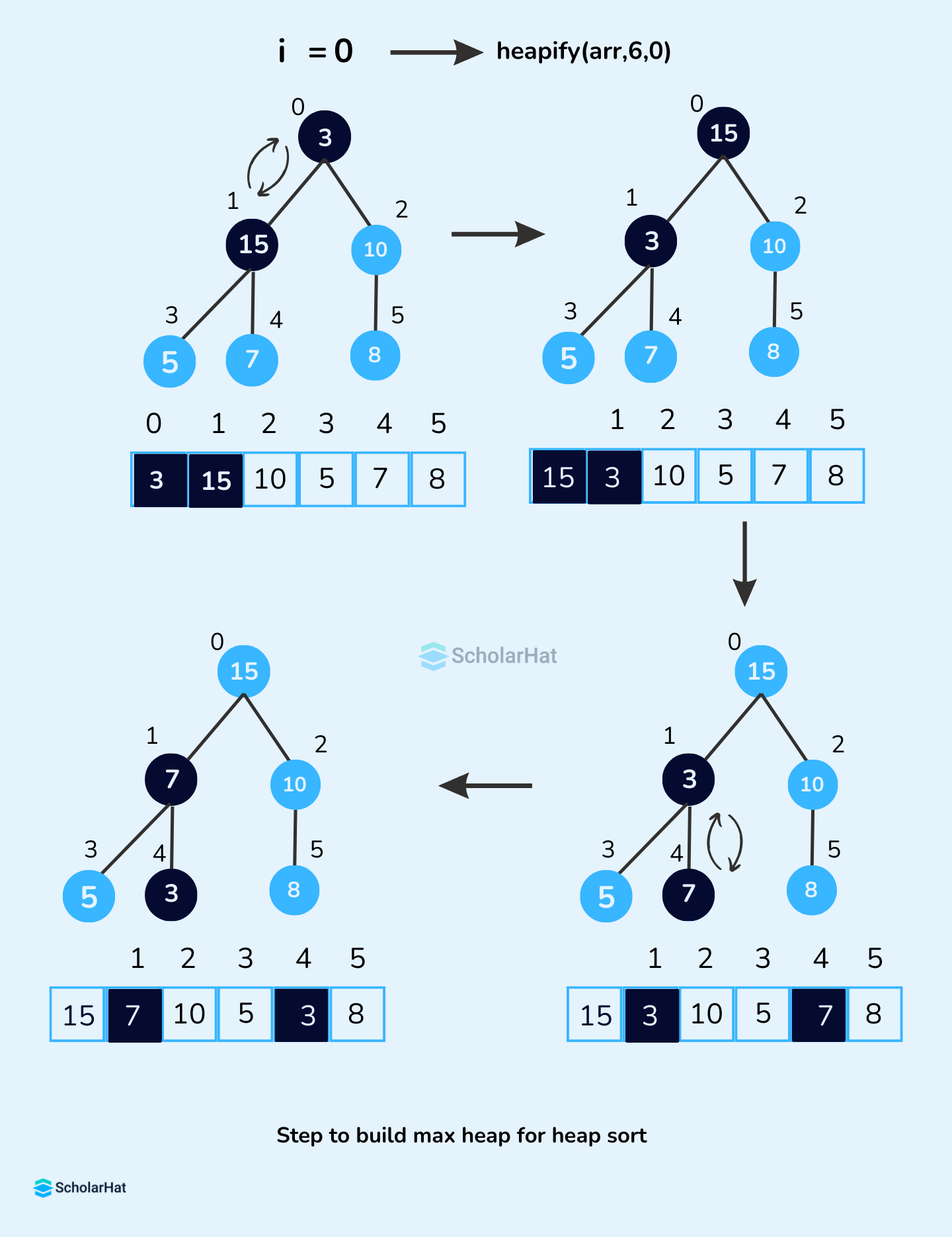
Build Max-Heap
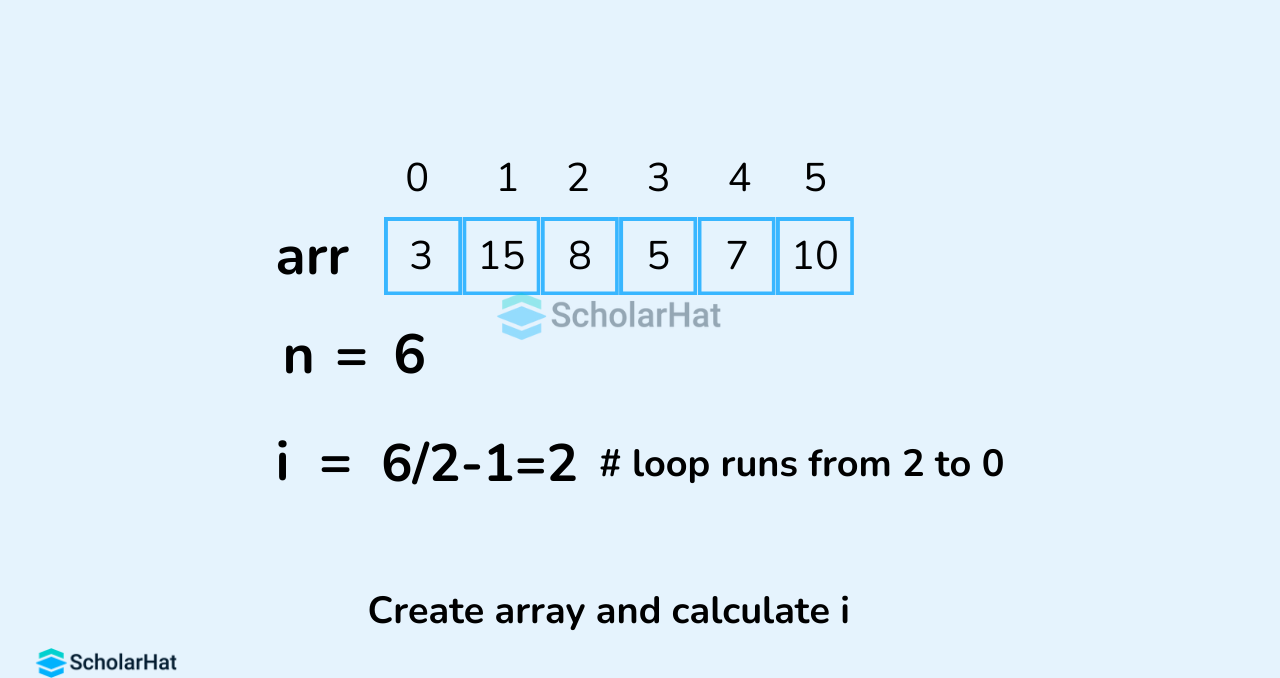
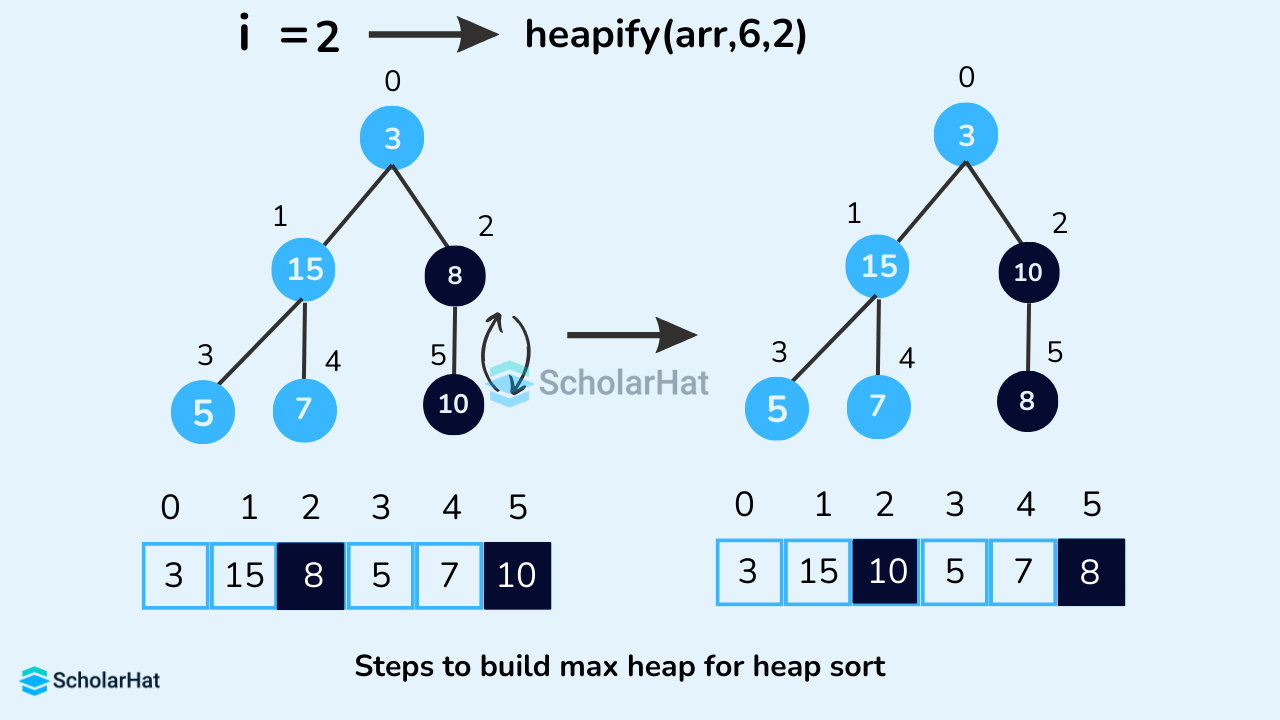
To build a max-heap from any tree, we can thus start heapifying each sub-tree from the bottom up and end up with a max-heap after the function is applied to all the elements including the root element. In the case of a complete tree, the first index of a non-leaf node is given by n/2 - 1. All other nodes after that are leaf nodes and thus don't need to be heapified. So, we can build a maximum heap as // Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
Swap, Remove, Heapify
Heap Sort Algorithm
for i = n - 1 till i >= 0:
// taking the largest number from and the heap and placing it at the end
swap arr[0], arr[i]
// Heapifying the tree recursively starting from index 0
heapify(arr, i, 0);
end for
Implementation of Heap Sort Algorithm in Different Programming Languages
def heapify(arr, n, i):
# Finding left and right child
largest = i
left = 2 * i + 1
right = 2 * i + 2
# Setting the largest out of root, left child & right child
if left < n and arr[i] < arr[left]:
largest = left
if right < n and arr[largest] < arr[right]:
largest = right
# If root is not the largest, swap
if largest != i:
# Swap root with the largest
arr[i], arr[largest] = arr[largest], arr[i]
# Calling the heapify function recursively
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
# Building a max-heap for each iteration of the loop
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n - 1, 0, -1):
# Swap the elements at i’th and 0th indexes
arr[i], arr[0] = arr[0], arr[i]
# Heapify the root element recursively
heapify(arr, i, 0)
def print_list(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
original_array = [3, 15, 8, 5, 7, 10]
sorted_array = original_array.copy()
print("Original array:", end=" ")
print_list(original_array)
heapSort(sorted_array)
print("Sorted array:", end=" ")
print_list(sorted_array)
class HeapSort {
// Heap sort function
public void heapSort(int arr[]) {
int n = arr.length;
// Build a max-heap for each iteration of the loop
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// Heap sort
for (int i = n - 1; i >= 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// Heapify root element recursively
heapify(arr, i, 0);
}
}
// Heapify function
void heapify(int arr[], int n, int index) {
// Finding the left and the right child
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
// Setting the largest out of root, left child & right child
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
// If index is not equal to largest
if (largest != index) {
// Perform swap
int temp = arr[index];
arr[index] = arr[largest];
arr[largest] = temp;
// Calling the heapify function recursively
heapify(arr, n, largest);
}
}
// Utility method to print an array in a single line
static void printArrayInLine(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
}
// Utility method to print an array in a new line
static void printArray(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Main method
public static void main(String[] args) {
// Array to be sorted
int[] arr = {3, 15, 8, 5, 7, 10};
// Create an instance of HeapSort
HeapSort heapSort = new HeapSort();
// Print the original array in a single line
System.out.print("Original array: ");
printArray(arr);
// Perform Heap Sort
heapSort.heapSort(arr);
// Print the sorted array in a new line
System.out.print("Sorted array: ");
printArray(arr);
}
}
#include <iostream>
using namespace std;
// Function to heapify the tree
void heapify(int arr[], int n, int i) {
// Finding left & right child
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Setting the largest out of root, left child & right child
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
// If index is not equal to largest
if (largest != i) {
// using std::swap() to swap
swap(arr[i], arr[largest]);
// heapifying the tree recursively
heapify(arr, n, largest);
}
}
// Main function to do heap sort
void heapSort(int arr[], int n) {
// Building max heap by heapifying the elements
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// Heap sort
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
// Heapify root element recursively to get the highest element at root
heapify(arr, i, 0);
}
}
int main() {
int arr[] = {3, 15, 8, 5, 7, 10};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array: ";
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
// Perform heap sort
heapSort(arr, n);
cout << "\nSorted array: ";
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
return 0;
}
Output
Original array: 3 15 8 5 7 10
Sorted array: 3 5 7 8 10 15
Complexity Analysis of Heap Sort Algorithm
- Time Complexity
Case Time Complexity Best O(nlog n) Worst O(nlog n) Average O(nlog n) - Space Complexity: The space complexity is
O(1)because we have a fixed number of variables, and we do not need any extra memory space apart from the loop variables and auxiliary variables that include temp, n, index, and largest.
Applications of Heap Sort Algorithm
- Sorting: Heap sort can efficiently sort an array of elements in ascending or descending order. It has a worst-case time complexity of O(n log n), which makes it suitable for sorting large data sets.
- Priority Queue: Heap sort can be used to implement a priority queue, where each element has a priority associated with it. The heap structure allows for the efficient insertion and extraction of elements based on their priority.
- Selection of Top-K Elements: Heap sort can be used to efficiently find the top-k elements from a large dataset. By building a max-heap, the k largest elements can be extracted in O(k log n) time complexity.
- Median Finding: Heap sort can be employed to find the median of a dataset. By using two heaps (a max-heap for the lower half of elements and a min-heap for the upper half), the median can be determined in O(log n) time complexity for each element.
- External Sorting: Heap sort can be used in external sorting algorithms, where data is too large to fit entirely in memory. It can be applied in the initial phase of sorting, where chunks of data are sorted and written back to the disk before merging them.
Advantages of Heap Sort Algorithm
- Efficiency: Heap sort has a time complexity of O(n log n) in all cases, where 'n' is the number of elements to be sorted. This makes it more efficient than many other sorting algorithms, such as bubble sort or insertion sort, which have higher time complexities in the worst case.
- Space efficiency: Heap sort sorts the elements in place, meaning it does not require additional memory proportional to the number of elements being sorted. It achieves this by utilizing the original array to build a binary heap and then performing in-place swaps to sort the elements.
- Guaranteed worst-case performance: Unlike some other sorting algorithms, such as quicksort, which have a worst-case time complexity of O(n^2) in certain scenarios, heap sort guarantees a worst-case time complexity of O(n log n) regardless of the input data distribution. This predictability makes it a reliable choice in situations where worst-case performance is critical.
- In-place sorting: As mentioned earlier, heap sort performs sorting in place, which means it does not require additional memory beyond the input array. This makes it suitable for situations where memory usage is a concern or when working with large datasets that may not fit into available memory.
- Stability: It preserves the relative order of elements with equal keys. This property can be important in certain applications where maintaining the original order of elements is necessary.
- Simplicity: The basic concept of the heap sort is relatively simple to understand compared to some other advanced sorting algorithms. It involves building a binary heap and repeatedly extracting the maximum (or minimum) element from the heap to construct the sorted array.
- Partial sorting: Heap sort can be easily modified to perform partial sorting, where only the top k elements are sorted, rather than the entire array. This feature can be useful in situations where only a subset of the largest or smallest elements is required
Disadvantages of Heap Sort Algorithm
- Not a stable sorting algorithm: Heap sort does not guarantee the relative order of elements with equal keys. If there are duplicate elements in the input array, their order may change after sorting. This makes heap sort unsuitable for sorting certain types of data where stability is important.
- Requires additional space: Heap sort requires additional space to build the heap data structure. The sorting algorithm itself is an in-place algorithm, meaning it sorts the elements within the input array without requiring additional memory. However, creating the heap initially requires a separate heap data structure, which can consume extra memory. This extra space requirement can be a disadvantage when working with large data sets.
- Poor cache performance: This is because heap sort accesses memory in a non-sequential manner, jumping between different parts of the heap. This irregular memory access pattern can lead to cache misses and slower performance, particularly when sorting large arrays.
- The complexity of implementation: Building the heap and performing the heapify operation to maintain the heap property requires careful implementation. This complexity can make heap sorting harder to understand and debug, especially for novice programmers.
- Not adaptive: Heap sort does not take advantage of any existing order in the input array. It always performs the same number of comparisons and swaps regardless of the initial order of the elements. This lack of adaptivity makes it less efficient than some other sorting algorithms when applied to partially sorted or nearly sorted arrays.
Summary
The Heap Sort algorithm is a powerful tool for sorting data efficiently and accurately. Its main advantages include its efficiency, in-place sorting capability, stability of the data after it has been sorted, fast performance in comparison to other sorting algorithms, and ease of implementation. For a more practical understanding, consider enrolling in our Free Dsa Course With Certificate.Java full stack developers get promoted 20% faster to senior roles. Accelerate your career with our Java full stack development course today!
Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.