Insertion Sort in Data Structures - Algorithm, Working, & Advantages

Insertion Sort: An Overview

Have you played cards? Many of you would have played. In this DSA tutorial, we are going to learn Insertion Sort which works exactly the way you sort the cards in your hands. To further enhance your understanding and application of insertion sort concepts, consider enrolling in the best Dsa Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Insertion Sort in Data Structures?

Insertion sort is a sorting algorithm in which the unsorted elements are transferred one at a time to the right position. Here, the array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed in the correct position in the sorted part. It is one of the simplest sorting techniques that we use in our daily lives.

Insertion Sort Algorithm

insertionSort(array)
 mark first element as sorted
 for each unsorted element X
  'extract' the element X
  for j <- lastSortedIndex down to 0
   if current element j > X
    move sorted element to the right by 1
  break loop and insert X here
end insertionSort

According to the algorithm, to sort an array of size n in ascending order iterate over the array, and compare the current element X to its predecessor, if X is smaller than its predecessor, compare it to the elements before. Move the greater elements one position up to make space for the swapped element.

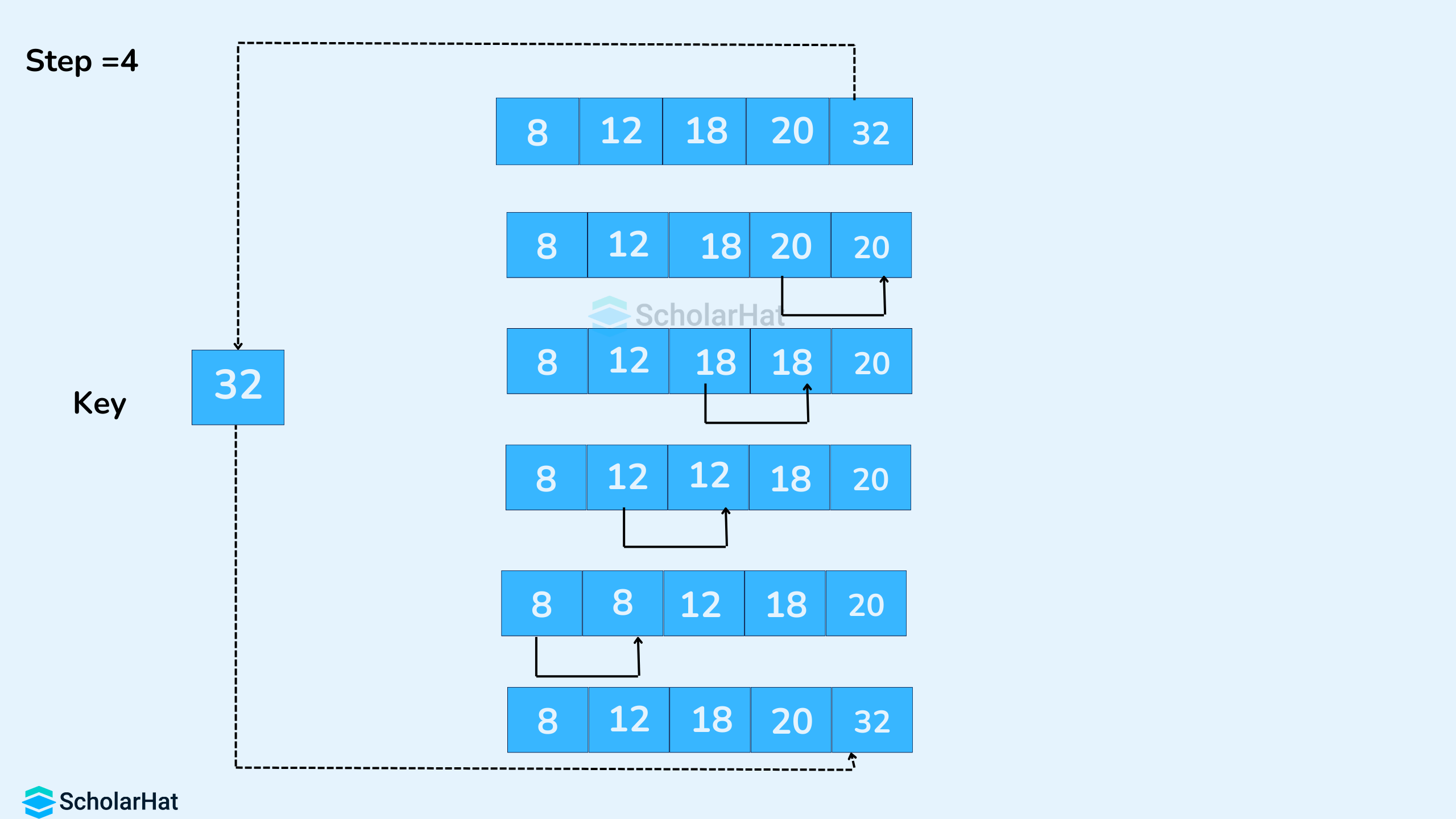
Working of Insertion Sort Algorithm

1. The first element in the array is assumed to be sorted. Take the second element and store it as key. Compare the key with the first element. If the first element is greater than the key, the key is placed in front of the first element.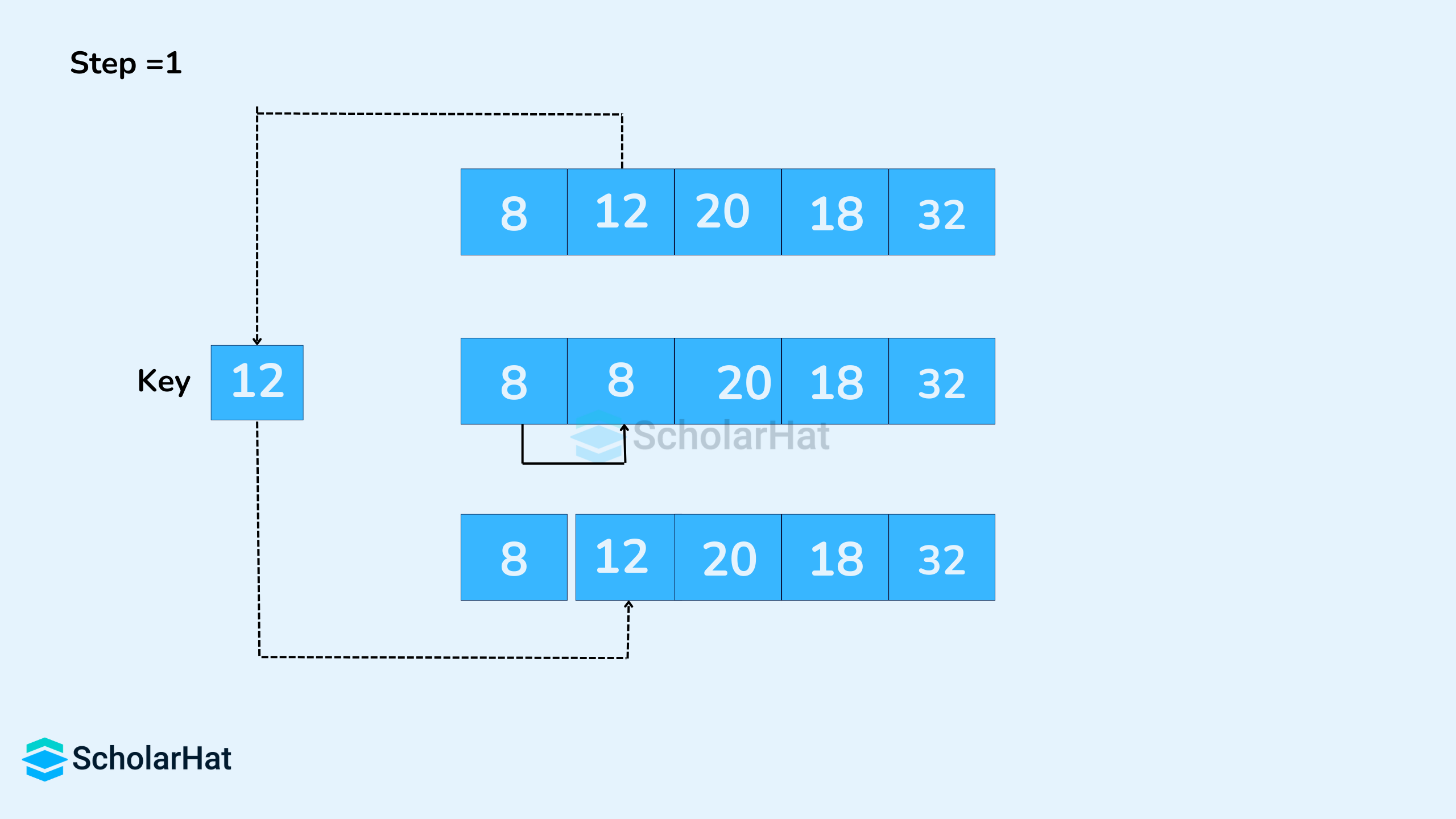

   

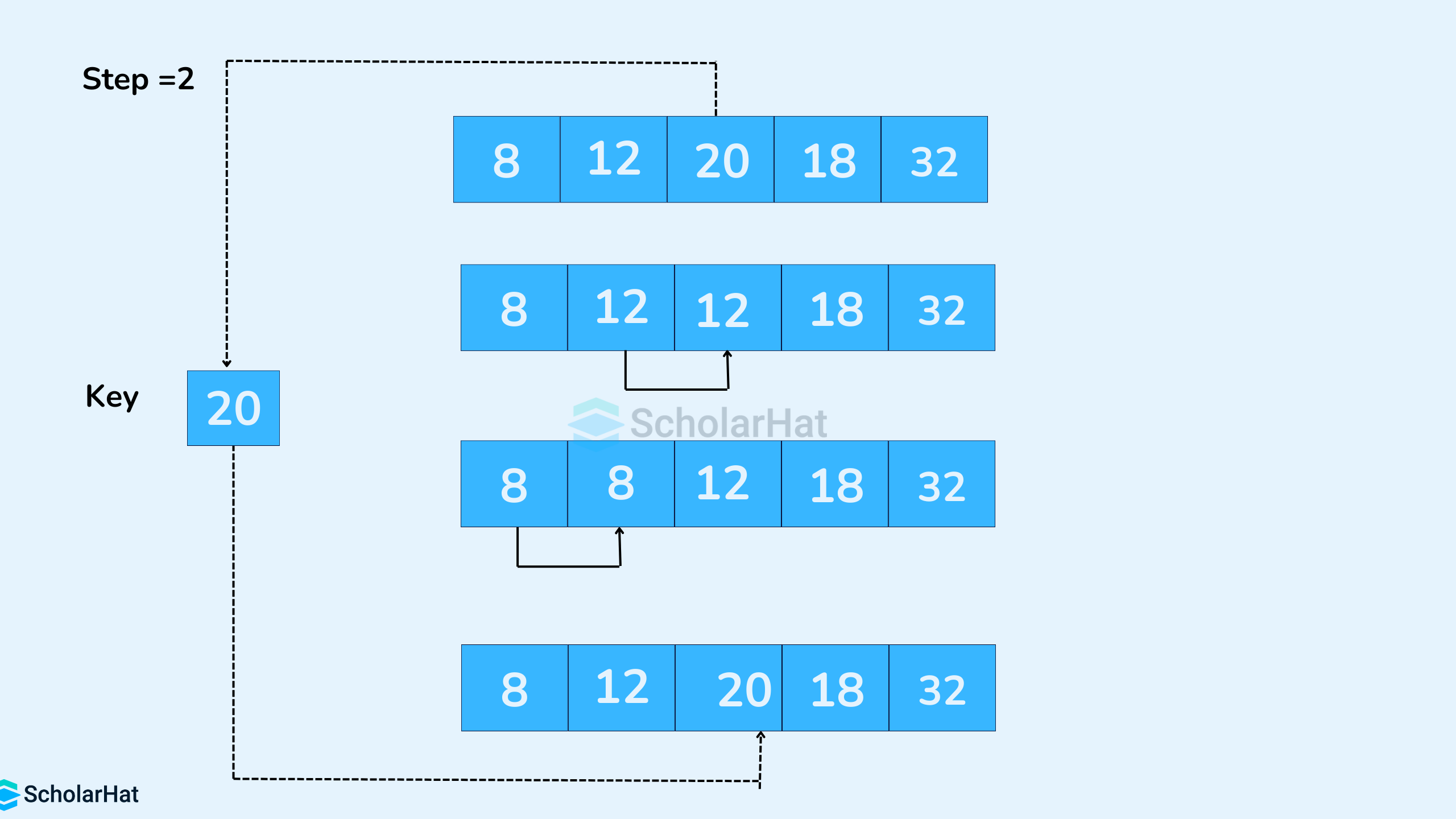
2. Now, the first two elements are sorted. Take the third element and compare it with the elements on the left of it. Plac it just behind the element smaller than it. If there is no element smaller than it, place it at the beginning of the array.

   

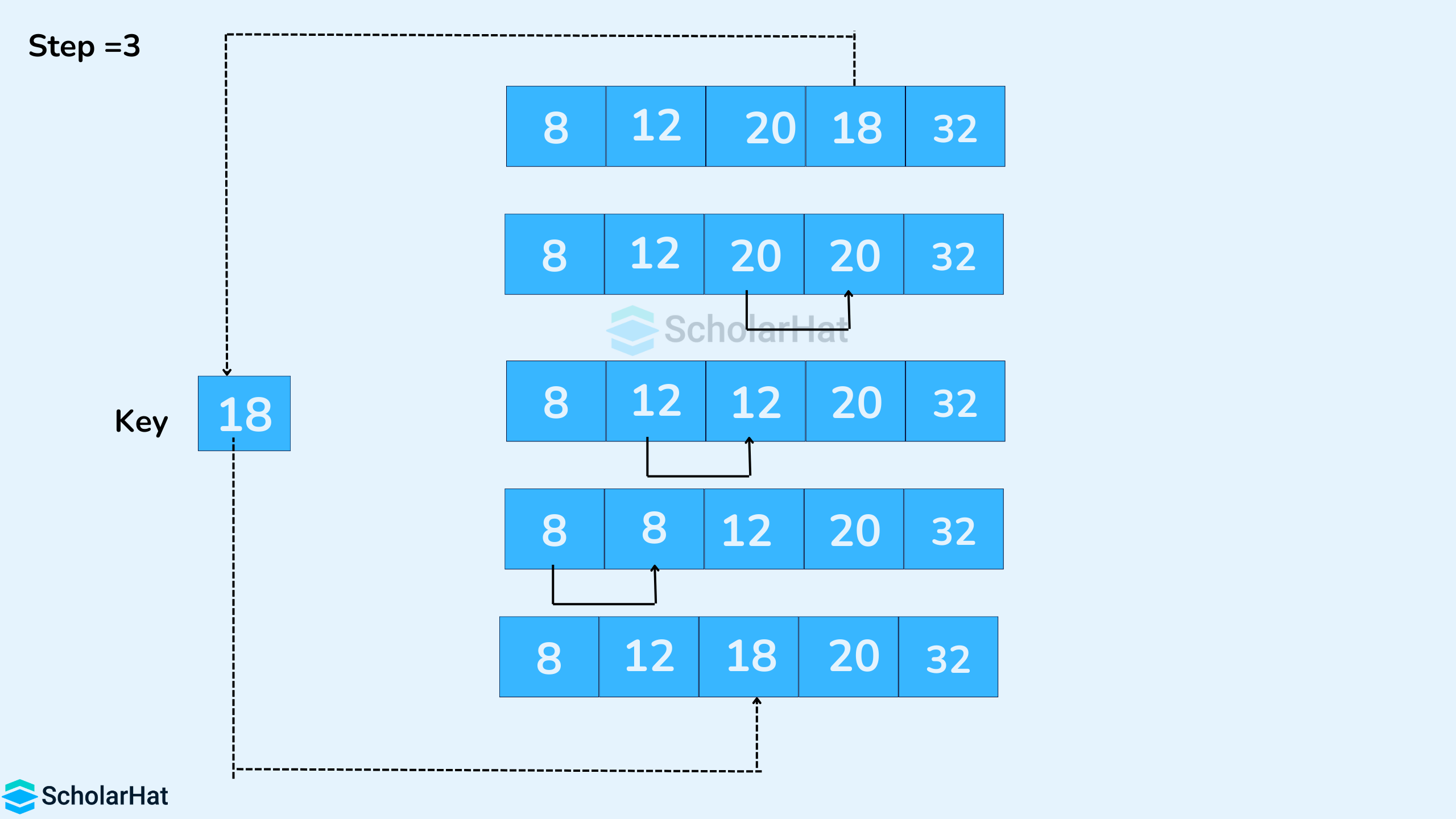
3. Similarly, place every unsorted element in its correct position.

   

   

Read More - Best Data Structure Interview Questions and Answers

Implementation of Insertion Sort in Different Languages in Data Structures

def insertionSort(array):
    for step in range(1, len(array)):
        key = array[step]
        j = step - 1

        # Compare key with each element on the left of it until an element smaller than it is found
        # For descending order, change key < array[j] to key > array[j].
        while j >= 0 and key < array[j]:
            array[j + 1] = array[j]
            j = j - 1

        # Place key after the element just smaller than it.
        array[j + 1] = key
        
def print_list(arr):
    for i in range(len(arr)):
        print(arr[i], end=" ")
    print()

arr = [8,12,20,18,32]
original_arr = arr.copy()

# Print the original array
print('Original Array:', end=" ")
print_list(arr)

insertionSort(arr)

# Print the sorted array in ascending order
print('Sorted Array in Ascending Order:', end=" ")
print_list(arr)
    

public class InsertionSort {
    static void insertionSort(int[] array) {
        for (int step = 1; step < array.length; step++) {
            int key = array[step];
            int j = step - 1;

            // Compare key with each element on the left of it until an element smaller than it is found
            // For descending order, change key < array[j] to key > array[j].
            while (j >= 0 && key < array[j]) {
                array[j + 1] = array[j];
                j = j - 1;
            }

            // Place key after the element just smaller than it.
            array[j + 1] = key;
        }
    }

    static void printArray(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] arr = {8, 12, 20, 18, 32};
        int[] originalArr = arr.clone();

        // Print the original array
        System.out.print("Original Array: ");
        printArray(originalArr);

        insertionSort(arr);

        // Print the sorted array in ascending order
        System.out.print("Sorted Array in Ascending Order: ");
        printArray(arr);
    }
}
    

#include <iostream>
using namespace std;

void insertionSort(int array[], int size) {
    for (int step = 1; step < size; step++) {
        int key = array[step];
        int j = step - 1;

        // Compare key with each element on the left of it until an element smaller than it is found
        // For descending order, change key < array[j] to key > array[j].
        while (j >= 0 && key < array[j]) {
            array[j + 1] = array[j];
            j = j - 1;
        }

        // Place key after the element just smaller than it.
        array[j + 1] = key;
    }
}

void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
}

int main() {
    int arr[] = {8, 12, 20, 18, 32};
    int size = sizeof(arr) / sizeof(arr[0]);
    int originalArr[size];

    // Copy the original array
    copy(arr, arr + size, originalArr);

    // Print the original array
    cout << "Original Array: ";
    printArray(originalArr, size);

    insertionSort(arr, size);

    // Print the sorted array in ascending order
    cout << "Sorted Array in Ascending Order: ";
    printArray(arr, size);

    return 0;
}
    

Output

Original Array: 8 12 20 18 32 
Sorted Array in Ascending Order: 8 12 18 20 32 

Complexity Analysis of Insertion Sort Algorithm

1. Time Complexity

   Case	Time Complexity
   Best	O(n)
   Average	O(n^2)
   Worst	O(n^2)

2. Space Complexity: The space complexity of the selection sort algorithm is O(1).

Applications of Insertion Sort Algorithm

1. Small Datasets: Insertion Sort is efficient for sorting small datasets or lists with a small number of elements. It is faster than other sorting algorithms such as Merge Sort or Quick Sort when the input size is small.
2. Partially Sorted Arrays: If the input array is already partially sorted, insertion sort can be used to sort the remaining unsorted elements efficiently. This is because Insertion Sort has a linear time complexity when the input array is already sorted or almost sorted.
3. Online Algorithms: Insertion Sort is an online algorithm, which means it can sort a list as it receives it. This is useful in applications where the input data is continuously arriving, and sorting needs to be performed on the fly.
4. Adaptive Sorting: It quickly adapts to changes in the input data. For example, if the input data is almost sorted, then Insertion Sort can quickly identify this and sort the remaining unsorted elements efficiently.
5. In-Place Sorting: It sorts the input list without using any additional memory. This makes it ideal for sorting large datasets that cannot fit into memory.

Advantages of Insertion Sort Algorithm

1. Easy to implement: Insertion sort is easy to understand and implement compared to other complex sorting algorithms like quick sort or merge sort.
2. Space efficiency: Insertion sort has a space complexity of O(1) since it does not require any additional memory to sort the elements.
3. Adaptive: Insertion sort performs better on partially sorted arrays. This is because it can quickly detect when an element is in its correct position and move on to the next one, leading to faster sorting times.
4. Online sorting: It can sort data as it is received, without having to wait for all the data to be collected. This makes it useful in situations where data is continuously being generated, such as in live data streams or real-time data processing.
5. Best for small arrays: Insertion sort works well for small arrays with a few elements, where its simplicity and speed make it an optimal choice.
6. Stable: Insertion sort is a stable sorting algorithm, meaning that it maintains the relative order of equal elements in the sorted output as they were in the input.

Disadvantages of Insertion Sort Algorithm

1. Performance on large lists: Insertion sort has a time complexity of O(n^2) in the worst-case scenario, which makes it inefficient for large lists.
2. Not suitable for parallel processing: Insertion sort is an inherently sequential algorithm, which means it cannot take advantage of parallel processing. This makes it less suitable for high-performance computing applications where parallelism is important.
3. Less efficient than other sorting algorithms: Many other sorting algorithms are more efficient than insertion sort for large lists. For example, merge sort and quick sort have a time complexity of O(n log n), which makes them much faster than insertion sort for large lists.

Summary

So, here we saw every aspect of the insertion sort algorithm in data structures. It must not have been difficult to understand as it's one of the easiest sorting algorithms. Just make sure you are thorough with arrays in data structures. To apply your knowledge of the selection sort algorithm, enroll in our Best Data Structures And Algorithms Course.

Similar Sorting Algorithms

• Bubble Sort
• Merge Sort
• Quick Sort
• Selection Sort