What is Linear Search in Data Structures - Its Algorithm, Working, & Complexity

To further enhance your understanding and application of linear search concepts, consider enrolling in the best Best Dsa Course, where you can gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Linear Search in Data Structures?

Linear Search Algorithm

LinearSearch(array, key)
  for each item in the array
    if item == key
      return its index

1. Start at the first element of the list or array.
2. Compare the target value with the current element.
3. If the target value matches the current element, return the index of the current element and terminate the search.
4. If the target value does not match the current element, move to the next element in the list or array.
5. Repeat steps 2-4 until the target value is found or until every element has been checked.

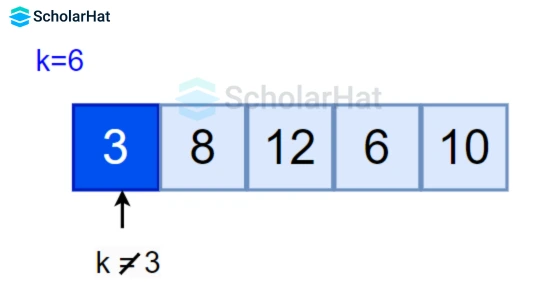
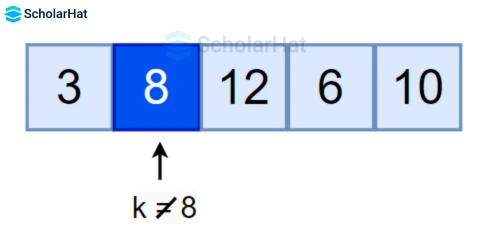
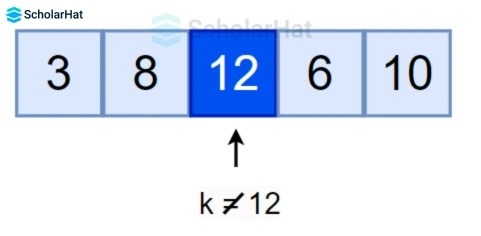
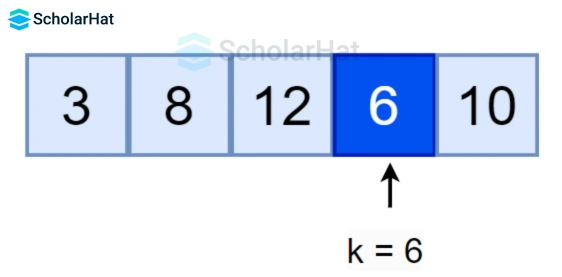
Working of Linear Search Algorithm in Data Structures

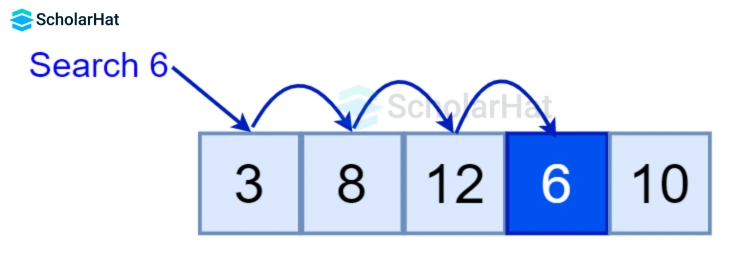
1. Start from the first element, and compare the key=6 with each element x.







2. If x == key, return the index.



3. Else, return not found.

Implementation of Linear Search Algorithm in Different Programming Languages

def search(array, key):
    # Going through the array sequentially
    for i in range(len(array)):
        if array[i] == key:
            return i
    return -1

array = [3, 8, 12, 6, 10, 2]
key = 6
print("The array to be searched is:", end=" ")
for value in array:
    print(value, end=",\t")
print()
print("The element to be searched:", key)

result = search(array, key)

if result == -1:
    print("Element not found")
else:
    print("Element found at index:", result)
    

public class LinearSearch {
    public static int search(int[] array, int key) {
        // Going through the array sequentially
        for (int i = 0; i < array.length; i++)
            if (array[i] == key)
                return i;
        return -1;
    }

    public static void main(String[] args) {
        int[] array = {3, 8, 12, 6, 10, 2};
        int key = 6;
        System.out.print("The array to be searched is: ");
        for (int value : array) {
            System.out.print(value + ",\t");
        }
        System.out.println();
        System.out.println("The element to be searched: " + key);

        int result = search(array, key);

        if (result == -1) {
            System.out.println("Element not found");
        } else {
            System.out.println("Element found at index: " + result);
        }
    }
}
    

#include <iostream>
using namespace std;

int search(int array[], int n, int key) {

  // Going through the array sequentially
  for (int i = 0; i < n; i++)
    if (array[i] == key)
      return i;
  return -1;
}

int main() {
  int array[] = {3, 8, 12, 6, 10, 2};
  int n = sizeof(array) / sizeof(array[0]);
  cout<< "The array to be searched is ";
    for (int i = 0; i < n; i++)
       cout << array[i] << "," << "\t"; 
   cout << endl; 
   int key = 6;
   cout << "The element to be searched: " << key << endl;
 
  int result = search(array, n, key);

  (result == -1) ? cout << "Element not found" : cout << "Element found at index: " << result;
}
    

Output

The array to be searched is 3,	8,	12,	6,	10,	2,	
The element to be searched: 6
Element found at index: 3  

Complexity Analysis of Linear Search Algorithm

1. Time Complexity

   Case	Time Complexity
   Best Case	O(1)
   Average Case	O(n)
   Worst Case	O(n)

2. Space Complexity: As we are not using any significant extra memory in linear search, the space complexity is constant, i.e. O(1).

When to use Linear Search?

1. Small Data Sets: Linear search works well with small data sets where the number of elements is relatively low.
2. Unsorted Data: Linear search is effective when the data is unsorted or the order of elements is not important. It sequentially checks each element until a match is found, regardless of the arrangement of elements.
3. Singly Linked Lists: Linear search is commonly used in singly linked lists where direct access to elements is not possible. It traverses the list one node at a time, making it a suitable choice for searching through linked structures.
4. Infrequent Searches: If searches are infrequent or the list is not frequently updated, linear search can be a straightforward and sufficient solution. It requires minimal setup and is easy to implement.
5. Educational Purposes: Linear search is often used as an introductory algorithm in programming and computer science courses to illustrate basic search concepts before moving on to more advanced algorithms.

Advantages of Linear Search

1. Simplicity: Linear search is a simple algorithm to understand and implement, making it easy to write and debug. It is an ideal algorithm to use when the list of items to be searched is small.
2. Efficient for small data sets: For small data sets, linear search can be more efficient than other search algorithms, such as binary search, due to the overhead associated with those algorithms.
3. Memory efficiency: Linear search requires minimal memory, making it a good choice for systems with limited memory resources.
4. Flexibility: Linear search can be used for unsorted lists, which makes it a useful algorithm for cases when the data is not sorted or when sorting the data is expensive or impossible.

Disadvantages of Linear Search

1. Time complexity: The worst-case time complexity of linear search is O(n), where n is the size of the array. This means that in the worst-case scenario, the linear search may have to check every element in the array, resulting in a time-consuming search operation. This makes linear search inefficient for large arrays, as the search time increases linearly with the size of the array.
2. Limited applicability: Linear search is not well-suited for searching sorted arrays, as binary search is a more efficient algorithm for this purpose.
3. Inefficient for multiple searches: If you need to perform multiple searches on the same array, a linear search can be inefficient, as it has to search the entire array every time. In contrast, other search algorithms like binary search can take advantage of a pre-sorted array to speed up subsequent searches.
4. Space complexity: Linear search has a space complexity of O(1), meaning it requires a constant amount of memory to perform the search. However, this can be a disadvantage if the array is very large, as it may not fit in memory.

Summary