What are the limitations of Linked List implementation of stacks

ulliTheres an extra requirement of memory due to the involvement of pointersliliRandom accessing of elements is not possible in a stackliul

Stack in Data Structures: Implementations in Java, Python, & C++

Q: Which implementation is best for stack

div1 Arraybased stackbrUsing an array as the underlying storage is one way to implement a stack This approach is simple and fast as both push and pop operations take constant timediv

Q: What is stack overflow and underflow

divUnderflow happens when we try to pop an item from an empty stack Overflow happens when we try to push more items on a stack than it can holddiv

04 Dec 2024

Beginner

28.4K Views

84 min read

Stack in Data Structures

A stack in data structures is a linear collection that follows the Last In, First Out (LIFO) principle, where the last element added is the first to be removed. This structure is essential in various algorithms and applications such as expression evaluation, backtracking, and memory management. Stack implementation can be done using different programming languages such as stack in data structures using C, and stack in data structures using Java, Each offers its unique advantages.

In this DSA tutorial, we will seethestackin datastructures in detaili.e. its features, working, implementation, etc.

What is a Stack in Data Structures?

A stack is an ordered list or we can say a container in which insertion and deletion can be done from the one end known as the top of the stack.
The last inserted element is available first and is the first one to be deleted.
Hence, it is known as Last In, First Out LIFO or First In, Last Out FILO.
In a stack, the element at the top is known as the top element.
When a new element is added to the stack, it is placed on top of the existing elements.
Stacks are dynamic; this means that they do not have a fixed size and their size can be increased or decreased depending upon the number of elements.

What is a Stack in Data Structures?

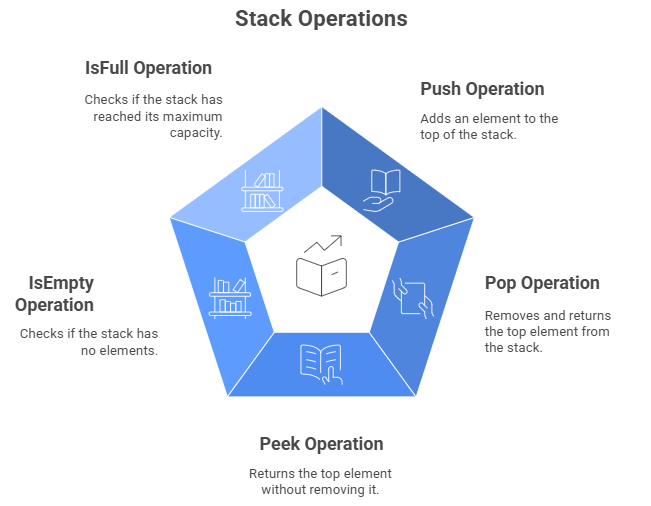
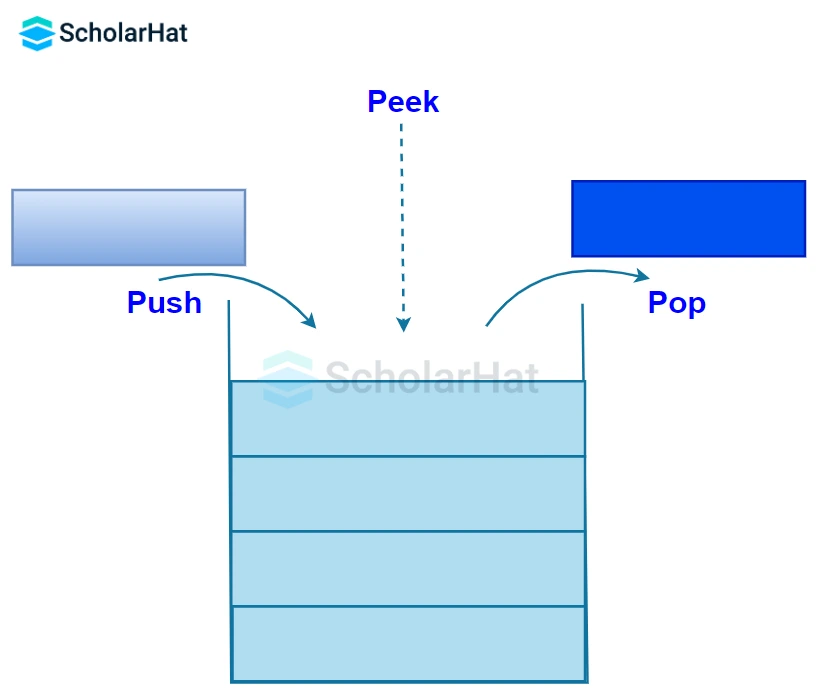
Standard Operations on Stack

Let's see the basic operations in the stack.The time complexity of all the given operations is constant, i.e. O(1).

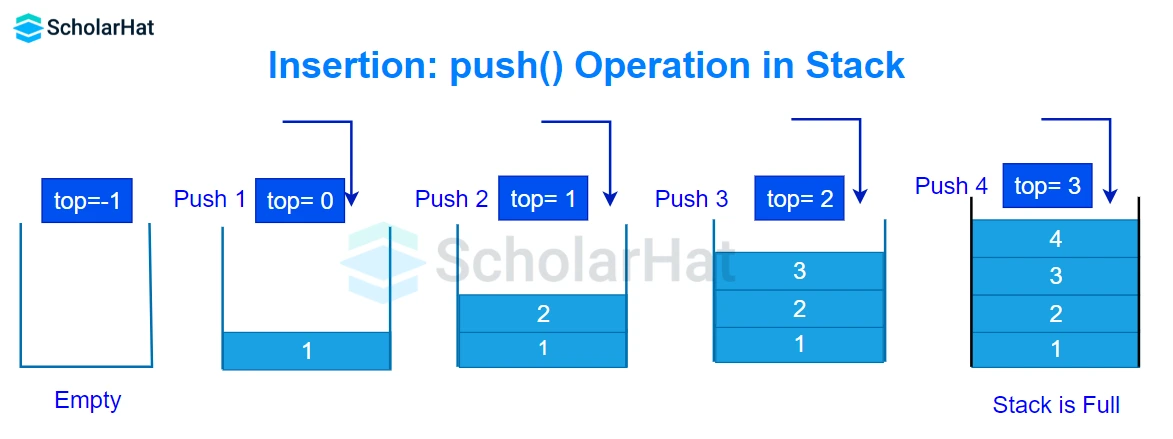
Insertion: push()

The push() operation is one of the fundamental operations in a stack data structure. Pushing means inserting an element at the top of the stack. If the stack is full, then it is said to be an Overflow condition.

Insertion: push() operation on stack

Algorithm for push() operation in the stack

begin
 if stack is full
 return
 endif
else 
 increment top
 stack[top] assign value
end else
end procedure

According to the algorithm,

First Check if the stack is full
If it is full, produce an error and exit
If the stack is not full, increment top to point to the next space.
Add the data element to the stack location, where the top is pointing.
End the process and exit.

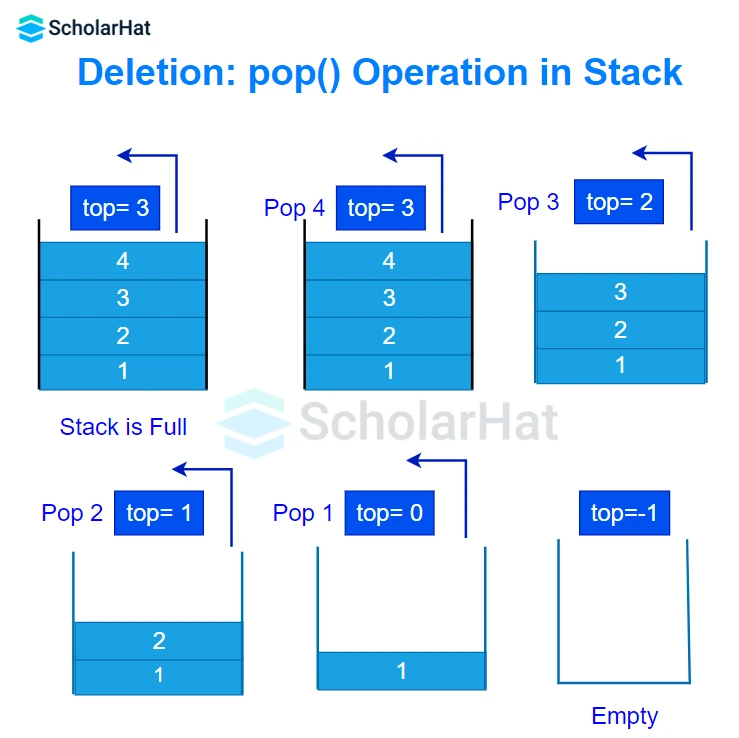
Deletion: pop()

The pop() operation is used to remove the topmost element of the stack and return its value. The pop() operation modifies the state of the stack by removing the topmost element. The items are popped in the reversed order in which they are pushed. If the Stack is empty, it is a Underflow condition.

Deletion: pop() in stack

Algorithm for pop() operation on the stack

begin
 if stack is empty
 return
 endif
else
 store value of stack[top]
 decrement top
 return value
end else
end procedure

According to the algorithm,

First, check if the stack is empty.
If empty, print Stack underflow and exit.
If not empty, access the data element at which the top is pointing.
Decrease the value of the top by 1.
End the process and exit.

peek()

The peek() operation returns the value of the topmost element of the stack without modifying the stack. This can be useful when you need to check the value of the top element before deciding whether to remove it or not.

peek() in java

Algorithm for peek() operation on the stack

begin 
 return stack[top]
end procedure

isFull()

The isFull() operation is used to determine if the stack is full or not. A stack is said to be full if it has reached its maximum capacity and there is no more space to add new elements to the stack.

Algorithm for isFull() operation on the stack

begin
 if stack length is equal to the maximum stack size
 return true
 endif
 else
 return false
 end else
end procedure

isEmpty()

The isEmpty() operation is used to check if the stack is empty or not. It returns a boolean value, true when the stack is empty, otherwise false.

Algorithm for isEmpty() operation on the stack

begin
 if top < 1
 return true
 else
 return false
end procedure

Working of Stack in Data Structures

The size of the stack depends on the number of memory blocks available to store the elements.

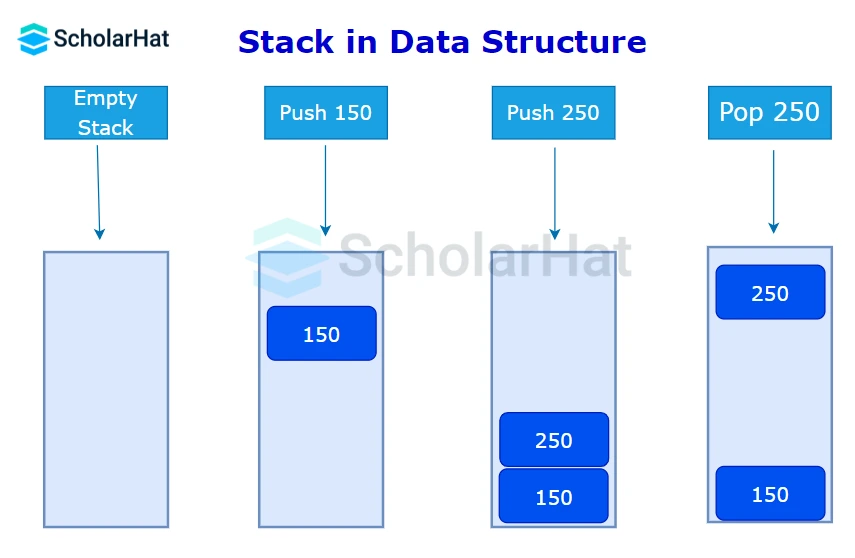
Initially, as shown in the figure, the stack is empty, and we can add elements one by one using the push operation until it becomes full.
A pointer called TOP is used to keep track of the top element in the stack.
When initializing the stack, we set its value to -1 so that we can check if the stack is empty by comparing TOP == -1.
On pushing an element, 150, we increase the value of TOP and place the new element in the position pointed to by TOP i.e. TOP=0 and so stack[0]=150.
Again we push n element, 250, and increase the value of TOP i.e. TOP=1 and so stack[1]=250.
On popping an element, we return the element pointed to by TOPi.e. return stack[1] and reduce its value i.e. TOP=0.
Before pushing, we check if the stack is already full.
Before popping, we check if the stack is already empty

Implementation of Stack in Different Programming Languages

There are two ways to implementStack in Data Structures, using a 1D Array and using a Single Linked List. Let us look at each of them.

The time complexity of all the operations in both implementations is the same i.e. O(1).

Implementation of Stack Using a 1D Array

Follow the below-given procedure to implement stack using a 1D Array in Data Structures

Declare a variable top to keep track of the top element in the stack.
When initializing the stack, set the value of the top to -1 Check if the stack is full or empty.
Declare a function push() that takes an array, stack[]; the size of the array, n; and element a is to be inserted as its parameters.
Under the function: you have to check if the stack is already full. If so, return from the function. and If the stack is not full, incrementtop and place the new element in the position pointed to by the top.

Declare a function pop() that removes the top element from the stack.
Under the function just check if the stack is empty. If so, return from the function then If the stack is not empty, return the element at the top index in the array stack[] and decrement top.Here, we are not deleting the value at the top index during pop() because once the pointer is moved to point to the previous element, it does not matter what is contained in that memory location.

Declare a function topElement() that returns the element at the top index from the array stack[].
Declare a function size() that returns the occupied size of the array stack[]. It returns top + 1.
Declare a function isEmpty() to check if the top is equal to -1. If it is, it returns true, otherwise false.
Declare a function isFull() to check if the top is equal to the maximum size of the array stack[]. If it is, it returns true, otherwise false.

Example of Stack Implementation in Different Languages using a 1D array


#include <iostream>
using namespace std;

class Stack {
private:
    int size;
    int* stack;
    int top;

public:
    Stack(int size) {
        this->size = size;
        stack = new int[size];
        top = -1;
    }

    void push(int a) {
        if (top == size - 1) {
            cout << "Stack Overflow" << endl;
        } else {
            stack[++top] = a;
        }
    }

    bool isEmpty() {
        return top == -1;
    }

    void pop() {
        if (isEmpty()) {
            cout << "Stack Underflow" << endl;
        } else {
            top--;
        }
    }

    int stackSize() {
        return top + 1;
    }

    int topElement() {
        return stack[top];
    }

    ~Stack() {
        delete[] stack;
    }
};

int main() {
    Stack stack(6);

    stack.push(5);
    cout << "Current size of stack is " << stack.stackSize() << endl;

    stack.push(10);
    stack.push(15);
    stack.push(20);
    stack.push(25);
    stack.push(30);
    cout << "Current size of stack is " << stack.stackSize() << endl;

    stack.push(35);
    cout << "At present, the top element in stack is " << stack.topElement() << endl;

    for (int i = 0; i < 6; ++i) {
        stack.pop();
    }
    cout << "Current size of stack is " << stack.stackSize() << endl;

    stack.pop();
    return 0;
}


using System;

class Stack {
    private int[] stack;
    private int top;
    private int size;

    public Stack(int size) {
        this.size = size;
        stack = new int[size];
        top = -1;
    }

    public void Push(int a) {
        if (top == size - 1) {
            Console.WriteLine("Stack Overflow");
        } else {
            stack[++top] = a;
        }
    }

    public bool IsEmpty() {
        return top == -1;
    }

    public void Pop() {
        if (IsEmpty()) {
            Console.WriteLine("Stack Underflow");
        } else {
            top--;
        }
    }

    public int StackSize() {
        return top + 1;
    }

    public int TopElement() {
        return stack[top];
    }
}

class Program {
    static void Main() {
        Stack stack = new Stack(6);

        stack.Push(5);
        Console.WriteLine("Current size of stack is " + stack.StackSize());

        stack.Push(10);
        stack.Push(15);
        stack.Push(20);
        stack.Push(25);
        stack.Push(30);
        Console.WriteLine("Current size of stack is " + stack.StackSize());

        stack.Push(35);
        Console.WriteLine("At present, the top element in stack is " + stack.TopElement());

        for (int i = 0; i < 6; i++) {
            stack.Pop();
        }
        Console.WriteLine("Current size of stack is " + stack.StackSize());

        stack.Pop();
    }
}


class Stack:
    def __init__(self, size):
        self.size = size
        self.stack = [-1] * size
        self.top = -1

    def push(self, a):
        if self.top == self.size - 1:
            print("Stack Overflow")
        else:
            self.top += 1
            self.stack[self.top] = a

    def is_empty(self):
        return self.top == -1

    def pop(self):
        if self.is_empty():
            print("Stack Underflow")
        else:
            self.top -= 1

    def stack_size(self):
        return self.top + 1

    def top_element(self):
        return self.stack[self.top]


if __name__ == "__main__":
    stack = Stack(6)

    stack.push(5)
    print("Current size of stack is", stack.stack_size())

    stack.push(10)
    stack.push(15)
    stack.push(20)
    stack.push(25)
    stack.push(30)
    print("Current size of stack is", stack.stack_size())

    stack.push(35)
    print("At present, the top element in stack is", stack.top_element())

    for _ in range(6):
        stack.pop()
    print("Current size of stack is", stack.stack_size())

    stack.pop()


class Stack {
    private int size;
    private int[] stack;
    private int top;

    public Stack(int size) {
        this.size = size;
        this.stack = new int[size];
        this.top = -1;
    }

    public void push(int a) {
        if (top == size - 1) {
            System.out.println("Stack Overflow");
        } else {
            stack[++top] = a;
        }
    }

    public boolean isEmpty() {
        return top == -1;
    }

    public void pop() {
        if (isEmpty()) {
            System.out.println("Stack Underflow");
        } else {
            top--;
        }
    }

    public int stackSize() {
        return top + 1;
    }

    public int topElement() {
        return stack[top];
    }
}

public class Main {
    public static void main(String[] args) {
        Stack stack = new Stack(6);

        stack.push(5);
        System.out.println("Current size of stack is " + stack.stackSize());

        stack.push(10);
        stack.push(15);
        stack.push(20);
        stack.push(25);
        stack.push(30);
        System.out.println("Current size of stack is " + stack.stackSize());

        stack.push(35);
        System.out.println("At present, the top element in stack is " + stack.topElement());

        for (int i = 0; i < 6; i++) {
            stack.pop();
        }
        System.out.println("Current size of stack is " + stack.stackSize());

        stack.pop();
    }
}


class Stack {
    private stack: number[];
    private top: number;
    private size: number;

    constructor(size: number) {
        this.size = size;
        this.stack = new Array(size).fill(-1);
        this.top = -1;
    }

    push(a: number): void {
        if (this.top === this.size - 1) {
            console.log("Stack Overflow");
        } else {
            this.top++;
            this.stack[this.top] = a;
        }
    }

    isEmpty(): boolean {
        return this.top === -1;
    }

    pop(): void {
        if (this.isEmpty()) {
            console.log("Stack Underflow");
        } else {
            this.top--;
        }
    }

    stackSize(): number {
        return this.top + 1;
    }

    topElement(): number {
        return this.stack[this.top];
    }
}

const stack = new Stack(6);

stack.push(5);
console.log("Current size of stack is", stack.stackSize());

stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
console.log("Current size of stack is", stack.stackSize());

stack.push(35);
console.log("At present, the top element in stack is", stack.topElement());

for (let i = 0; i < 6; i++) {
    stack.pop();
}
console.log("Current size of stack is", stack.stackSize());

stack.pop();

Output

Current size of stack is 1
Current size of stack is 6
Stack Overflow
At present, the top element in stack is 30
Current size of stack is 0
Stack Underflow

Advantages of Array Implementation

Easy to implement.
Memory is saved as pointers are not involved.

Limitations of Array Implementation

The maximum size of the array must be defined beforehand.
The size of the array cannot be changed during the run time because it is not dynamic.

Implementation of Stack Using a Single Linked List

Follow the below-given procedure to implement Stack using a Single Linked List in Data Structures.

First of all, create a class or structure Node with instance variables, data, and next.
The data will contain the element to be inserted and next will contain the address of the previous element in the linked list.
To keep track of the topmost element, create an instance, top of the class Node.
Declare a function push() that takes data as a parameter and adds it to the existing linked list.
Under the function –
- A temporary instance of the class Node is created, and memory is allocated for the same.
- Check if the heap is full. If it is, print Stack Overflow.
- If the heap is not full, add the data to the temporary instance.
Store the address of the previous top in the address part of the temporary instance.
Update the top so that it points to the temporary instance that contains the newly inserted value.
Declare a function pop() that deletes the currenttop, and point it to the element just before it.
Under the function –
- Check if the stack is empty or not. If it is, print Stack Underflow.
- If the stack is not empty, make the top point to the previous element.
- Free the memory that was used by the element that was popped.

Example of Stack Implementation in Different Languages Using a Single Linked List


#include <iostream>

class Node {
public:
    int data;
    Node* link;

    Node(int value) {
        data = value;
        link = nullptr;
    }
};

class Stack {
private:
    Node* top;

public:
    Stack() {
        top = nullptr;
    }

    void push(int data) {
        Node* temp = new Node(data);
        temp->link = top;
        top = temp;
    }

    bool isEmpty() {
        return top == nullptr;
    }

    int peek() {
        if (!isEmpty()) {
            return top->data;
        }
        throw std::runtime_error("Stack is empty");
    }

    void pop() {
        if (isEmpty()) {
            std::cerr << "Stack Underflow" << std::endl;
            exit(1);
        }
        Node* temp = top;
        top = top->link;
        delete temp;
    }
};

int main() {
    Stack stack;

    stack.push(5);
    stack.push(10);
    stack.push(15);
    stack.push(20);
    stack.push(25);
    stack.push(30);

    std::cout << "The Top element is " << stack.peek() << std::endl;

    stack.pop();
    stack.pop();
    stack.pop();
    stack.pop();
    stack.pop();

    std::cout << "The Top element is " << stack.peek() << std::endl;

    return 0;
}


using System;

class Node {
    public int Data;
    public Node Link;

    public Node(int value) {
        Data = value;
        Link = null;
    }
}

class Stack {
    private Node top;

    public Stack() {
        top = null;
    }

    public void Push(int data) {
        Node temp = new Node(data) {
            Link = top
        };
        top = temp;
    }

    public bool IsEmpty() {
        return top == null;
    }

    public int Peek() {
        if (!IsEmpty()) {
            return top.Data;
        }
        throw new InvalidOperationException("Stack is empty");
    }

    public void Pop() {
        if (IsEmpty()) {
            Console.WriteLine("Stack Underflow");
            Environment.Exit(1);
        }
        top = top.Link;
    }
}

class Program {
    static void Main(string[] args) {
        Stack stack = new Stack();

        stack.Push(5);
        stack.Push(10);
        stack.Push(15);
        stack.Push(20);
        stack.Push(25);
        stack.Push(30);

        Console.WriteLine("The Top element is " + stack.Peek());

        stack.Pop();
        stack.Pop();
        stack.Pop();
        stack.Pop();
        stack.Pop();

        Console.WriteLine("The Top element is " + stack.Peek());
    }
}


class Node:
    def __init__(self, data):
        self.data = data
        self.link = None

class Stack:
    def __init__(self):
        self.top = None

    def push(self, data):
        temp = Node(data)
        temp.link = self.top
        self.top = temp

    def is_empty(self):
        return self.top is None

    def peek(self):
        if not self.is_empty():
            return self.top.data
        raise Exception("Stack is empty")

    def pop(self):
        if self.is_empty():
            print("Stack Underflow")
            exit(1)
        self.top = self.top.link

if __name__ == "__main__":
    stack = Stack()

    stack.push(5)
    stack.push(10)
    stack.push(15)
    stack.push(20)
    stack.push(25)
    stack.push(30)

    print("The Top element is", stack.peek())

    stack.pop()
    stack.pop()
    stack.pop()
    stack.pop()
    stack.pop()

    print("The Top element is", stack.peek())


class Node {
    int data;
    Node link;

    Node(int value) {
        data = value;
        link = null;
    }
}

class Stack {
    private Node top;

    Stack() {
        top = null;
    }

    void push(int data) {
        Node temp = new Node(data);
        temp.link = top;
        top = temp;
    }

    boolean isEmpty() {
        return top == null;
    }

    int peek() {
        if (!isEmpty()) {
            return top.data;
        }
        throw new RuntimeException("Stack is empty");
    }

    void pop() {
        if (isEmpty()) {
            System.err.println("Stack Underflow");
            System.exit(1);
        }
        top = top.link;
    }
}

public class Main {
    public static void main(String[] args) {
        Stack stack = new Stack();

        stack.push(5);
        stack.push(10);
        stack.push(15);
        stack.push(20);
        stack.push(25);
        stack.push(30);

        System.out.println("The Top element is " + stack.peek());

        stack.pop();
        stack.pop();
        stack.pop();
        stack.pop();
        stack.pop();

        System.out.println("The Top element is " + stack.peek());
    }
}


class Node {
    data: number;
    link: Node | null;

    constructor(data: number) {
        this.data = data;
        this.link = null;
    }
}

class Stack {
    private top: Node | null;

    constructor() {
        this.top = null;
    }

    push(data: number): void {
        const temp = new Node(data);
        temp.link = this.top;
        this.top = temp;
    }

    isEmpty(): boolean {
        return this.top === null;
    }

    peek(): number {
        if (!this.isEmpty()) {
            return this.top!.data;
        }
        throw new Error("Stack is empty");
    }

    pop(): void {
        if (this.isEmpty()) {
            console.error("Stack Underflow");
            process.exit(1);
        }
        this.top = this.top!.link;
    }
}

const stack = new Stack();

stack.push(5);
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);

console.log("The Top element is", stack.peek());

stack.pop();
stack.pop();
stack.pop();
stack.pop();
stack.pop();

console.log("The Top element is", stack.peek());

Output

Top element is: 30
Top element is: 5

If you are facing any difficulty in understanding the linked list implementation of stack in data structures refer to the previous tutorial, Linked Lists in Data Structures.

Advantages of Linked List Implementation

A linked list is dynamic, i.e. the size of the linked list can be changed during the run time.
It is used in many virtual machines like JVM.

Limitations of Linked List Implementation

There's an extra memory requirement due to the involvement of pointers.
Random accessing of elements is not possible in a stack.

Problems On Stack

1. Implement Stack using Array

Problem: Write a program to implement a stack using a fixed-size array


#include <iostream>
using namespace std;

class Stack {
private:
    int* stack;
    int top;
    int size;

public:
    Stack(int s) {
        size = s;
        stack = new int[size];
        top = -1;
    }

    void push(int value) {
        if (top == size - 1) {
            cout << "Stack Overflow" << endl;
        } else {
            stack[++top] = value;
        }
    }

    void pop() {
        if (top == -1) {
            cout << "Stack Underflow" << endl;
        } else {
            top--;
        }
    }

    void display() {
        if (top == -1) {
            cout << "Stack is empty" << endl;
        } else {
            cout << "Stack elements: ";
            for (int i = 0; i <= top; i++) {
                cout << stack[i] << " ";
            }
            cout << endl;
        }
    }

    ~Stack() {
        delete[] stack;
    }
};

int main() {
    Stack s(5);
    s.push(10);
    s.push(30);
    s.display();
    s.pop();
    s.display();
    return 0;
}


using System;

class Stack {
    private int[] stack;
    private int top;
    private int size;

    public Stack(int s) {
        size = s;
        stack = new int[size];
        top = -1;
    }

    public void Push(int value) {
        if (top == size - 1) {
            Console.WriteLine("Stack Overflow");
        } else {
            stack[++top] = value;
        }
    }

    public void Pop() {
        if (top == -1) {
            Console.WriteLine("Stack Underflow");
        } else {
            top--;
        }
    }

    public void Display() {
        if (top == -1) {
            Console.WriteLine("Stack is empty");
        } else {
            Console.Write("Stack elements: ");
            for (int i = 0; i <= top; i++) {
                Console.Write(stack[i] + " ");
            }
            Console.WriteLine();
        }
    }
}

class Program {
    static void Main(string[] args) {
        Stack s = new Stack(5);
        s.Push(10);
        s.Push(30);
        s.Display();
        s.Pop();
        s.Display();
    }
}


class Stack:
    def __init__(self, size):
        self.size = size
        self.stack = []
    
    def push(self, value):
        if len(self.stack) == self.size:
            print("Stack Overflow")
        else:
            self.stack.append(value)
    
    def pop(self):
        if not self.stack:
            print("Stack Underflow")
        else:
            self.stack.pop()
    
    def display(self):
        if not self.stack:
            print("Stack is empty")
        else:
            print("Stack elements:", " ".join(map(str, self.stack)))

# Usage
s = Stack(5)
s.push(10)
s.push(30)
s.display()
s.pop()
s.display()


class Stack {
    private int[] stack;
    private int top;
    private int size;

    public Stack(int size) {
        this.size = size;
        stack = new int[size];
        top = -1;
    }

    public void push(int value) {
        if (top == size - 1) {
            System.out.println("Stack Overflow");
        } else {
            stack[++top] = value;
        }
    }

    public void pop() {
        if (top == -1) {
            System.out.println("Stack Underflow");
        } else {
            top--;
        }
    }

    public void display() {
        if (top == -1) {
            System.out.println("Stack is empty");
        } else {
            System.out.print("Stack elements: ");
            for (int i = 0; i <= top; i++) {
                System.out.print(stack[i] + " ");
            }
            System.out.println();
        }
    }
}

public class Main {
    public static void main(String[] args) {
        Stack s = new Stack(5);
        s.push(10);
        s.push(30);
        s.display();
        s.pop();
        s.display();
    }
}


class Stack {
    private stack: number[];
    private top: number;
    private size: number;

    constructor(size: number) {
        this.size = size;
        this.stack = [];
        this.top = -1;
    }

    push(value: number): void {
        if (this.stack.length === this.size) {
            console.log("Stack Overflow");
        } else {
            this.stack.push(value);
            this.top++;
        }
    }

    pop(): void {
        if (this.top === -1) {
            console.log("Stack Underflow");
        } else {
            this.stack.pop();
            this.top--;
        }
    }

    display(): void {
        if (this.top === -1) {
            console.log("Stack is empty");
        } else {
            console.log("Stack elements:", this.stack.join(" "));
        }
    }
}

// Usage
const s = new Stack(5);
s.push(10);
s.push(30);
s.display();
s.pop();
s.display();

Output

Stack elements: 10 20
Stack elements: 10

2. Check for Balanced Parentheses

Problem: Write a program to check if the given string of parentheses is balanced.


#include <iostream>
#include <stack>

bool isBalanced(const std::string &expression) {
    std::stack<char> stack;
    for (char ch : expression) {
        if (ch == '(' || ch == '{' || ch == '[') {
            stack.push(ch);
        } else if (ch == ')' || ch == '}' || ch == ']') {
            if (stack.empty()) return false;
            char top = stack.top();
            stack.pop();
            if ((ch == ')' && top != '(') ||
                (ch == '}' && top != '{') ||
                (ch == ']' && top != '[')) {
                return false;
            }
        }
    }
    return stack.empty();
}

int main() {
    std::cout << isBalanced("({[]})") << std::endl; // 1
    std::cout << isBalanced("([)]") << std::endl;   // 0
    return 0;
}


using System;
using System.Collections.Generic;

class Program {
    static bool IsBalanced(string expression) {
        Stack stack = new Stack();
        foreach (char ch in expression) {
            if (ch == '(' || ch == '{' || ch == '[') {
                stack.Push(ch);
            } else if (ch == ')' || ch == '}' || ch == ']') {
                if (stack.Count == 0) return false;
                char top = stack.Pop();
                if ((ch == ')' && top != '(') ||
                    (ch == '}' && top != '{') ||
                    (ch == ']' && top != '[')) {
                    return false;
                }
            }
        }
        return stack.Count == 0;
    }

    static void Main() {
        Console.WriteLine(IsBalanced("({[]})")); // True
        Console.WriteLine(IsBalanced("([)]"));   // False
    }
}


def is_balanced(expression):
    stack = []
    for char in expression:
        if char in "({[":
            stack.append(char)
        elif char in ")}]":
            if not stack:
                return False
            top = stack.pop()
            if char == ")" and top != "(":
                return False
            if char == "]" and top != "[":
                return False
            if char == "}" and top != "{":
                return False
    return not stack

print(is_balanced("({[]})"))  # True
print(is_balanced("([)]"))    # False


import java.util.Stack;

public class BalancedParentheses {
    public static boolean isBalanced(String expression) {
        Stack<Character> stack = new Stack<>();
        for (char ch : expression.toCharArray()) {
            if (ch == '(' || ch == '{' || ch == '[') {
                stack.push(ch);
            } else if (ch == ')' || ch == '}' || ch == ']') {
                if (stack.isEmpty()) return false;
                char top = stack.pop();
                if ((ch == ')' && top != '(') ||
                    (ch == '}' && top != '{') ||
                    (ch == ']' && top != '[')) {
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }

    public static void main(String[] args) {
        System.out.println(isBalanced("({[]})")); // true
        System.out.println(isBalanced("([)]"));   // false
    }
}


function isBalanced(expression: string): boolean {
    const stack: string[] = [];
    for (const char of expression) {
        if (char === '(' || char === '{' || char === '[') {
            stack.push(char);
        } else if (char === ')' || char === '}' || char === ']') {
            if (stack.length === 0) return false;
            const top = stack.pop();
            if ((char === ')' && top !== '(') ||
                (char === '}' && top !== '{') ||
                (char === ']' && top !== '[')) {
                return false;
            }
        }
    }
    return stack.length === 0;
}

console.log(isBalanced("({[]})")); // true
console.log(isBalanced("([)]"));   // false

Output

true
false

3. Next Greater Element

Problem: Given an array, find the next greater element for each element using a stack.


#include <iostream>
#include <vector>
#include <stack>
using namespace std;

vector nextGreaterElement(vector& arr) {
    vector result(arr.size(), -1);
    stack s;

    for (int i = 0; i < arr.size(); i++) {
        while (!s.empty() && arr[s.top()] < arr[i]) {
            result[s.top()] = arr[i];
            s.pop();
        }
        s.push(i);
    }

    return result;
}

int main() {
    vector arr1 = {4, 5, 2, 25};
    vector arr2 = {13, 7, 6, 12};

    vector result1 = nextGreaterElement(arr1);
    vector result2 = nextGreaterElement(arr2);

    for (int r : result1) cout << r << " ";
    cout << endl;

    for (int r : result2) cout << r << " ";
    cout << endl;

    return 0;
}


using System;
using System.Collections.Generic; // For Stack<int>

class Program {
    static int[] NextGreaterElement(int[] arr) {
        int[] result = new int[arr.Length];
        Array.Fill(result, -1);
        Stack<int> stack = new Stack<int>();

        for (int i = 0; i < arr.Length; i++) {
            while (stack.Count > 0 && arr[stack.Peek()] < arr[i]) {
                int idx = stack.Pop();
                result[idx] = arr[i];
            }
            stack.Push(i);
        }

        return result;
    }

    static void Main() {
        int[] arr1 = { 4, 5, 2, 25 };
        int[] arr2 = { 13, 7, 6, 12 };

        Console.WriteLine(string.Join(" ", NextGreaterElement(arr1))); // Output: 5 25 25 -1
        Console.WriteLine(string.Join(" ", NextGreaterElement(arr2))); // Output: -1 12 12 -1
    }
}


def next_greater_element(arr):
    stack = []
    result = [-1] * len(arr)

    for i in range(len(arr)):
        while stack and arr[stack[-1]] < arr[i]:
            idx = stack.pop()
            result[idx] = arr[i]
        stack.append(i)
    
    return result

print(next_greater_element([4, 5, 2, 25]))  # [5, 25, 25, -1]
print(next_greater_element([13, 7, 6, 12]))  # [-1, 12, 12, -1]


import java.util.Stack;

public class NextGreaterElement {
    public static int[] nextGreaterElement(int[] arr) {
        int[] result = new int[arr.length];
        Stack stack = new Stack<>();

        for (int i = 0; i < arr.length; i++) {
            result[i] = -1;
        }

        for (int i = 0; i < arr.length; i++) {
            while (!stack.isEmpty() && arr[stack.peek()] < arr[i]) {
                int idx = stack.pop();
                result[idx] = arr[i];
            }
            stack.push(i);
        }

        return result;
    }

    public static void main(String[] args) {
        int[] arr1 = {4, 5, 2, 25};
        int[] arr2 = {13, 7, 6, 12};

        for (int r : nextGreaterElement(arr1)) {
            System.out.print(r + " ");
        }
        System.out.println();

        for (int r : nextGreaterElement(arr2)) {
            System.out.print(r + " ");
        }
        System.out.println();
    }
}


function nextGreaterElement(arr: number[]): number[] {
    const stack: number[] = [];
    const result: number[] = new Array(arr.length).fill(-1);

    for (let i = 0; i < arr.length; i++) {
        while (stack.length > 0 && arr[stack[stack.length - 1]] < arr[i]) {
            const idx = stack.pop()!;
            result[idx] = arr[i];
        }
        stack.push(i);
    }

    return result;
}

console.log(nextGreaterElement([4, 5, 2, 25])); // [5, 25, 25, -1]
console.log(nextGreaterElement([13, 7, 6, 12])); // [-1, 12, 12, -1]

Output

5 25 25 -1
-1 12 12 -1

Applications of Stack

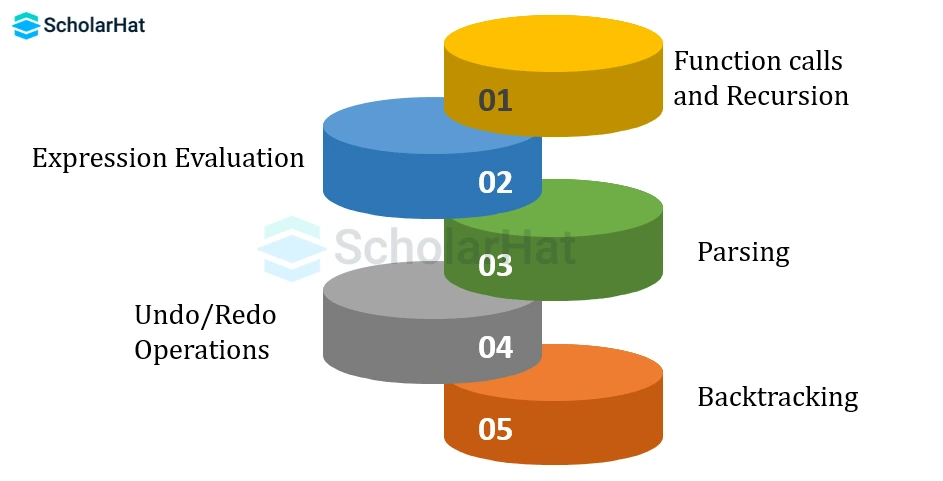
There are some applications of stacks in the data structure:

Function Calls and Recursion: When a function is called, the compiler stores information about the return address and the values of any parameters, in the stack. When the function is finished, the information is retrieved from the stack and the program continues executing from the point where it left off.
Recursion: To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained
Expression Evaluation: A stack can be used to evaluate arithmetic expressions in which parentheses are used to group sub-expressions. The operands and operators are pushed into the stack, and when a closing parenthesis is encountered, the sub-expression is evaluated using the operators and operands in the stack.
The A list of the expression conversion is given below:
- infix to prefix
- Infix to postfix
- Prefix to infix
- Prefix to postfix
- Postfix to infix
Parsing: A stack is often used in parsing algorithms to keep track of the nesting of symbols such as parentheses, brackets, and braces.
Undo/Redo Operations: Many applications, such as text editors and graphic design software, allow users to undo and redo previous operations. A stack can be used to store the state of the application before each operation, allowing the user to undo or redo the operation by popping or pushing elements from the stack.
Backtracking: When searching for a solution to a problem, it may be necessary to backtrack and try a different path if the current path does not lead to a solution. A stack can be used to store information about the current path, allowing the algorithm to backtrack by popping elements from the stack.

Advantages of Stack

Easy to implement: The implementation of a stack is simple, making it easy to use and understand.
Efficient memory management: A stack uses a contiguous block of memory, which is allocated when the stack is created. This makes it efficient in terms of memory utilization.
Accessibility: A stack allows quick access to its elements as the elements are added and removed from the top of the stack, which is useful in many applications, such as parsing expressions and reversing a string.
Recursive algorithms:A stack is used to store function calls and their states, which helps in the efficient implementation of recursive function calls.
Compiler Design: Stack is used in compiler design for parsing and syntax analysis of programming languages.

Disadvantages of Stack

Limited storage: Stacks can store only a fixed number of elements. In the case of stack overflow, there can be a loss of data.
No random access: Unlike other data structures like arrays, stacks do not provide direct access to elements in the middle of the stack. You can only add and remove elements from the top of the stack. The user has to remove all the elements above the middle element to access it.
Stack overflow and underflow: Adding or removing too many elements into and from the stack can cause stack overflow or underflow respectively causing the program to crash.
Memory management: Stack uses a contiguous block of memory, which can result in memory fragmentation or memory leaks if there's a frequent addition or removal of elements.

Summary

So, here we have studied every aspect of a stack in data structures. You might have got at least some idea regarding stack and its applications. I know it's quite difficult to understand the whole topic in a single go. Therefore, refer to it again and again till you get thorough with the stack in data structures. To grow your knowledge about the stack in data structures, enroll in our Data Structures and Algorithms.

FAQs

There's an extra requirement of memory due to the involvement of pointers.
Random accessing of elements is not possible in a stack.

1 Array-based stack
Using an array as the underlying storage is one way to implement a stack. This approach is simple and fast, as both push and pop operations take constant time.

Underflow happens when we try to pop an item from an empty stack. Overflow happens when we try to push more items on a stack than it can hold

01 Career Opportunities

02 Beginner

03 Intermediate

04 Advanced

05 Questions

06 Training Programs

Stack in Data Structures: Implementations in Java, Python, & C++

Free DSA Course with Certificate

Stack in Data Structures

What is a Stack in Data Structures?

Insertion: push()

Algorithm for push() operation in the stack

Deletion: pop()

Algorithm for pop() operation on the stack

peek()

Algorithm for peek() operation on the stack

isFull()

Algorithm for isFull() operation on the stack

isEmpty()

Algorithm for isEmpty() operation on the stack

Working of Stack in Data Structures

Implementation of Stack in Different Programming Languages

Implementation of Stack Using a 1D Array

Example of Stack Implementation in Different Languages using a 1D array

Output

Advantages of Array Implementation

Limitations of Array Implementation

Implementation of Stack Using a Single Linked List

Example of Stack Implementation in Different Languages Using a Single Linked List

Output

Advantages of Linked List Implementation

Limitations of Linked List Implementation

Problems On Stack

1. Implement Stack using Array

Output

2. Check for Balanced Parentheses

Output

3. Next Greater Element

Output

Applications of Stack

Advantages of Stack

Disadvantages of Stack

Summary

FAQs

Q1. What are the limitations of Linked List implementation of stacks?

Q2. Which implementation is best for stack?

Q3. What is stack overflow and underflow?

About Author

Live Batches Schedule View All