15
FebTower of Hanoi in Data Structures
Tower of Hanoi in Data Structures: An Overview
Tower of Hanoi is a mathematical game or puzzle that consists of three rods also called pegs and N number of disks of various diameters. These disks are arranged in ascending order from the top, the smallest at the top, thus approximating a conical shape. This puzzle is shifting all the given N number of disks from the source peg to the destination peg with the help of an alternate or auxiliary peg.
This DSA tutorial will discuss in detail the methods to solve the Tower of Hanoi problem. By 2027, 80% of coding interviews will focus on DSA skills. Ace them with our Free Data Structures and Algorithms Course today!
Problem Statement for Tower of Hanoi Problem
Move all the N number of disks from the given peg to the destination peg according to the simple rules mentioned below.
Tower of Hanoi Rules
- The game consists of three pegs and several disks of different sizes, which can slide onto any peg.
- The disks are initially placed on one peg in order of decreasing size so that the smallest disk is at the top and the largest disk is at the bottom.
- The objective of the game is to move the entire stack to another peg, obeying the following rules:
- Only one disk can be moved at a time.
- Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or an empty peg.
- No disk may be placed on top of a smaller disk.
- The puzzle can be solved in the minimum number of moves, which is (2^n)-1, where n is the number of disks.
- These rules apply to any version of the Tower of Hanoi puzzle, regardless of the number of pegs or disks used.
Constraints
- Number of pegs = 3 (source, auxiliary, destination).
- 1 <= N (Number of disks) < 100.
Example of working of Tower of Hanoi Algorithm
Let's assume the number of disks as N = 2. All three pegs are named A, B, and C. Our task is to shift the two disks from A to C using B. The stack is represented as follows:
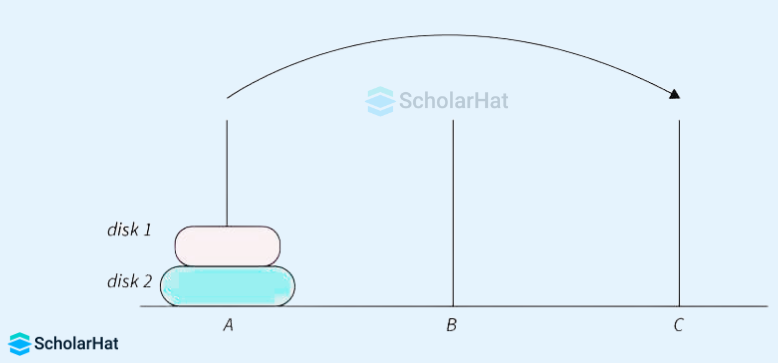
- Move disk 1 from peg A to peg B. After this move, the arrangement looks like this, which is shown in the below image.
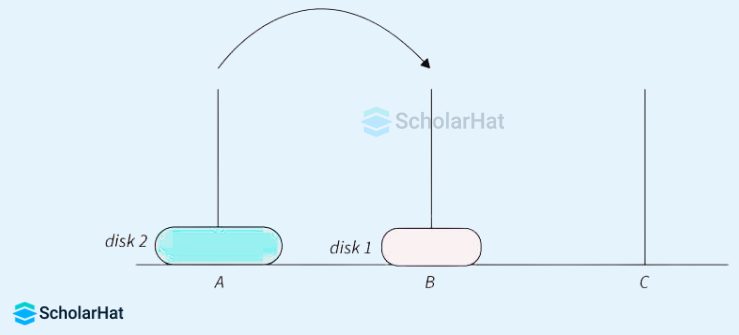
- Move disk 2 from peg A to peg C. After this move, the arrangement looks like this, which is shown in the below image.
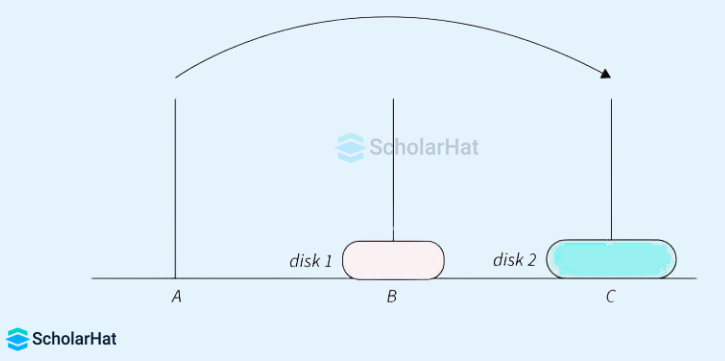
- Move disk 1 from peg B to peg C. After this move, the arrangement looks like this which is shown in the below image.
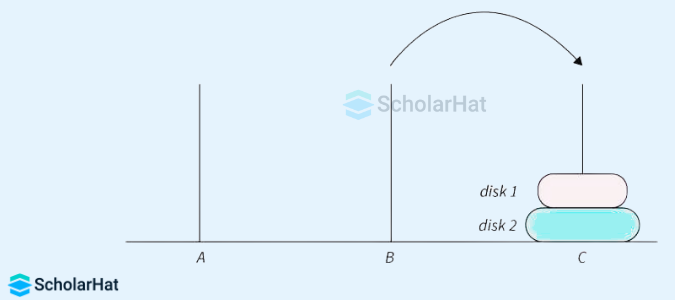
- From the above image, we can conclude that every disk is been moved from A (source peg) to C (destination peg) and this has been achieved by following the given rules which are mentioned above.
Read More - Data Structure Interview Questions for Experienced
Implementation of Tower of Hanoi Algorithm in Different Programming Languages
There are mainly two ways to implement the Tower of Hanoi Algorithm in Data Structures, using recursion and iteration. Let us look at each of them.
- Using Recursion
This approach mainly discusses the recursive approach to be followed for moving the disks from the source to the destination peg.
Recursive Tower of Hanoi Algorithm
Initially consider A as the source peg, B as the auxiliary peg, and C as the destination peg.
- Firstly, shift the n-1 number of disks from A to B, using C.
- Secondly, shift the last disk from A to C.
- The third step is to shift the n-1 number of disks from B to C, using A.
Example of Recursive Tower of Hanoi Algorithm in Different Languages
def TowerOfHanoi(N, source_rod, dest_rod, aux_rod):
# Base case: if N is 0, return
if N == 0:
return
# Calling the recursive function following the observed pattern
TowerOfHanoi(N - 1, source_rod, aux_rod, dest_rod)
# Printing the move that just happened
print(f"Move disk {N} from rod {source_rod} -> {dest_rod}")
# Calling the recursive function following the observed pattern
TowerOfHanoi(N - 1, aux_rod, dest_rod, source_rod)
# Driver code
if __name__ == "__main__":
# Number of disks in the given Tower of Hanoi
N = 3
# Calling the recursive function where 'A' -> source rod, 'C' -> destination rod, 'B' -> auxiliary rod
TowerOfHanoi(N, 'A', 'C', 'B')
public class TowerOfHanoi {
public static void towerOfHanoi(int N, char sourceRod, char destRod, char auxRod) {
// Base case: if N is 0, return
if (N == 0) {
return;
}
// Calling the recursive function following the observed pattern
towerOfHanoi(N - 1, sourceRod, auxRod, destRod);
// Printing the move that just happened
System.out.println("Move disk " + N + " from rod " + sourceRod + " -> " + destRod);
// Calling the recursive function following the observed pattern
towerOfHanoi(N - 1, auxRod, destRod, sourceRod);
}
public static void main(String[] args) {
// Number of disks in the given Tower of Hanoi
int N = 3;
// Calling the recursive function where 'A' -> source rod, 'C' -> destination rod, 'B' -> auxiliary rod
towerOfHanoi(N, 'A', 'C', 'B');
}
}
// C++ program for the Tower of Hanoi using recursion
#include
using namespace std;
void TowerOfHanoi(int N, char source_rod, char dest_rod, char aux_rod){
// Base case if n==0 return
if (N == 0){
return;
}
// calling the recursive function by following the pattern observed
TowerOfHanoi(N - 1, source_rod, aux_rod, dest_rod);
// printing the move which happened just
cout << "Move disk " << N << " from rod " << source_rod << " -> " << dest_rod << endl;
// calling the recursive function by following the pattern observed
TowerOfHanoi(N - 1, aux_rod, dest_rod, source_rod);
}
// Driver code
int main(){
// Number of disks in the given tower of Hanoi
int N = 3;
// calling the recursive function where A-> source rod, B-> auxiliary rod, C-> destination rod
TowerOfHanoi(N, 'A', 'C', 'B');
return 0;
}
Output
Move disk 1 from rod A -> C
Move disk 2 from rod A -> B
Move disk 1 from rod C -> B
Move disk 3 from rod A -> C
Move disk 1 from rod B -> A
Move disk 2 from rod B -> C
Move disk 1 from rod A -> C - Using Iteration
The iterative method is considered to be more optimal and only a few changes are to be made for the recursive approach to arrive at this solution.
- We need to calculate the total number of moves i.e. 2^(N-1), where N is the number of disks.
- Now, check if the number of disks N is even:
- If yes, then you need to interchange the destination pole and auxiliary pole.
- The pole is represented by stack k in the Tower of Hanoi problem.
- We use three different stacks for the r source peg, auxiliary peg, and destination peg.
- Now run a loop from i = 1 to the total number of moves i.e, 2^N because it involves 2^N to move from source to destination peg:
- if i%3 == 1:
- This means that there is an extra disk at the source pole that has to be moved to the source pole.
- Move the top disk from the source pole to the destination pole.
- if i%3 == 2:
- This means that there are two extra disks at the source pole which can be moved to the auxiliary pole.
- Move the top disk from the source pole to the auxiliary pole.
- if i%3 == 0:
- There is no extra disk on the source pole, so we need to follow the below step.
- Move the top disk from the auxiliary pole to the destination pole.
- if i%3 == 1:
Example of Iterative Tower of Hanoi Algorithm in Different Languages
class Stack:
def __init__(self, size):
self.size = size
self.top = -1
self.array = [0] * size
def create_stack(size):
return Stack(size)
def is_full(stack):
return stack.top == stack.size - 1
def is_empty(stack):
return stack.top == -1
def push(stack, element):
if is_full(stack):
return
stack.top += 1
stack.array[stack.top] = element
def pop(stack):
if is_empty(stack):
return float('-inf')
element = stack.array[stack.top]
stack.top -= 1
return element
def print_disk(source_rod, dest_rod, disk):
print(f"Move the disk {disk} from {source_rod} -> {dest_rod}")
def move_disks(src, dest, s, d):
pole1 = pop(src)
pole2 = pop(dest)
if pole1 == float('-inf'):
push(src, pole2)
print_disk(d, s, pole2)
elif pole2 == float('-inf'):
push(dest, pole1)
print_disk(s, d, pole1)
elif pole1 > pole2:
push(src, pole1)
push(src, pole2)
print_disk(d, s, pole2)
else:
push(dest, pole2)
push(dest, pole1)
print_disk(s, d, pole1)
def toh_iterative(N, src, aux, dest):
s, d, a = 'A', 'C', 'B'
if N % 2 == 0:
d, a = a, d
total_moves = pow(2, N) - 1
for i in range(N, 0, -1):
push(src, i)
for i in range(1, total_moves + 1):
if i % 3 == 1:
move_disks(src, dest, s, d)
elif i % 3 == 2:
move_disks(src, aux, s, a)
elif i % 3 == 0:
move_disks(aux, dest, a, d)
if __name__ == "__main__":
N = 3
source_rod = create_stack(N)
aux_rod = create_stack(N)
dest_rod = create_stack(N)
toh_iterative(N, source_rod, aux_rod, dest_rod)
class Stack {
int size;
int top;
int[] array;
public Stack(int size) {
this.size = size;
this.top = -1;
this.array = new int[size];
}
}
public class TowerOfHanoiIterative {
public static Stack createStack(int size) {
return new Stack(size);
}
public static boolean isFull(Stack stack) {
return stack.top == stack.size - 1;
}
public static boolean isEmpty(Stack stack) {
return stack.top == -1;
}
public static void push(Stack stack, int element) {
if (isFull(stack)) {
return;
}
stack.array[++stack.top] = element;
}
public static int pop(Stack stack) {
if (isEmpty(stack)) {
return Integer.MIN_VALUE;
}
return stack.array[stack.top--];
}
public static void printDisk(char sourceRod, char destRod, int disk) {
System.out.println("Move the disk " + disk + " from " + sourceRod + " -> " + destRod);
}
public static void moveDisks(Stack src, Stack dest, char s, char d) {
int pole1 = pop(src);
int pole2 = pop(dest);
if (pole1 == Integer.MIN_VALUE) {
push(src, pole2);
printDisk(d, s, pole2);
} else if (pole2 == Integer.MIN_VALUE) {
push(dest, pole1);
printDisk(s, d, pole1);
} else if (pole1 > pole2) {
push(src, pole1);
push(src, pole2);
printDisk(d, s, pole2);
} else {
push(dest, pole2);
push(dest, pole1);
printDisk(s, d, pole1);
}
}
public static void tohIterative(int N, Stack src, Stack aux, Stack dest) {
char s = 'A', d = 'C', a = 'B';
if (N % 2 == 0) {
char temp = d;
d = a;
a = temp;
}
int totalMoves = (int) Math.pow(2, N) - 1;
for (int i = N; i >= 1; i--) {
push(src, i);
}
for (int i = 1; i <= totalMoves; i++) {
if (i % 3 == 1) {
moveDisks(src, dest, s, d);
} else if (i % 3 == 2) {
moveDisks(src, aux, s, a);
} else if (i % 3 == 0) {
moveDisks(aux, dest, a, d);
}
}
}
public static void main(String[] args) {
int N = 3;
Stack sourceRod = createStack(N);
Stack auxRod = createStack(N);
Stack destRod = createStack(N);
tohIterative(N, sourceRod, auxRod, destRod);
}
}
#include
#include
using namespace std;
// Stack representation
struct Stack{
//initializing stack size, top
unsigned size;
int top;
int *array;
};
// function to create a stack of the given size.
struct Stack* Create_Stack(unsigned size){
struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
stack -> size = size;
// initialise top to -1
stack -> top = -1;
//dynamically allocating the memory for stack
stack -> array = (int*) malloc(stack -> size * sizeof(int));
return stack;
}
// Function to check whether stack is full
int Is_Full(struct Stack* stack){
// stack is full when top == size-1
return (stack->top == stack->size - 1);
}
// Function to check whether there tack is empty
int Is_Empty(struct Stack* stack){
// Stack is considered to be empty when top==-1
return (stack->top == -1);
}
// Function to add an item to stack. It increases top by 1
void push(struct Stack *stack, int element){
// if the stack is full you cannot add the item to the stack
if (Is_Full(stack))
return;
stack -> array[++stack -> top] = element;
}
// Function to remove an item from the stack. It decreases the top by 1
int pop(struct Stack* stack){
// if the stack is empty you cannot remove any
if (Is_Empty(stack))
return INT_MIN;
return stack -> array[stack -> top--];
}
//Function to show the movement of disks
void printdisk(char source_rod, char dest_rod, int disk){
cout <<"Move the disk " << disk <<" from " << source_rod << " -> "<< dest_rod << endl;
}
// Function to implement legal movement between two poles
void MoveDisks(struct Stack *src, struct Stack *dest, char s, char d){
int pole1 = pop(src);
int pole2 = pop(dest);
// When pole 1 is empty
if (pole1 == INT_MIN){
push(src, pole2);
// to print the movement which just happened
printdisk(d, s, pole2);
}
// When pole2 pole is empty
else if (pole2 == INT_MIN){
push(dest, pole1);
// to print the movement which justhappenedd
printdisk(s, d, pole1);
}
// When top disk of pole1 > top disk of pole2
else if (pole1 > pole2){
push(src, pole1);
push(src, pole2);
// to print the movement which just happend
printdisk(d, s, pole2);
}
// When top disk of pole1 < top disk of pole2
else{
push(dest, pole2);
push(dest, pole1);
// to print the movement which just happened
printdisk(s, d, pole1);
}
}
//Function to implement TOH puzzle
void TohIterative(int N, struct Stack *src, struct Stack *aux, struct Stack *dest){
int i, total_moves;
char s = 'A', d = 'C', a = 'B';
//If number of disks is even, then interchange the destination pole and auxiliary pole
if (N % 2 == 0){
char temp = d;
d = a;
a = temp;
}
total_moves = pow(2, N) - 1;
//Larger disks will be pushed first
for (i = N; i >= 1; i--)
push(src, i);
for (i = 1; i <= total_moves; i++){
if (i % 3 == 1)
MoveDisks(src, dest, s, d);
else if (i % 3 == 2)
MoveDisks(src, aux, s, a);
else if (i % 3 == 0)
MoveDisks(aux, dest, a, d);
}
}
// Driver Program
int main(){
// Total number of disks in the source peg
unsigned N = 3;
struct Stack *source_rod, *aux_rod, *dest_rod;
// Create three stacks to represent three pegs and of size number of disks to hold the disks
source_rod = Create_Stack(N);
aux_rod = Create_Stack(N);
dest_rod = Create_Stack(N);
// Calling the Tower of Hanoi iterative approach function
TohIterative(N, source_rod, aux_rod, dest_rod);
return 0;
}
Output
Move disk 1 from rod A -> C
Move disk 2 from rod A -> B
Move disk 1 from rod C -> B
Move disk 3 from rod A -> C
Move disk 1 from rod B -> A
Move disk 2 from rod B -> C
Move disk 1 from rod A -> C
Complexity Analysis of Tower of Hanoi Algorithm
| Time Complexity | Space Complexity | |
| Recursive Method | O(2^N) | O(N) |
| Iterative Method | O(N) | O(N) |
Here, N is the total number of disks.
Summary
The Tower of Hanoi is a fascinating brainteaser that can offer endless hours of fun and exercise for the mind. It presents both a mathematical challenge as well as an interesting strategy game requiring thought and planning to reach the end goal. While it may seem intimidating at first, it's not hard to understand the basic logic behind it, and with practice, many people have mastered this puzzle. To apply your knowledge, enroll in our Free Dsa Course.
With 18,000+ Java full stack jobs open in 2025, certified pros are in high demand. Secure your future with our Java full Stack Developer Course now!
FAQs
Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.