Understanding Trie Data Structure

What is Trie Data Structure ?

A Trie (pronounced try), also known as a Prefix Tree, is a tree-based data structure that is used to efficiently store and retrieve strings, especially when working with dictionaries or prefix-based searches.

• Each node in a Trie represents a character.
• A path from the root to a node represents a prefix of some string.
• The root node is empty and does not contain any character.
• Words with common prefixes share the same initial path, making the Trie memory-efficient for large datasets of wor

Unlike arrays or hash tables, which store words independently, a Trie organizes strings by their prefixes. This means that words with the same starting characters share the same path in the tree, reducing redundancy and improving lookup time.

Example: If we insert the words “cat”, “car”, and “cap”, the first two characters “ca” are stored only once, and the branching happens at the third character.

Key Features of Trie

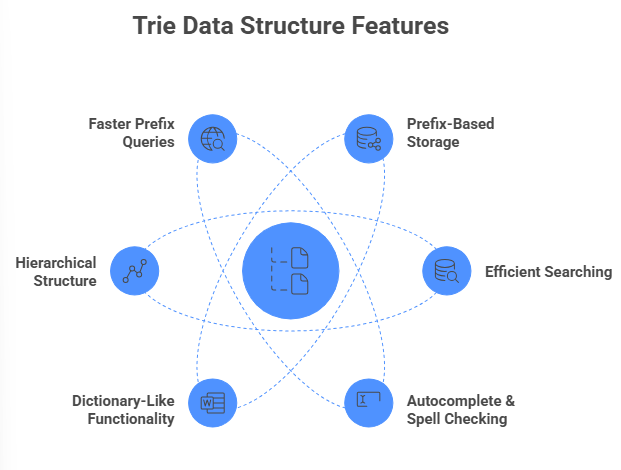
• Prefix-Based Storage: Common prefixes are stored once to reducing redundancy.
• Efficient Searching: Search, insert, and delete operations are performed in O(L) time, where L is the length of the word.
• Supports Autocomplete & Spell Checking: Ideal for applications like search engines, dictionaries, and word games.
• Dictionary-Like Functionality: Easily checks if a word or prefix exists in the dataset.
• Hierarchical Structure: Organizes data in a way that reflects the natural order of characters in strings.
• Faster than Hashing for Prefix Queries: Unlike hash tables, Tries efficiently handle prefix lookups and sorted order traversal of words.

Trie Structure Visualization

Let’s insert the words: cat, car, cap, bat

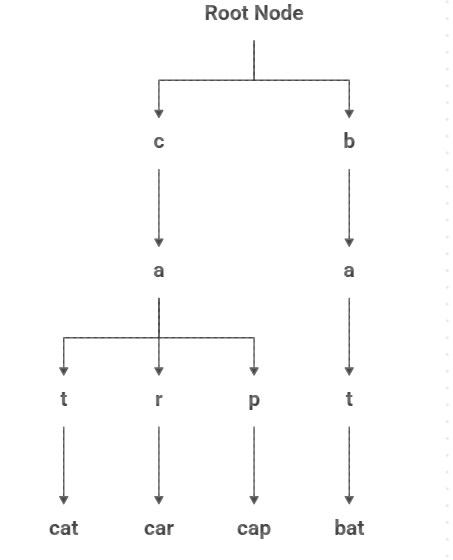
Explanation:

• The root node is empty.
• Under root, we have two branches: c (for words starting with c) and b (for words starting with b).
• From c → a, we have three different branches:

• From b → a → t, we get the word bat.

Java Implementation of Trie

import java.util.HashMap;
import java.util.Map;
class TrieNode {
    Map children = new HashMap<>();
    boolean isEndOfWord;
}
public class Trie {
    private TrieNode root;

    // Constructor
    public Trie() {
        root = new TrieNode();
    }

    // 1. Insert a word into Trie
    public void insert(String word) {
        TrieNode current = root;
        for (char ch : word.toCharArray()) {
            current = current.children.computeIfAbsent(ch, c -> new TrieNode());
        }
        current.isEndOfWord = true; // mark last node as end of word
    }

    // 2. Search for a word in Trie
    public boolean search(String word) {
        TrieNode current = root;
        for (char ch : word.toCharArray()) {
            TrieNode node = current.children.get(ch);
            if (node == null) {
                return false; // character path not found
            }
            current = node;
        }
        return current.isEndOfWord; // true if word exists completely
    }

    // 3. Check if any word starts with given prefix
    public boolean startsWith(String prefix) {
        TrieNode current = root;
        for (char ch : prefix.toCharArray()) {
            TrieNode node = current.children.get(ch);
            if (node == null) {
                return false;
            }
            current = node;
        }
        return true; // prefix exists
    }

    // 4. Delete a word from Trie
    public boolean delete(String word) {
        return delete(root, word, 0);
    }

    private boolean delete(TrieNode current, String word, int index) {
        if (index == word.length()) {
            if (!current.isEndOfWord) {
                return false; // word not found
            }
            current.isEndOfWord = false;
            return current.children.isEmpty(); // true if node can be deleted
        }
        char ch = word.charAt(index);
        TrieNode node = current.children.get(ch);
        if (node == null) {
            return false; // word not found
        }
        boolean shouldDeleteCurrentNode = delete(node, word, index + 1);

        if (shouldDeleteCurrentNode) {
            current.children.remove(ch);
            return current.children.isEmpty() && !current.isEndOfWord;
        }
        return false;
    }

    // --- Main Method for Testing ---
    public static void main(String[] args) {
        Trie trie = new Trie();

        // Insert words
        trie.insert("cat");
        trie.insert("car");
        trie.insert("cap");
        trie.insert("bat");

        // Search examples
        System.out.println(trie.search("car"));   // true
        System.out.println(trie.search("cab"));   // false

        // Prefix search
        System.out.println(trie.startsWith("ca")); // true
        System.out.println(trie.startsWith("do")); // false

        // Delete word
        trie.delete("car");
        System.out.println(trie.search("car"));   // false
        System.out.println(trie.search("cat"));   // true (still exists)
    }
}

Explanation of Code: Basic Operations in Trie

A Trie supports four primary operations: Insertion, Search, Deletion, and Prefix Matching. All of these operations typically take O(L) time, where L is the length of the word.

1. Insert Operation

public void insert(String word) {
    TrieNode current = root;
    for (char ch : word.toCharArray()) {
        current = current.children.computeIfAbsent(ch, c -> new TrieNode());
    }
    current.isEndOfWord = true; // mark last node as end of word
}

• We start from the root node.
• For each character in the word:
• If a child node for that character already exists → move to it.
• If not → create a new node using computeIfAbsent().
• After inserting all characters, mark the last node as isEndOfWord = true.

• c not in root → create new node.
• a not under c → create new node.
• r not under a → create new node.
• Mark r as end of word.

2. Search Operation

public boolean search(String word) {
    TrieNode current = root;
    for (char ch : word.toCharArray()) {
        TrieNode node = current.children.get(ch);
        if (node == null) {
            return false; // path not found
        }
        current = node;
    }
    return current.isEndOfWord; // must be a complete word
}

• Start at root and check each character in the word.
• If at any point a character path does not exist → return false.
• If traversal is successful, check if the final node is marked as isEndOfWord.

• Traverse → c → a → r
• r is marked as end of word → return true

• Traverse → c → a
• But a is not marked as end → return false

3. Prefix Search (startsWith)

public boolean startsWith(String prefix) {
    TrieNode current = root;
    for (char ch : prefix.toCharArray()) {
        TrieNode node = current.children.get(ch);
        if (node == null) {
            return false; // prefix not found
        }
        current = node;
    }
    return true; // prefix exists
}

Explanation:

• Similar to search, but we don’t care if the last node is marked as end of word.
• As long as all characters of the prefix are found, return true.

• Traverse → c → a
• Path exists → return true

• d not found at root → return false

4. Delete Operation

public boolean delete(String word) {
    return delete(root, word, 0);
}

private boolean delete(TrieNode current, String word, int index) {
    if (index == word.length()) {
        if (!current.isEndOfWord) {
            return false; // word not found
        }
        current.isEndOfWord = false;
        return current.children.isEmpty(); // true if node can be deleted
    }
    char ch = word.charAt(index);
    TrieNode node = current.children.get(ch);
    if (node == null) {
        return false; // word not found
    }
    boolean shouldDeleteCurrentNode = delete(node, word, index + 1);

    if (shouldDeleteCurrentNode) {
        current.children.remove(ch);
        return current.children.isEmpty() && !current.isEndOfWord;
    }
    return false;
}

• Recursive function that goes character by character.
• Base case: If end of word is reached → unmark isEndOfWord.
• Then check if the node has no children → it can be safely deleted.
• On the way back (recursion), remove unused nodes.

• Traverse c → a → r
• Unmark r as end of word.
• Since r has no children, delete r.
• Now ca still has t and p, so they remain.

Advantages of Trie

1. Efficient Prefix Searching

• Tries are designed for fast prefix lookups.
• Unlike hash tables, they can efficiently return words starting with a specific prefix.

2. Faster Search than Hashing for Large Datasets

• While hashing gives O(1) average search, it struggles with prefix-based queries and hash collisions.
• Tries maintain O(L) performance regardless of dataset size.

3. Dictionary Implementation

• Widely used for storing dictionaries, autocomplete systems, and spell checkers due to their ability to store words compactly with shared prefixes.

4. Memory Sharing via Prefixes

• Common prefixes are stored only once, which reduces memory usage for large datasets with many similar words.

5. Sorted Order Retrieval

• Tries naturally store keys in  order alphabetical order, making them useful for alphabetical listings.

Disadvantages of Trie

1. High Memory Usage

• Although prefixes are shared, each node can have multiple child references (up to 26 for English alphabets or more for Unicode), which increases memory usage compared to hash maps.

2. Complex Implementation

• More complex to implement than arrays, linked lists, or hash tables.

3. Space Wastage in Sparse Tries

• If only a few words are stored, many empty/null references are wasted, leading to inefficient memory usage.

4. Not Always Optimal for Small Data

• For small datasets or when prefix searching isn’t required, simpler data structures like hash maps or sets may perform better

Conclusion

The Trie Data Structure is highly efficient for string problems like prefix search, autocomplete, and dictionary lookups. By storing common prefixes once, it saves memory and speeds up searches, making it ideal for large-scale applications. While it may consume more memory for smaller datasets, Tries strike a strong balance between speed and efficiency, making them essential for coding interviews, competitive programming, and real-world systems.

90% of developers land jobs faster with DSA mastery – Solve 100+ problems in our Data Structure and Algorithm Course and get certified.

Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.

GET FREE CHALLENGE