A/B Testing for Machine Learning

Introduction

In data science for beginners, A/B testing is a powerful data science technique that assists organizations in optimizing their products and services and making data-driven decisions. A comparison of two variations, typically referred to as A and B, is necessary to determine which one performs better in terms of user engagement, conversion rates, or any other intended consequence. By allocating consumers at random to each version and then examining the results, this testing offers valuable insights into the effects of changes such as design modifications, feature additions, or pricing strategies.

What is A/B Testing?

A/B testing is a statistical method used in machine learning to assess and compare the performance of several models, algorithms, or iterations of a model. It entails dividing the data into more than one category and giving each group a unique variation or treatment. Based on specific requirements or objectives, the aim is to find out which version provides better results.

In A/B testing, the experimental group typically receives the new or modified version being evaluated, while the control group typically receives the current or baseline model. The only condition that differs for either group is the variant that is being tested. Data scientists can evaluate the effects of the modifications made in the group performing the experiment by comparing the results of both the control and the experimental groups.

Suitable metrics, including precision, recall, accuracy, and any other performance indicator appropriate for the particular problem, are used to assess each variant's performance. The observed variations in performance are next analyzed to ascertain whether they are statistically significant or the result of random chance, using statistical analytic techniques like hypothesis testing.

Data scientists can choose which model and algorithm variation to use for deployment and further optimization with the aid of A/B testing. It offers empirical data to assess the potency of various strategies and pinpoint the most effective solution.

A/B testing in machine learning

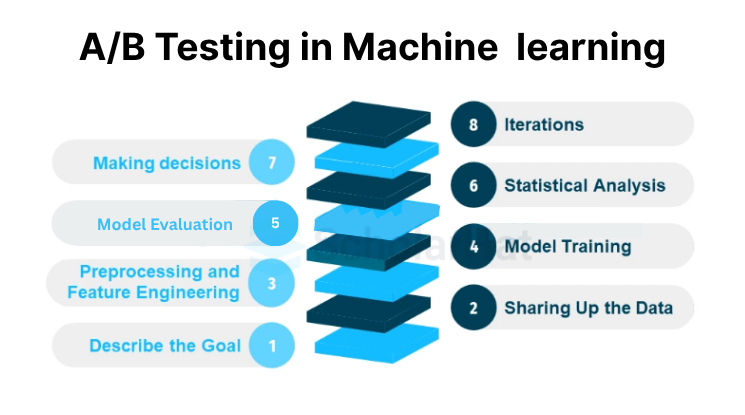
Machine learning can be used to evaluate and compare several models or algorithm iterations with the use of A/B testing. The machine learning process can include A/B testing in machine learning in the following ways:

• Describe the Goal: The A/B test's objective should be made very clear. It could entail increasing precision, optimizing a certain metric, or contrasting various models for a given task.
• Sharing Up the Data: Separate the dataset into two groups: an experimental group and a control group. In most cases, the experimental group is given the brand-new or modified variant under test, while the control group is given the baseline model or algorithm.
• Preprocessing and Feature Engineering To ensure fairness & comparability, apply the required feature engineering methods and preprocessing procedures uniformly to the experimental and control groups at the same time.
• Model Training: Using the appropriate datasets, train the experimental and control models. Make sure the training procedure is uniform, with the variant under test acting as the only variation.
• Model evaluation: Use the same evaluation criteria and test set to compare the performance of the two models. Compare performance indicators such as recall, accuracy, precision, or any other pertinent measures.
• Statistical Analysis: Use statistical methods to ascertain the significance of the variations between the experimental and control models that were observed. This aids in determining if the performance gains in the experimental version were caused by chance or were statistically significant.
• Making decisions: Make data-driven decisions in light of the A/B test outcomes. If the experimental variation shows statistically significant gains, deployment or additional refinement may be considered. Alternative strategies can be investigated in the alternative.
• A/B testing is a method that may involve iterations. Once a variation is chosen, it may be used as the new control and subsequent experiments with other alterations can be run to keep the model's performance improving.

A/B testing in machine learning models

A/B testing, usually referred to as split testing, is a method frequently employed in machine learning for comparing and evaluating the effectiveness of various models or variants of a model. It entails dividing the dataset into multiple groups of data and subjecting each group to a different model iteration or set of parameters. To ascertain whether a model and variation perform better in terms of particular metrics, like accuracy, precision, recall, and any other pertinent evaluation parameter, undergo a/b testing in machine learning models.

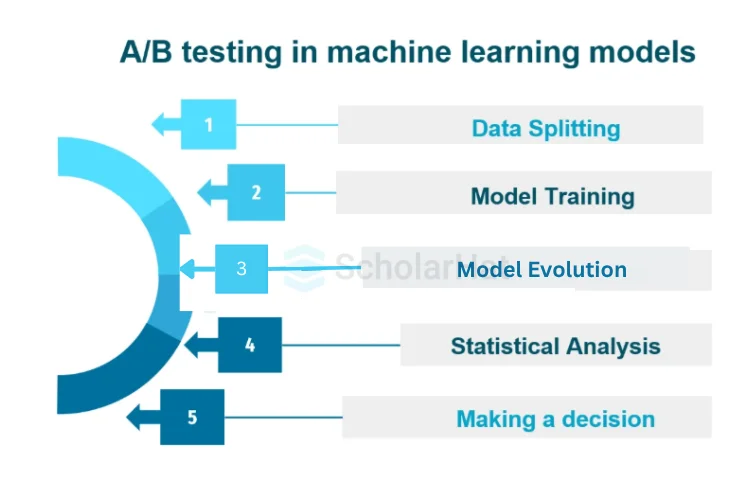
An outline of the process of A/B testing in machine learning models is provided below:

• Data Splitting: The dataset that is provided is split into several groups, usually two: the control group (A) & the treatment group (B). The group being treated is exposed to the new model or a variation of the baseline model, while the control group is subjected to the current or baseline model.
• Model Training: The appropriate models are trained using each group. While the treatment group trains the novel or variant model, the control group trains the baseline model. Using the training data, the model's parameters are optimized during the training phase.
• Model Evaluation: Using a common evaluation dataset and common evaluation metric(s), trained models are assessed. This dataset can be a holdover or a portion of the original dataset that wasn't used for training. Depending on the issue domain, the evaluation measure(s) may be accuracy, precision, recall, F1-score, or any other pertinent parameter.
• Statistical Analysis: Statistical analysis is done to compare the effectiveness of the models. Confidence intervals, hypothesis testing, and resampling procedures are typical techniques. The objective is to establish whether the observed performance differences are statistically significant and not the result of chance.
• Making a decision: Choosing the better-performing model is decided upon based on the statistical analysis. This choice can entail implementing the new model, altering the current model in light of the new model's findings, or conducting additional research and testing.

Summary

A statistical method called AB testing is used in machine learning to assess and contrast several models or algorithm iterations. It entails dividing data into control & experimental groups, with the experimental group receiving a novel variant under test while the control group receives the current model or algorithm. Data scientists can choose the best model and optimize it by comparing the performance of different groups using particular criteria.

Setting the aim and creating hypotheses is the first step in the AB testing process. On comparable datasets, controlled tests are carried out, and the effectiveness of each version is assessed and contrasted using the right metrics. Techniques of statistical analysis are used to assess the importance of differences that have been noticed.

A/B testing offers a structured and empirical method for model assessment and improvement. It guarantees that judgments are based on factual information rather than conjecture. Organizations may enhance the performance and efficacy of their machine learning models, producing better results in practical applications, by utilizing the insights provided via AB testing.

Splitting the data, feature engineering, model training, model evaluation, statistical analysis, and decision-making are just a few of the processes that go into incorporating AB testing into the machine learning workflow. By choosing promising versions and running additional experiments, the iterative method enables continual improvements.

Data scientists may choose the best models for deployment, conduct continuous model performance improvement based on empirical data, and make data-driven decisions by using AB testing in machine learning. The reliability and efficiency of machine learning systems in addressing real-world issues are ensured by AB testing.