Trees in Data Structures - Its Structure, Operations & Applications

24 Jun 2024

Advanced

4.34K Views

55 min read

Trees in Data Structures: An Overview

We saw in the first tutorial, Data Structures and its Types, a Tree is a type of non-primitive and non-linear data structure consisting of a hierarchy of nodes and a set of edges connecting them. In this DSA tutorial, we will see a detailed starting of the tree concept i.e. its features, types, implementation, etc.

To further enhance your understanding and application of graph concepts, consider enrolling in the best Data Structures and Algorithms Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is a Tree Data Structure?

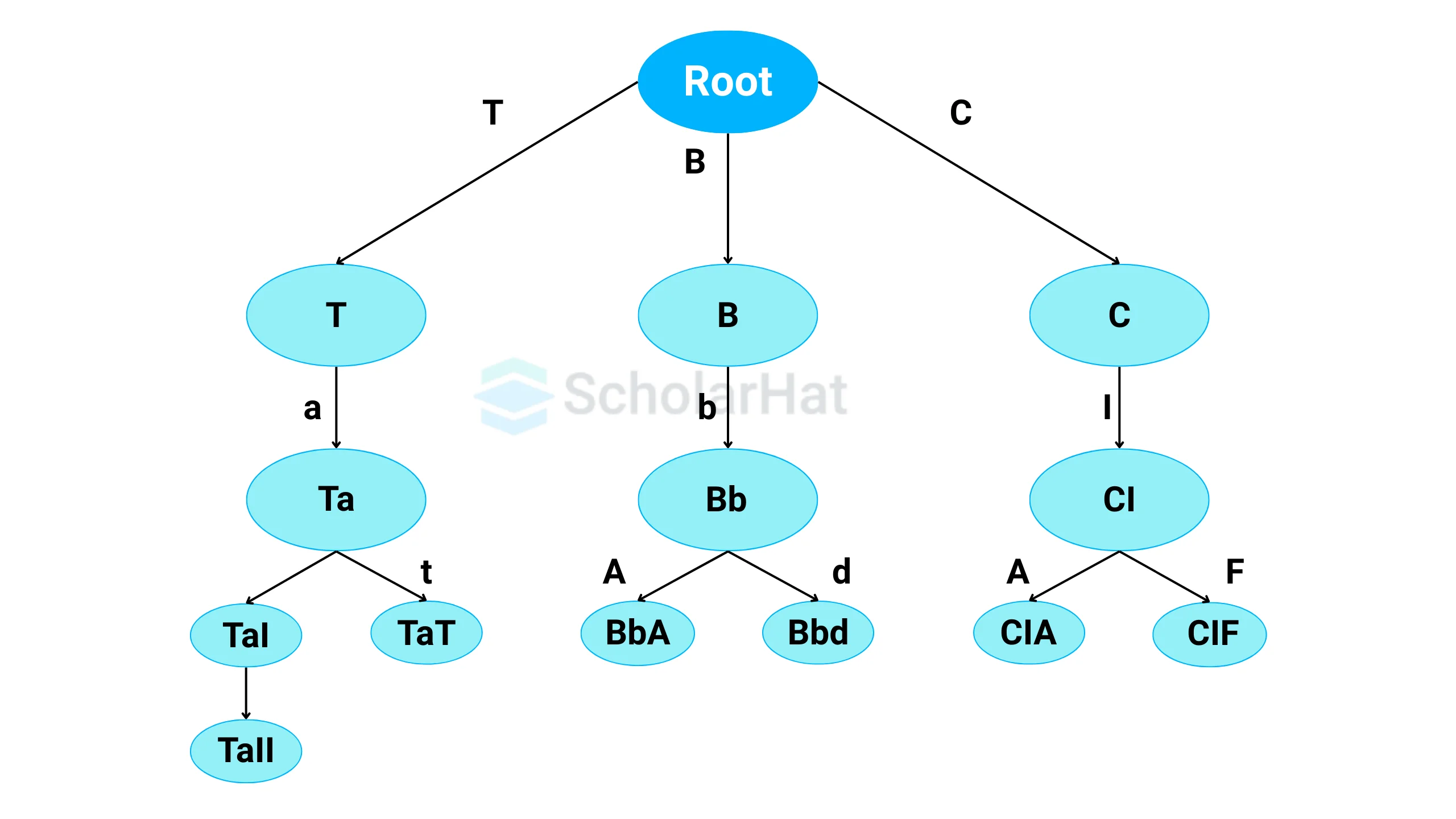
A tree in data structures is a collection of objects or entities known as nodes that are connected by edges and have a hierarchical relationship between the nodes.

The topmost node of the tree is called the root node from which the tree originates, and the nodes below it are called the child nodes. Each node can have multiple child nodes, and these child nodes can also have their child nodes, forming a recursive structure. Hence, we can also say that the tree data structure has roots, branches, and leaves connected. Each node contains some value and also list of references to child nodes.

Terminologies in Tree Data Structure

Terminology	Description	Diagram
Root	The topmost node of a tree. It does not have a parent	Node Root
Parent Node	An immediate predecessor of any node	T is the parent of Ta
Child Node	All immediate successors of a node	Tal and Tat are children of Ta
Leaf	Node which does not have any child	Tat, BbA, Bbd, CIA, and CIF are the leaf nodes
Edge	It is the link between any two nodes. In a tree with n nodes, there will be n-1 edges in a tree.	Eg. the connecting line between Root and T
Siblings	Children of the same parent node	Tal and Tat are siblings
Path	number of successive edges from the source node to the destination node.	Root, B, Bb, Bbd is a path from node Root to Bbd
Height of a Node	The number of edges on the longest path between that node and a leaf.	Root, B, Bb, Bbd form a height. The height of Root is no. of edges between A and Bbd, which is 3. Similarly, the height of Bb is 1 as it has just one edge until the next leaf node.
Degree of a Node	The total number of branches of that node or the number of child nodes a node has.	The degree of T is 4 and of B is 3
Depth of a node	the number of edges in the path from the root of the tree to the node.	The depth of the Bb node is 2
Height of the Tree	length of the longest path from the root of the tree to a leaf node of the tree.	The height of the above tree is 4
Internal Node	A node that has at least one child	All the nodes except Tat, BbA, Bbd, CIA, and CIF are internal
Ancestor node	all the predecessor nodes from the root until that node	Root, B, and Bb are ancestors of BbA and Bbd
Descendant	Immediate successor of a node	Bbd is the descendant of Bb
Sub tree	Descendants of a node represent a subtree.	B, Bb, Bbd, and BbA represent one sub-tree
Level of a node	count of edges on the path from the root node to that node.

Representation of a Tree in Data Structures

A tree consists of a root, and zero or more subtrees such that there is an edge from the root of the tree to the root of each subtree.

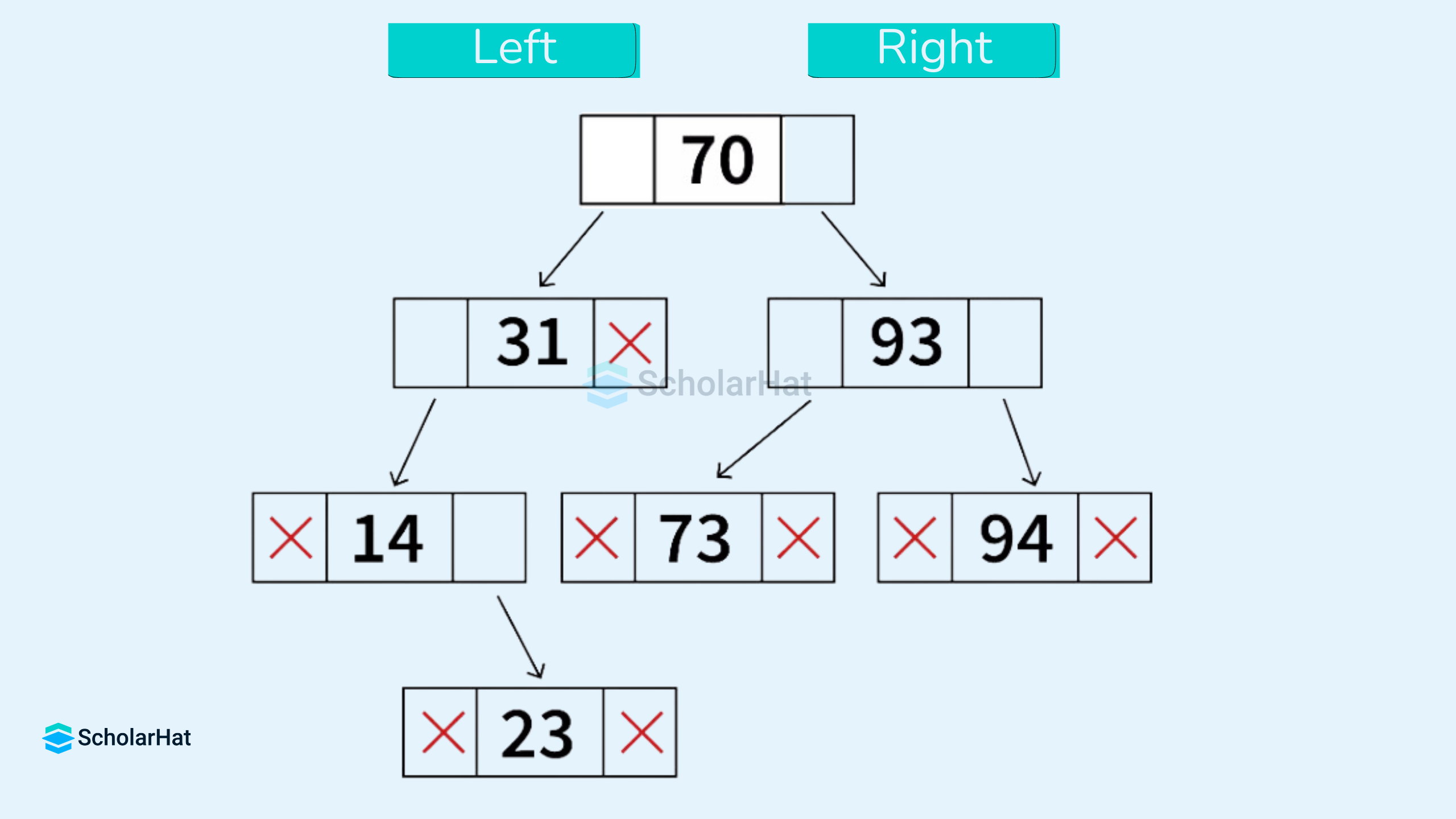
Each node consists of three fields. The left part of the node consists of the memory address of the left child, the right part of the node consists of the memory address of the right child, and the center part holds the data for this node.

How to declare/create a Tree in Data Structures?

struct node {
    int data;
    struct node* left;
    struct node* right;
}

Here left will contain the reference to the Node that has a value that is just smaller than the value in the current Node. Similarly right will contain a reference to the Node that has a value greater than the current Node.

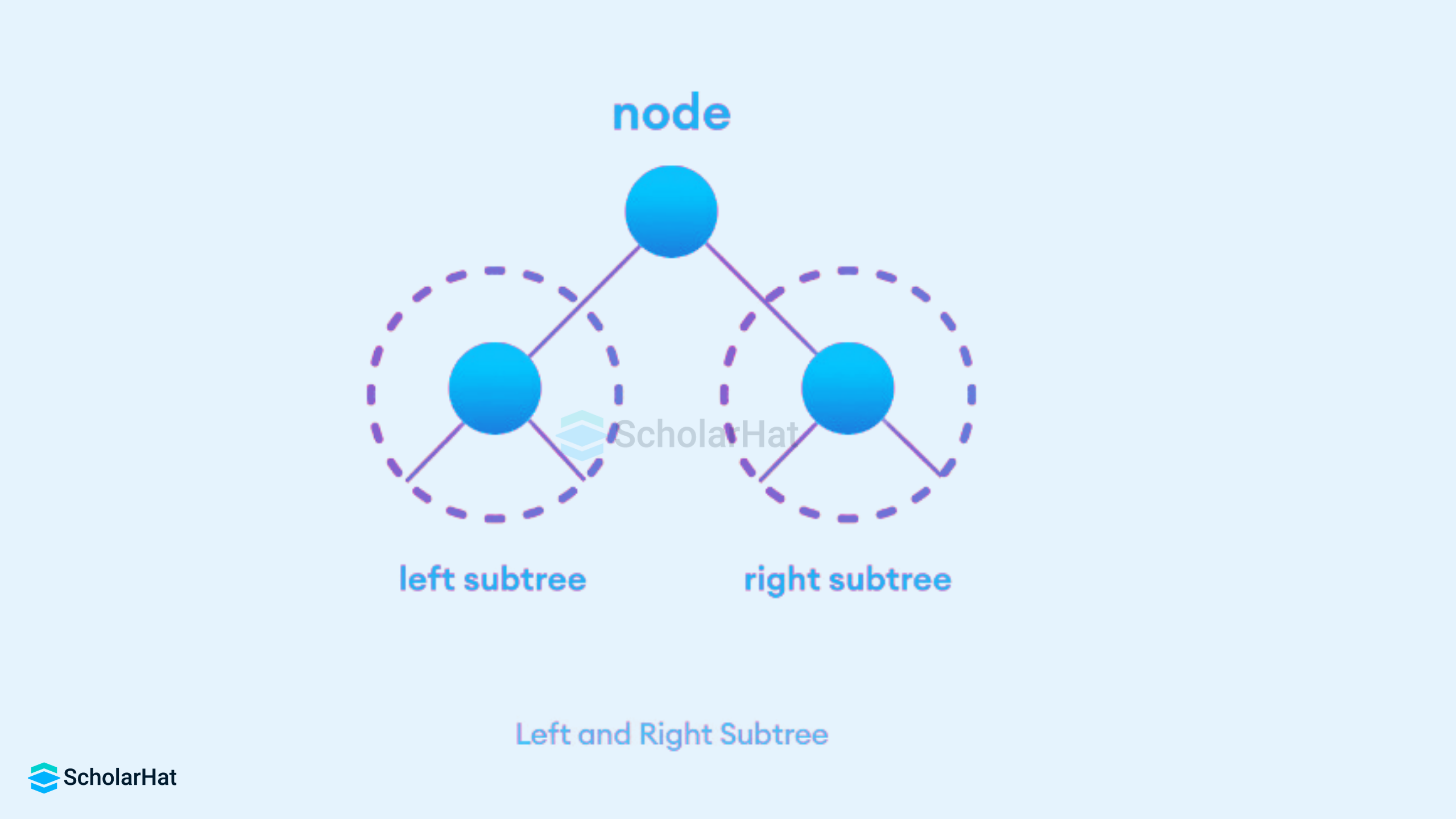
The struct node pointed to by left and right might have other left and right children so we should think of them as sub-trees instead of sub-nodes. Therefore, every tree is a combination of

A node carrying data
Two subtrees

Types Of Trees in Data Structures

Standard Operations on Trees in Data Structures

Traversal

Traversing a tree means visiting every node in the tree. A tree can be traversed in different ways, unlike linear data structures like arrays, stacks, queues, and linked lists. Depending on the order in which we do this, there can be three types of traversal.

Inorder Traversal: For this,
1. First, visit all the nodes in the left subtree
2. Then the root node
3. Visit all the nodes in the right subtree
```
inorder(root->left)
display(root->data)
inorder(root->right)
```
Preorder Traversal: For this,
1. Visit root node
2. Visit all the nodes in the left subtree
3. Visit all the nodes in the right subtree
```
display(root->data)
preorder(root->left)
preorder(root->right)
```
Postorder Traversal: For this,
1. Visit all the nodes in the left subtree
2. Visit all the nodes in the right subtree
3. Visit the root node
```
postorder(root->left)
postorder(root->right)
display(root->data)
```

Example of Tree Traversal in Tree Data Structure


class Node:
    def __init__(self, item):
        self.left = None
        self.right = None
        self.val = item


def inorder(root):
    if root:
        # Traverse left
        inorder(root.left)
        # Traverse root
        print(str(root.val) + "->", end='')
        # Traverse right
        inorder(root.right)


def postorder(root):
    if root:
        # Traverse left
        postorder(root.left)
        # Traverse right
        postorder(root.right)
        # Traverse root
        print(str(root.val) + "->", end='')


def preorder(root):
    if root:
        # Traverse root
        print(str(root.val) + "->", end='')
        # Traverse left
        preorder(root.left)
        # Traverse right
        preorder(root.right)


def print_tree(root, level=0, prefix="Root: "):
    if root:
        print(" " * (level * 4) + prefix + str(root.val))
        if root.left or root.right:
            print_tree(root.left, level + 1, "L--- ")
            print_tree(root.right, level + 1, "R--- ")


root = Node(1)
root.left = Node(6)
root.right = Node(8)
root.left.left = Node(4)
root.left.right = Node(5)

print("Tree Structure:")
print_tree(root)

print("\nInorder traversal:")
inorder(root)

print("\nPreorder traversal:")
preorder(root)

print("\nPostorder traversal:")
postorder(root)


class Node {
    int val;
    Node left, right;

    public Node(int item) {
        val = item;
        left = right = null;
    }
}

public class TreeTraversal {
    Node root;

    void inorder(Node root) {
        if (root != null) {
            inorder(root.left);
            System.out.print(root.val + "->");
            inorder(root.right);
        }        
    }

    void postorder(Node root) {
        if (root != null) {
            postorder(root.left);
            postorder(root.right);
            System.out.print(root.val + "->");
        }
    }

    void preorder(Node root) {
        if (root != null) {
            System.out.print(root.val + "->");
            preorder(root.left);
            preorder(root.right);
        }
    }

    void printTree(Node root, int level, String prefix) {
        if (root != null) {
            System.out.println(" ".repeat(level * 4) + prefix + root.val);
            if (root.left != null || root.right != null) {
                printTree(root.left, level + 1, "L--- ");
                printTree(root.right, level + 1, "R--- ");
            }
        }
    }

    public static void main(String[] args) {
        TreeTraversal tree = new TreeTraversal();
        tree.root = new Node(1);
        tree.root.left = new Node(6);
        tree.root.right = new Node(8);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);

        System.out.println("Tree Structure:");
        tree.printTree(tree.root, 0, "Root: ");
        
        System.out.println();
        
        System.out.println("Inorder traversal:");
        tree.inorder(tree.root);
        
        System.out.println();
        
        System.out.println("Preorder traversal:");
        tree.preorder(tree.root);
        
        System.out.println();
        
        System.out.println("Postorder traversal:");
        tree.postorder(tree.root);
    }
}


#include 
#include 

using namespace std;

class Node {
public:
    int val;
    Node *left, *right;

    Node(int item) {
        val = item;
        left = right = nullptr;
    }
};

class TreeTraversal {
public:
    Node *root;

    void inorder(Node *root) {
        if (root != nullptr) {
            inorder(root->left);
            cout << root->val << "->";
            inorder(root->right);
        }
    }

    void postorder(Node *root) {
        if (root != nullptr) {
            postorder(root->left);
            postorder(root->right);
            cout << root->val << "->";
        }
    }

    void preorder(Node *root) {
        if (root != nullptr) {
            cout << root->val << "->";
            preorder(root->left);
            preorder(root->right);
        }
    }

    void printTree(Node *root, int level, string prefix) {
        if (root != nullptr) {
            cout << string(level * 4, ' ') << prefix << root->val << endl;
            if (root->left != nullptr || root->right != nullptr) {
                printTree(root->left, level + 1, "L--- ");
                printTree(root->right, level + 1, "R--- ");
            }
        }
    }
};

int main() {
    TreeTraversal tree;
    tree.root = new Node(1);
    tree.root->left = new Node(6);
    tree.root->right = new Node(8);
    tree.root->left->left = new Node(4);
    tree.root->left->right = new Node(5);

    cout << "Tree Structure:" << endl;
    tree.printTree(tree.root, 0, "Root: ");

    cout << "\nInorder traversal:" << endl;
    tree.inorder(tree.root);

    cout << "\nPreorder traversal:" << endl;
    tree.preorder(tree.root);

    cout << "\nPostorder traversal:" << endl;
    tree.postorder(tree.root);

    return 0;
}

Output

Tree Structure:
Root: 1
    L--- 6
        L--- 4
        R--- 5
    R--- 8

Inorder traversal:
4->6->5->1->8->
Preorder traversal:
1->6->4->5->8->
Postorder traversal:
4->5->6->8->1->

Insertion

Insertion is the process of adding a new node to a tree. It involves finding the appropriate position for the new node and connecting it to the existing structure. The specific insertion steps depend on the tree type and the rules or constraints it follows.

Process of insertion in a tree

Start at the root of the Tree.
Initialize a variable currentNode to point to the root.
For each character in the string to be inserted, do the following:
- Check if the current character is already a child of the currentNode. If yes, update the currentNode to the child node corresponding to the current character.
- If the current character is not a child of the currentNode, create a new TreeNode for the character and add it as a child of the currentNode.
- Update currentNode to the newly created child node.
- After inserting all the characters, mark the last node as the end of a word (e.g., by setting a flag or attribute).


class TreeNode:
    def __init__(self):
        self.children = {}
        self.isEndOfWord = False


def createNode():
    return TreeNode()


def insert(root, word):
    currentNode = root

    for c in word:
        if c not in currentNode.children:
            currentNode.children[c] = createNode()
        currentNode = currentNode.children[c]

    currentNode.isEndOfWord = True


def print_tree(node, level=0, prefix="Root: "):
    if node:
        print(" " * (level * 4) + prefix + str(node.isEndOfWord))
        for char, child_node in node.children.items():
            print_tree(child_node, level + 1, f"{char}--- ")


# Test the Tree implementation
if __name__ == "__main__":
    root = createNode()

    # Insert words into the Tree
    insert(root, "apple")
    insert(root, "banana")
    insert(root, "car")
    insert(root, "cat")
    insert(root, "dog")

    print("Tree insertion completed.")

    # Print the Tree structure
    print("Tree Structure:")
    print_tree(root)


import java.util.HashMap;

class TreeNode {
    HashMap children;
    boolean isEndOfWord;

    TreeNode() {
        children = new HashMap<>();
        isEndOfWord = false;
    }
}

public class Tree {
    public static TreeNode createNode() {
        return new TreeNode();
    }

    public static void insert(TreeNode root, String word) {
        TreeNode currentNode = root;

        for (char c : word.toCharArray()) {
            if (!currentNode.children.containsKey(c)) {
                currentNode.children.put(c, createNode());
            }
            currentNode = currentNode.children.get(c);
        }

        currentNode.isEndOfWord = true;
    }

    public static void printTree(TreeNode node, int level, String prefix) {
        if (node != null) {
            System.out.println(" ".repeat(level * 4) + prefix + node.isEndOfWord);
            for (var entry : node.children.entrySet()) {
                printTree(entry.getValue(), level + 1, entry.getKey() + "--- ");
            }
        }
    }

    public static void main(String[] args) {
        TreeNode root = createNode();

        // Insert words into the Tree
        insert(root, "apple");
        insert(root, "banana");
        insert(root, "car");
        insert(root, "cat");
        insert(root, "dog");

        System.out.println("Tree insertion completed.");

        // Print the Tree structure
        System.out.println("Tree Structure:");
        printTree(root, 0, "Root: ");
    }
}


#include 
#include 

class TreeNode {
public:
    std::unordered_map children;
    bool isEndOfWord;

    TreeNode() {
        isEndOfWord = false;
    }
};

TreeNode* createNode() {
    return new TreeNode();
}

void insert(TreeNode* root, const std::string& word) {
    TreeNode* currentNode = root;

    for (char c : word) {
        if (currentNode->children.find(c) == currentNode->children.end()) {
            currentNode->children[c] = createNode();
        }
        currentNode = currentNode->children[c];
    }

    currentNode->isEndOfWord = true;
}

void printTree(TreeNode* node, int level = 0, const std::string& prefix = "Root: ") {
    if (node != nullptr) {
        std::cout << std::string(level * 4, ' ') << prefix << node->isEndOfWord << std::endl;
        for (const auto& entry : node->children) {
            printTree(entry.second, level + 1, entry.first + "--- ");
        }
    }
}

int main() {
    TreeNode* root = createNode();

    // Insert words into the Tree
    insert(root, "apple");
    insert(root, "banana");
    insert(root, "car");
    insert(root, "cat");
    insert(root, "dog");

    std::cout << "Tree insertion completed." << std::endl;

    // Print the Tree structure
    std::cout << "Tree Structure:" << std::endl;
    printTree(root);

    return 0;
}

Output

Tree insertion completed.
Tree Structure:
Root: False
    a--- False
        p--- False
            p--- False
                l--- False
                    e--- True
    b--- False
        a--- False
            n--- False
                a--- False
                    n--- False
                        a--- True
    c--- False
        a--- False
            r--- True
            t--- True
    d--- False
        o--- False
            g--- True

Deletion

Deletion is the removal of a node from the tree. Similar to insertion, the deletion process varies depending on the type of tree and any associated rules or constraints.

Process of deletion in a tree

Start at the root of the tree and initialize a pointer current to the root.
Traverse the tree character by character, following the path of the key to be deleted.
If the current character is not present in the current node's children, the key does not exist in the tree. Return.
If the key still has characters left, move the current pointer to the child node corresponding to the current character and continue to the next character.
If the key has no more characters left, it means we have found the node corresponding to the key.
Mark the node as non-leaf (if it is a leaf node) to indicate that the key no longer exists in the tree.
If the node has no children, i.e., it does not have any other keys associated with it, recursively delete the node.
While deleting the node, move up the tree until you reach a node that has more than one child or is marked as a non-leaf node.
Delete the current node and remove the link from its parent to the current node.
If the node has children, do not delete it. Instead, mark it as non-leaf to indicate that it is no longer associated with the deleted key.


class TreeNode:
    def __init__(self):
        self.children = {}
        self.isEndOfWord = False

def createNode():
    newNode = TreeNode()
    newNode.isEndOfWord = False
    return newNode

def insert(root, word):
    current = root
    for c in word:
        if c not in current.children:
            current.children[c] = createNode()
        current = current.children[c]
    current.isEndOfWord = True

def isEmpty(root):
    return len(root.children) == 0

def remove(root, word, depth=0):
    if root is None:
        return None

    if depth == len(word):
        if root.isEndOfWord:
            root.isEndOfWord = False

            if isEmpty(root):
                del root
                root = None
        return root

    currentChar = word[depth]
    root.children[currentChar] = remove(root.children[currentChar], word, depth + 1)

    if isEmpty(root) and not root.isEndOfWord:
        del root
        root = None

    return root

def printTree(root, prefix):
    if root.isEndOfWord:
        print(prefix)

    for c, child in root.children.items():
        prefix += c
        printTree(child, prefix)
        prefix = prefix[:-1]

if __name__ == '__main__':
    root = createNode()

    insert(root, "apple")
    insert(root, "app")
    insert(root, "application")
    insert(root, "approve")
    insert(root, "bear")

    print("Tree before deletion:")
    prefix = ""
    printTree(root, prefix)
    
    print('\n')
    print("Deleting 'app' from Tree...")
    root = remove(root, "app")
    
    print('\n')
    print("Tree after deletion:")
    prefix = ""
    printTree(root, prefix)


import java.util.HashMap;

class TreeNode {
    HashMap children;
    boolean isEndOfWord;

    TreeNode() {
        children = new HashMap<>();
        isEndOfWord = false;
    }
}

public class Tree {
    public static TreeNode createNode() {
        TreeNode newNode = new TreeNode();
        newNode.isEndOfWord = false;
        return newNode;
    }

    public static void insert(TreeNode root, String word) {
        TreeNode current = root;
        for (char c : word.toCharArray()) {
            if (!current.children.containsKey(c)) {
                current.children.put(c, createNode());
            }
            current = current.children.get(c);
        }
        current.isEndOfWord = true;
    }

    public static boolean isEmpty(TreeNode root) {
        return root.children.isEmpty();
    }

    public static TreeNode remove(TreeNode root, String word, int depth) {
        if (root == null) {
            return null;
        }

        if (depth == word.length()) {
            if (root.isEndOfWord) {
                root.isEndOfWord = false;

                if (isEmpty(root)) {
                    root = null;
                }
            }
            return root;
        }

        char currentChar = word.charAt(depth);
        root.children.put(currentChar, remove(root.children.get(currentChar), word, depth + 1));

        if (isEmpty(root) && !root.isEndOfWord) {
            root = null;
        }

        return root;
    }

    public static void printTree(TreeNode root, StringBuilder prefix) {
        if (root.isEndOfWord) {
            System.out.println(prefix);
        }

        for (HashMap.Entry entry : root.children.entrySet()) {
            prefix.append(entry.getKey());
            printTree(entry.getValue(), prefix);
            prefix.setLength(prefix.length() - 1);
        }
    }

    public static void main(String[] args) {
        TreeNode root = createNode();

        insert(root, "apple");
        insert(root, "app");
        insert(root, "application");
        insert(root, "approve");
        insert(root, "bear");

        System.out.println("Tree before deletion:");
        printTree(root, new StringBuilder());
        
        System.out.println();
        System.out.println("Deleting 'app' from Tree...");
        root = remove(root, "app", 0);
                System.out.println();
                
        System.out.println("Tree after deletion:");
        printTree(root, new StringBuilder());
    }
}


#include <iostream>
#include <unordered_map>

class TreeNode {
public:
    std::unordered_map children;
    bool isEndOfWord;

    TreeNode() {
        isEndOfWord = false;
    }
};

TreeNode* createNode() {
    return new TreeNode();
}

void insert(TreeNode* root, const std::string& word) {
    TreeNode* current = root;
    for (char c : word) {
        if (current->children.find(c) == current->children.end()) {
            current->children[c] = createNode();
        }
        current = current->children[c];
    }
    current->isEndOfWord = true;
}

bool isEmpty(TreeNode* root) {
    return root->children.empty();
}

TreeNode* remove(TreeNode* root, const std::string& word, int depth) {
    if (root == nullptr) {
        return nullptr;
    }

    if (depth == word.length()) {
        if (root->isEndOfWord) {
            root->isEndOfWord = false;

            if (isEmpty(root)) {
                delete root;
                root = nullptr;
            }
        }
        return root;
    }

    char currentChar = word[depth];
    root->children[currentChar] = remove(root->children[currentChar], word, depth + 1);

    if (isEmpty(root) && !root->isEndOfWord) {
        delete root;
        root = nullptr;
    }

    return root;
}

void printTree(TreeNode* root, std::string prefix) {
    if (root->isEndOfWord) {
        std::cout << prefix << std::endl;
    }

    for (const auto& entry : root->children) {
        printTree(entry.second, prefix + entry.first);
    }
}

int main() {
    TreeNode* root = createNode();

    insert(root, "apple");
    insert(root, "app");
    insert(root, "application");
    insert(root, "approve");
    insert(root, "bear");

    std::cout << "Tree before deletion:" << std::endl;
    printTree(root, "");
    
    std::cout << '\n';
    std::cout << "Deleting 'app' from Tree..." << std::endl;
    root = remove(root, "app", 0);
    
        std::cout << '\n';
    std::cout << "Tree after deletion:" << std::endl;
    printTree(root, "");

    return 0;
}

Output

Tree before deletion:
app
apple
application
approve
bear

Deleting 'app' from Tree...

Tree after deletion:
apple
application
approve
bear

Search

Searching in a tree involves finding a specific node or a value within the tree.

Process of search in a tree

Start at the root node of the Tree.
Take the first character of the input string to be searched.
Check if there is a child node in the current node corresponding to the first character.
If there is a child node, move to that child node and proceed to the next character.
If there is no child node, the search string does not exist in the Tree. Return false or an appropriate result.
Repeat step 3 for each subsequent character in the input string.
After traversing all characters of the input string, check if the current node represents the end of a word.
If it does, the search string is found in the Tree. Return true or an appropriate result.
If it doesn't, the search string is a prefix of another word in the Tree, but not a complete word. Return false or an appropriate result.


class TreeNode:
    def __init__(self):
        self.children = {}
        self.isWord = False

class Tree:
    def __init__(self):
        self.root = TreeNode()

    def insert(self, word):
        node = self.root
        for ch in word:
            if ch not in node.children:
                node.children[ch] = TreeNode()
            node = node.children[ch]
        node.isWord = True

    def search(self, word):
        node = self.root
        for ch in word:
            if ch not in node.children:
                return False
            node = node.children[ch]
        return node.isWord


tree = Tree()
tree.insert("apple")
tree.insert("banana")
tree.insert("orange")
tree.insert("pear")

print("Search results:")
print("apple:", "Found" if tree.search("apple") else "Not found")
print("banana:", "Found" if tree.search("banana") else "Not found")
print("orange:", "Found" if tree.search("orange") else "Not found")
print("pear:", "Found" if tree.search("pear") else "Not found")
print("grapes:", "Found" if tree.search("grape") else "Not found")


import java.util.HashMap;
import java.util.Map;

class TreeNode {
    Map children;
    boolean isWord;

    public TreeNode() {
        this.children = new HashMap<>();
        this.isWord = false;
    }
}

class Tree {
    TreeNode root;

    public Tree() {
        this.root = new TreeNode();
    }

    public void insert(String word) {
        TreeNode node = root;
        for (char ch : word.toCharArray()) {
            if (!node.children.containsKey(ch)) {
                node.children.put(ch, new TreeNode());
            }
            node = node.children.get(ch);
        }
        node.isWord = true;
    }

    public boolean search(String word) {
        TreeNode node = root;
        for (char ch : word.toCharArray()) {
            if (!node.children.containsKey(ch)) {
                return false;
            }
            node = node.children.get(ch);
        }
        return node.isWord;
    }
}

public class Main {
    public static void main(String[] args) {
        Tree tree = new Tree();
        tree.insert("apple");
        tree.insert("banana");
        tree.insert("orange");
        tree.insert("pear");

        System.out.println("Search results:");
        System.out.println("apple: " + (tree.search("apple") ? "Found" : "Not found"));
        System.out.println("banana: " + (tree.search("banana") ? "Found" : "Not found"));
        System.out.println("orange: " + (tree.search("orange") ? "Found" : "Not found"));
        System.out.println("pear: " + (tree.search("pear") ? "Found" : "Not found"));
        System.out.println("grapes: " + (tree.search("grape") ? "Found" : "Not found"));
    }
}


#include 
#include 

class TreeNode {
public:
    std::unordered_map children;
    bool isWord;

    TreeNode() : isWord(false) {}
};

class Tree {
public:
    TreeNode* root;

    Tree() : root(new TreeNode()) {}

    void insert(const std::string& word) {
        TreeNode* node = root;
        for (char ch : word) {
            if (node->children.find(ch) == node->children.end()) {
                node->children[ch] = new TreeNode();
            }
            node = node->children[ch];
        }
        node->isWord = true;
    }

    bool search(const std::string& word) {
        TreeNode* node = root;
        for (char ch : word) {
            if (node->children.find(ch) == node->children.end()) {
                return false;
            }
            node = node->children[ch];
        }
        return node->isWord;
    }
};

int main() {
    Tree tree;
    tree.insert("apple");
    tree.insert("banana");
    tree.insert("orange");
    tree.insert("pear");

    std::cout << "Search results:" << std::endl;
    std::cout << "apple: " << (tree.search("apple") ? "Found" : "Not found") << std::endl;
    std::cout << "banana: " << (tree.search("banana") ? "Found" : "Not found") << std::endl;
    std::cout << "orange: " << (tree.search("orange") ? "Found" : "Not found") << std::endl;
    std::cout << "pear: " << (tree.search("pear") ? "Found" : "Not found") << std::endl;
    std::cout << "grapes: " << (tree.search("grape") ? "Found" : "Not found") << std::endl;

    return 0;
}

Output

 Search results:
apple: Found
banana: Found
orange: Found
pear: Found
grapes: Not found

Applications of Tree Data Structure

Binary Search Trees(BSTs) are used to quickly check whether an element is present in a set or not.
A heap is a kind of tree that is used for heap sort.
A modified version of a tree called Tries is used in modern routers to store routing information.
Most popular databases use B-trees and T-trees, which are variants of the tree structure to store their data.
Compilers use a syntax tree to validate the syntax of every program you write.
Huffman coding is a popular technique for data compression that involves constructing a binary tree where the leaves represent characters and their frequency of occurrence. The resulting tree is used to encode the data in a way that minimizes the amount of storage required.

Summary

In this tutorial, we have learned all about Trees in data structures, terminologies, basic operations, and applications of trees. Trees are a robust data structure that can help solve complex problems efficiently. They offer many advantages, such as the ability to search quickly and sort, store objects in an organized manner, and provide flexibility when dealing with complicated data sets. To test your knowledge of trees, enroll in our DSA Programming Course.

FAQs

It is th length of the longest path from the root of the tree to a leaf node of the tree.

Every tree is a combination of

A node carrying data
Two subtrees

01 Career Opportunities

02 Beginner

03 Intermediate

04 Advanced

05 Questions

06 Training Programs

Trees in Data Structures - Its Structure, Operations & Applications

Trees in Data Structures: An Overview

What is a Tree Data Structure?

Terminologies in Tree Data Structure

Representation of a Tree in Data Structures

How to declare/create a Tree in Data Structures?

Types Of Trees in Data Structures

Standard Operations on Trees in Data Structures

Traversal

Example of Tree Traversal in Tree Data Structure

Output

Insertion

Output

Deletion

Output

Search

Output

Applications of Tree Data Structure

Summary

FAQs

About Author

Live Batches Schedule View All

01 Career Opportunities

02 Beginner

03 Intermediate

04 Advanced

05 Questions

06 Training Programs

Trees in Data Structures - Its Structure, Operations & Applications

Trees in Data Structures: An Overview

What is a Tree Data Structure?

Terminologies in Tree Data Structure

Representation of a Tree in Data Structures

How to declare/create a Tree in Data Structures?

Types Of Trees in Data Structures

Standard Operations on Trees in Data Structures

Traversal

Example of Tree Traversal in Tree Data Structure

Output

Insertion

Output

Deletion

Output

Search

Output

Applications of Tree Data Structure

Summary

FAQs

Q1. What is the height of a Tree in Data Structures?

Q2. What a tree in data structures consists of?

Q3. What are the types Of Trees in Data Structures?

About Author

Live Batches Schedule View All