Radix Sort in Data Structures - Its Algorithm, Working, & Complexity

Radix Sort in Data Structures: An Overview

We have seen that we can sort an array based on the frequency of elements using the Counting Sort. However, we learned that it is not efficient if the range of elements is very large. To overcome this limitation, we have with us the radix sort algorithm. In this DSA tutorial, we will learn its features, working, implementation, etc.

To further enhance your understanding and application of radix sort, consider enrolling in the Best Dsa Course to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Radix Sort in Data Structures?

Radix Sort is a linear non-comparative sorting algorithm that sorts elements by processing them digit by digit. It applies counting sort digit by digit from least-significant digit to most-significant digit on the given array. It first groups the individual digits of the same place value. Afterward, it sorts the elements according to their increasing/decreasing order.

Before moving forward, if you haven't come across Counting Sort in Data Structures, please refer to it and come back. It's an important prerequisite for learning radix sort because counting sort is used as an intermediate sort in radix sort.

Radix Sort Algorithm

radixSort(array)
  d <- maximum number of digits in the largest element
  create d buckets of size 0-9
  for i <- 0 to d
    sort the elements according to ith place digits using countingSort

countingSort(array, d)
  max <- find largest element among dth place elements
  initialize count array with all zeros
  for j <- 0 to size
    find the total count of each unique digit in dth place of elements and
    store the count at jth index in count array
  for i <- 1 to max
    find the cumulative sum and store it in count array itself
  for j <- size down to 1
    restore the elements to array
    decrease count of each element restored by 1

Working of the Radix Sort Algorithm

1. Find the largest element in the array, i.e. max. Let X be the number of digits in max. X is calculated because we have to go through all the significant places of all elements.

   

   In the given array, the largest number is 801. It has 3 digits. Therefore, the loop should go up to the hundreds place(3 times).
2. Now, go through each significant place one by one.

   Use any stable sorting technique to sort the digits at each significant place. We will use counting sort for this.

   Sort the elements based on the unit place digits (X=0).

   

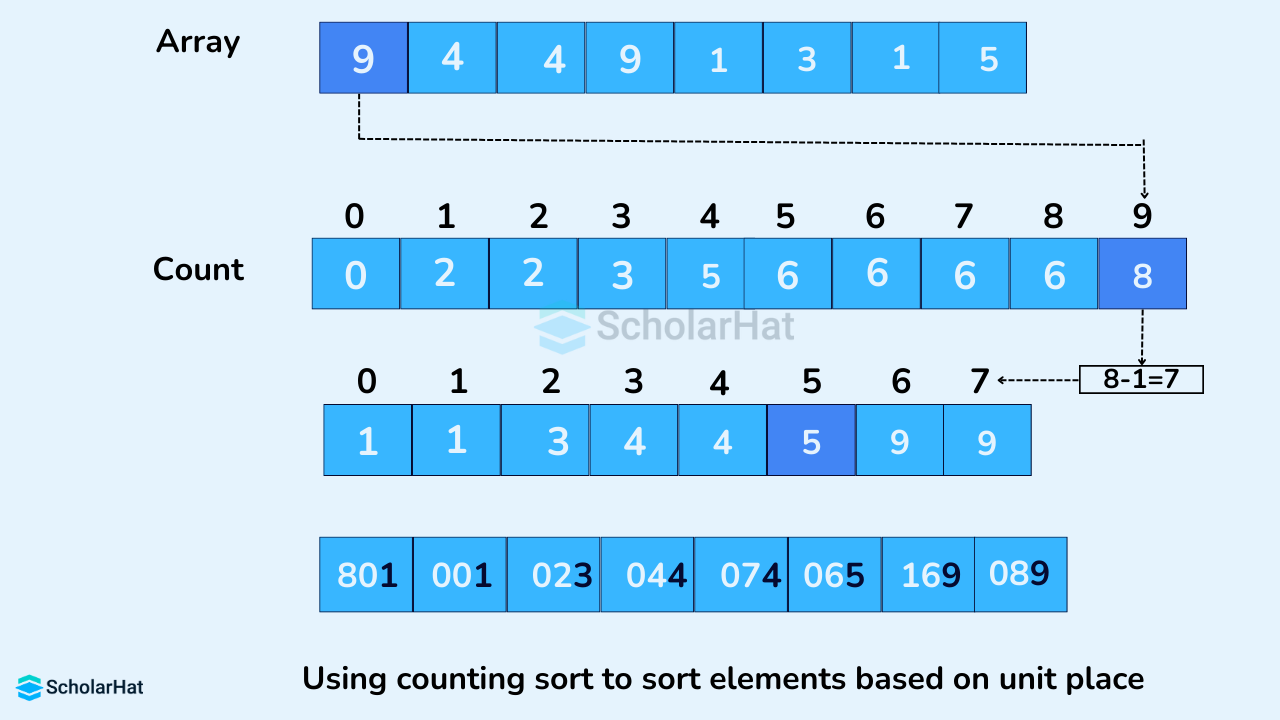
3. Now, sort the elements based on digits at the tens place.

   

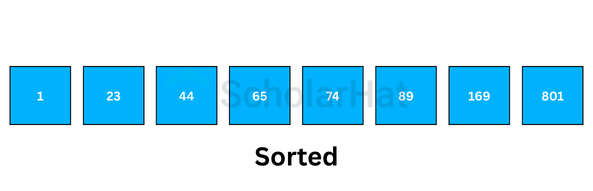
4. Finally, sort the elements based on the digits at hundreds place.

The final sorted array will be:

Read More - Data Structure Interview Questions and Answers

Implementation of Radix Sort in Different Languages in Data Structures

# Using counting sort to sort the elements in the basis of significant places
def countingSort(array, place):
    size = len(array)
    output = [0] * size
    count = [0] * 10

    # Calculate count of elements
    for i in range(0, size):
        index = array[i] // place
        count[index % 10] += 1

    # Calculate cumulative count
    for i in range(1, 10):
        count[i] += count[i - 1]

    # Place the elements in sorted order
    i = size - 1
    while i >= 0:
        index = array[i] // place
        output[count[index % 10] - 1] = array[i]
        count[index % 10] -= 1
        i -= 1

    for i in range(0, size):
        array[i] = output[i]


# Main function to implement radix sort
def radixSort(array):
    # Get the maximum element
    max_element = max(array)

    # Apply counting sort to sort elements based on place value.
    place = 1
    while max_element // place > 0:
        countingSort(array, place)
        place *= 10

def print_list(arr):
    for i in range(len(arr)):
        print(arr[i], end=" ")
    print()

arr = [169, 44, 74, 89, 801, 23, 1, 65]
print("Original array is:", end=" ")
print_list(arr)

radixSort(arr)

print("Sorted Array in Ascending Order:", end=" ")
print_list(arr)

import java.util.Arrays;

public class RadixSort {
    static void countingSort(int[] array, int place) {
        int size = array.length;
        int[] output = new int[size];
        int[] count = new int[10];

        // Calculate count of elements
        for (int i = 0; i < size; i++) {
            int index = array[i] / place;
            count[index % 10]++;
        }

        // Calculate cumulative count
        for (int i = 1; i < 10; i++) {
            count[i] += count[i - 1];
        }

        // Place the elements in sorted order
        for (int i = size - 1; i >= 0; i--) {
            int index = array[i] / place;
            output[count[index % 10] - 1] = array[i];
            count[index % 10]--;
        }

        System.arraycopy(output, 0, array, 0, size);
    }

    static void radixSort(int[] array) {
        int max_element = Arrays.stream(array).max().getAsInt();
        int place = 1;
        while (max_element / place > 0) {
            countingSort(array, place);
            place *= 10;
        }
    }

    static void printArray(int[] arr) {
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] arr = {169, 44, 74, 89, 801, 23, 1, 65};
        System.out.print("Original array is: ");
        printArray(arr);

        radixSort(arr);

        System.out.print("Sorted Array in Ascending Order: ");
        printArray(arr);
    }
}
    

#include 
using namespace std;

// Function to get the largest element from an array
int getMax(int array[], int n) {
  int max = array[0];
  for (int i = 1; i < n; i++)
    if (array[i] > max)
      max = array[i];
  return max;
}

// Using counting sort to sort the elements in the basis of significant places
void countingSort(int array[], int size, int place) {
  const int max = 10;
  int output[size];
  int count[max];

  for (int i = 0; i < max; ++i)
    count[i] = 0;

  // Calculate count of elements
  for (int i = 0; i < size; i++)
    count[(array[i] / place) % 10]++;

  // Calculate cumulative count
  for (int i = 1; i < max; i++)
    count[i] += count[i - 1];

  // Place the elements in sorted order
  for (int i = size - 1; i >= 0; i--) {
    output[count[(array[i] / place) % 10] - 1] = array[i];
    count[(array[i] / place) % 10]--;
  }

  for (int i = 0; i < size; i++)
    array[i] = output[i];
}

// Main function to implement radix sort
void radixsort(int array[], int size) {
  // Get maximum element
  int max = getMax(array, size);

  // Apply counting sort to sort elements based on place value.
  for (int place = 1; max / place > 0; place *= 10)
    countingSort(array, size, place);
}

// Print an array
void printArray(int array[], int size) {
  int i;
  for (i = 0; i < size; i++)
    cout << array[i] << " ";
  cout << endl;
}

int main() {
  int array[] = {169, 44, 74, 89, 801, 23, 1, 65};
  int n = sizeof(array) / sizeof(array[0]);
  cout << "Original array is: ";
  printArray(array, n);
  
  radixsort(array, n);
  
  cout << "Sorted Array in Ascending Order: ";
  printArray(array, n);
  return 0;
}
    

Output

Original array is: 169 44 74 89 801 23 1 65 
Sorted Array in Ascending Order: 1 23 44 65 74 89 169 801 

Complexity Analysis of Radix Sort Algorithm

1. Time Complexity

   Case	Time Complexity
   Best	O(n+k)
   Average	O(n+k)
   Worst	O(n+k)

   If radix sort uses counting sort as an intermediate stable sort, the time complexity is O(d(n+k)). Here, d is the number cycle and O(n+k) is the time complexity of counting sort.

2. Space Complexity: The space complexity of the radix sort algorithm is O(max).

Applications of the Radix Sort Algorithm

1. Integer Sorting: Radix sort can efficiently sort integers of fixed size. For example, if you have a large collection of 32-bit integers, the radix sort can sort them in linear time by considering each digit's position.
2. String Sorting: Radix sort can be used to sort strings of fixed length or strings with a common maximum length. By considering each character's position, radix sort can order strings based on their character values.
3. IP Address Sorting: Radix sort is often used to sort IP addresses in network applications. IP addresses can be represented as a sequence of numbers separated by periods (e.g., 192.168.0.1). Radix sort can sort IP addresses by considering each octet (digit between periods) from left to right.
4. Phone Number Sorting: In certain applications, you may need to sort phone numbers based on their numerical value. Radix sort can be used to sort phone numbers by considering each digit's position, providing a fast and efficient sorting method.
5. Data Radix Transformation: Radix sort can also be used as a preprocessing step to transform data into a different Radix representation. For example, it can convert numbers from decimal to binary or hexadecimal representation.

Advantages of the Radix Sort Algorithm

1. Efficient for large data sets: Radix sort has a linear time complexity. This makes it efficient for sorting large data sets, especially when the number of elements is significantly larger than the average length of the elements.
2. Stable sorting: Radix sort is a stable sorting algorithm, which means that elements with equal keys maintain their relative order after sorting.
3. Suitable for fixed-length keys: Radix sort is particularly effective when sorting elements with fixed-length keys. It can process each digit or character position independently, making it well-suited for sorting strings, integers, or other data types with a fixed number of digits or characters.
4. No dependency on comparison operations: Unlike comparison-based sorting algorithms like quick sort or merge sort, radix sort does not rely on comparison operations between elements.

Disadvantages of the Radix Sort Algorithm

1. Limited Applicability: Radix sort is primarily suitable for sorting fixed-size integers or strings with a consistent length. It becomes less efficient when dealing with variable-length inputs.
2. Space Complexity: Radix sort requires additional space to store intermediate results during sorting. The amount of space required depends on the range of values being sorted. In some cases, this can lead to increased memory usage, especially when sorting large datasets.
3. Inefficient for small data sets: It is not efficient for small data sets or data sets with a small number of unique keys.

Summary

So, here we saw every aspect of the radix sort algorithm in data structures. I know it's quite difficult and tricky to understand the whole topic in a single go. It will be difficult if you aren't well-versed with the counting sort algorithm. To apply your knowledge of the radix sort algorithm, enroll in our Dsa Training.

Similar Sorting Algorithms

• Counting Sort
• Merge Sort
• Quick Sort
• Bucket Sort