26
DecQueue in Data Structures - Types & Algorithm (With Example)
In this DSA tutorial, you will examine queue in data structure, characteristics of queue in data structure, basic operations of queue in data structure, its working, different types of queues in data structures, including simple queues, circular queues, and priority queues. etc., further you will enhance your understanding on application of queue concepts, advantages and disadvantages of queue in data structure. 90% of coding interviews focus on DSA – Get ahead with our Free DSA Course, earn a career-boosting certificate. Let's dive in!
What is a Queue in Data Structures?
Queue is a widely used linear, non-primitive data structure that models real-world scenarios where data must be processed in the same order in which it arrives. A queue is an ordered list in which insertion is done at one end called REAR and deletion at another end called FRONT.
The first inserted element is available first for the operations to be performed and is the first one to be deleted. Hence, it is known as First In First Out, FIFO or Last In Last Out, LILO.
Queues are particularly useful in situations where data must be stored temporarily and processed sequentially. This includes operating systems (job scheduling, disk scheduling, interrupt handling), breadth-first search (BFS) in graphs, data streaming, and network packet management.
Real Life Example:
- A ticket queue outside a ticket counter,
- Students standing in a queue for assembly prayer on the school grounds,
- And a queue of persons standing outside the booking counter of a theatre.
In all these examples, the person standing first in the line is the first one for access, which follows First in First Out (FIFO principle).
Working of Queue in Data Structures
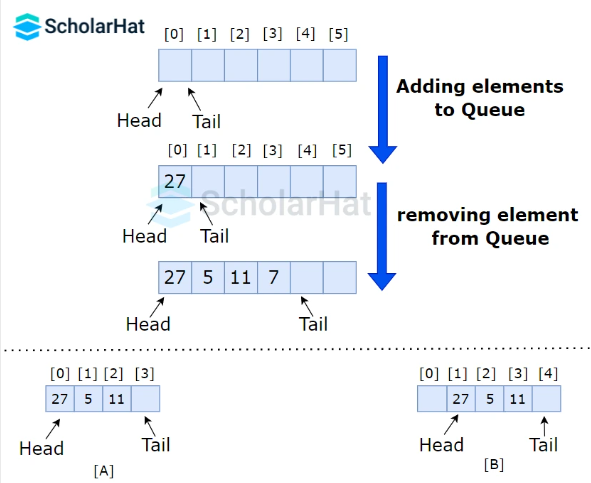
Queue operations work as follows:
- Two pointers are there denoting two ends, FRONT and REAR.
- FRONT Tracks the first element of the queue.
- REAR Tracks the last element of the queue.
- Initially, set the value of FRONT and REAR to -1.
- Afterward, follow the above-given algorithms for the basic operations.
Key Characteristics of Queue
1. FIFO Principle (First-In, First-Out)
- The element inserted first is removed first.
- Example: Like a line of people waiting—first person to enter the line is the first to be served.
2. Two Main Pointers: We know that a queue can be accessed from both sides.
- Front: Position of the entry in a queue ready to be served, that is, the first entry that will be removed from the queue, is called the front of the queue. It is also referred as the head of the queue.
- Rear: Position of the last entry in the queue, that is, the one most recently added, is called the rear of the queue. It is also referred as the tail of the queue.
3. Basic Operations
- enqueue(): Insert an element at the rear.
- dequeue(): Remove an element from the front.
- peek(): View the front element without removing it.
- isEmpty(): Check if the queue has no elements.
- isFull(): (for fixed-size queues) Checks if the queue is full.
4. Linear Structure
- Elements are stored and accessed in a sequential manner.
5. Dynamic or Static Implementation
- Can be implemented using: Arrays (static, with fixed size), Linked Lists (dynamic, resizable), Circular arrays (efficient memory reuse)
| Read More - Differences Between Stack and Queue Data Structures |
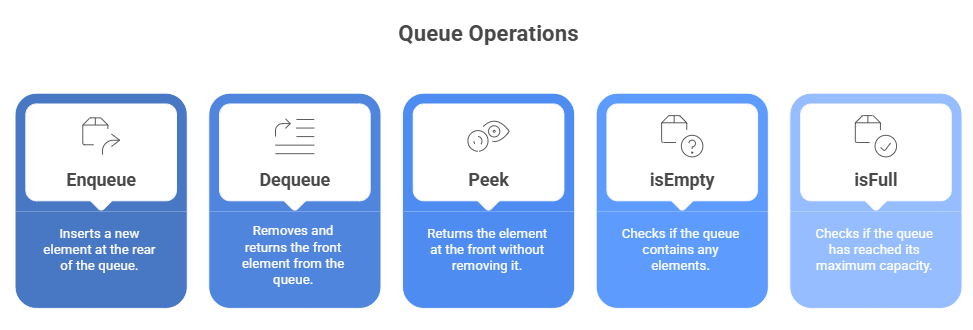
Basic Operations of Queue in Data Structures
Let's see the basic operations in Queue:
- Enqueue – Adds an element to the rear of the queue.
- Dequeue – Removes and returns the front element.
- Peek/Front – Returns the front element without removing it.
- isEmpty – Checks if the queue is empty.
- isFull – Checks if the queue is full (for fixed-size queues).
- Insertion: enqueue()
The enqueue() The operation inserts an element from the back of a queue to the end of a queue or the rear end of the queue.
Algorithm
Step 1: START
Step 2: Check if the queue is full.
Step 3: If the queue is full, produce an overflow error and exit.
Step 4: If the queue is not full, increment the rear pointer to point to the next space.
Step 5: Add a data element to the queue location, where the rear is pointing.
Step 6: End the process and exit.
- Deletion: dequeue()
The dequeue() Operation is used to remove and return the element from the front of a queue.
Algorithm
Step 1: START
Step 2: Check if the queue is empty.
Step 3: If the queue is empty, print underflow and exit.
Step 4: If the queue is not empty, access the data where the front is pointing.
Step 5: Increment the front pointer to point to the next available data element.
Step 6: Set the front and rear as -1 for the last element.
Step 7: End the process and exit.
- peek()
The peek()The operation returns the value at the front end of the queue without removing it.
Algorithm
Step 1: START
Step 2: Check if the Queue is empty.
Step 3: Return the element at the front of the queue
Step 4: End the process and exit.
- isFull()
The isFull() operation is used to determine if the queue is full or not. A queue is said to be full if it has reached its maximum capacity and there is no more space to add new elements to it.
Algorithm
Step 1: START
Step 2: If the count of queue elements equals the queue size, return true.
Step 3: Otherwise, return false
Step 4: End the process and exit.
- isEmpty()
The isEmpty() operation is used to check if the queue is empty or not. It returns a boolean value, true when the queue is empty, otherwise false.
Algorithm
Step 1: START
Step 2: If the count of queue elements equals zero, return true.
Step 3: Otherwise, return false
Step 4: End the process and exit.
Read More - DSA Interview Questions and Answers
Complexity Analysis of Operations on Queue
| Operation | Time Complexity | Space Complexity | Explanation |
| enqueue(x) | O(1) | O(1) | Adds an element at the rear. Constant time. |
| dequeue() | O(1) | O(1) | Removes element from the front. Constant time. |
| peek() | O(1) | O(1) | Accesses the front element without removal. |
| isEmpty() | O(1) | O(1) | Checks whether the queue has no elements. |
| isFull() | O(1) | O(1) | (For fixed-size queues like arrays or circular queue) |
Types of Queues in Data Structures
There are 4 types of queues in data structures:
1. Simple or Linear Queue
- As we mentioned above, a Simple queue follows the First-In-First-Out (FIFO) principle.
- In this, Items are taken out of the front and put in the back.
- It is necessary to remove outdated elements in order to add new ones.
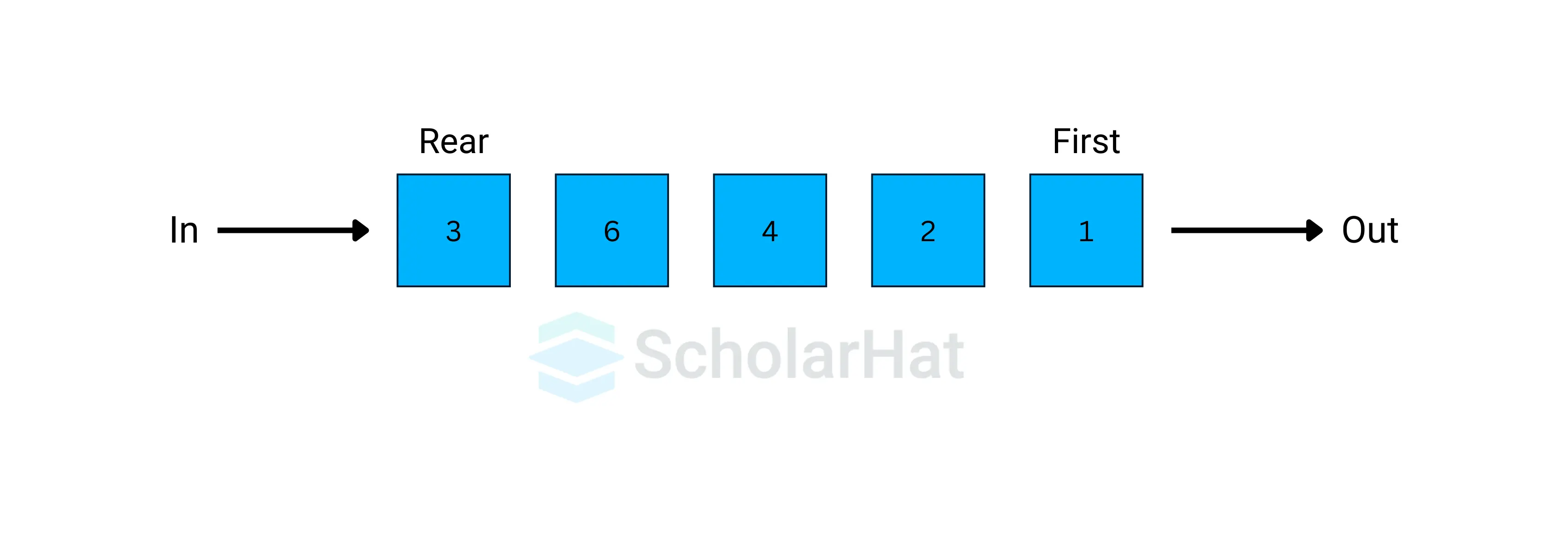
2. Circular Queue
- A circular queue is similar to a simple queue, but the last element is connected to the first element which creates a circular structure.
- This allows for efficient use of memory.
- It is also known as a Ring Buffer.
| Circular Queue in Data Structures |
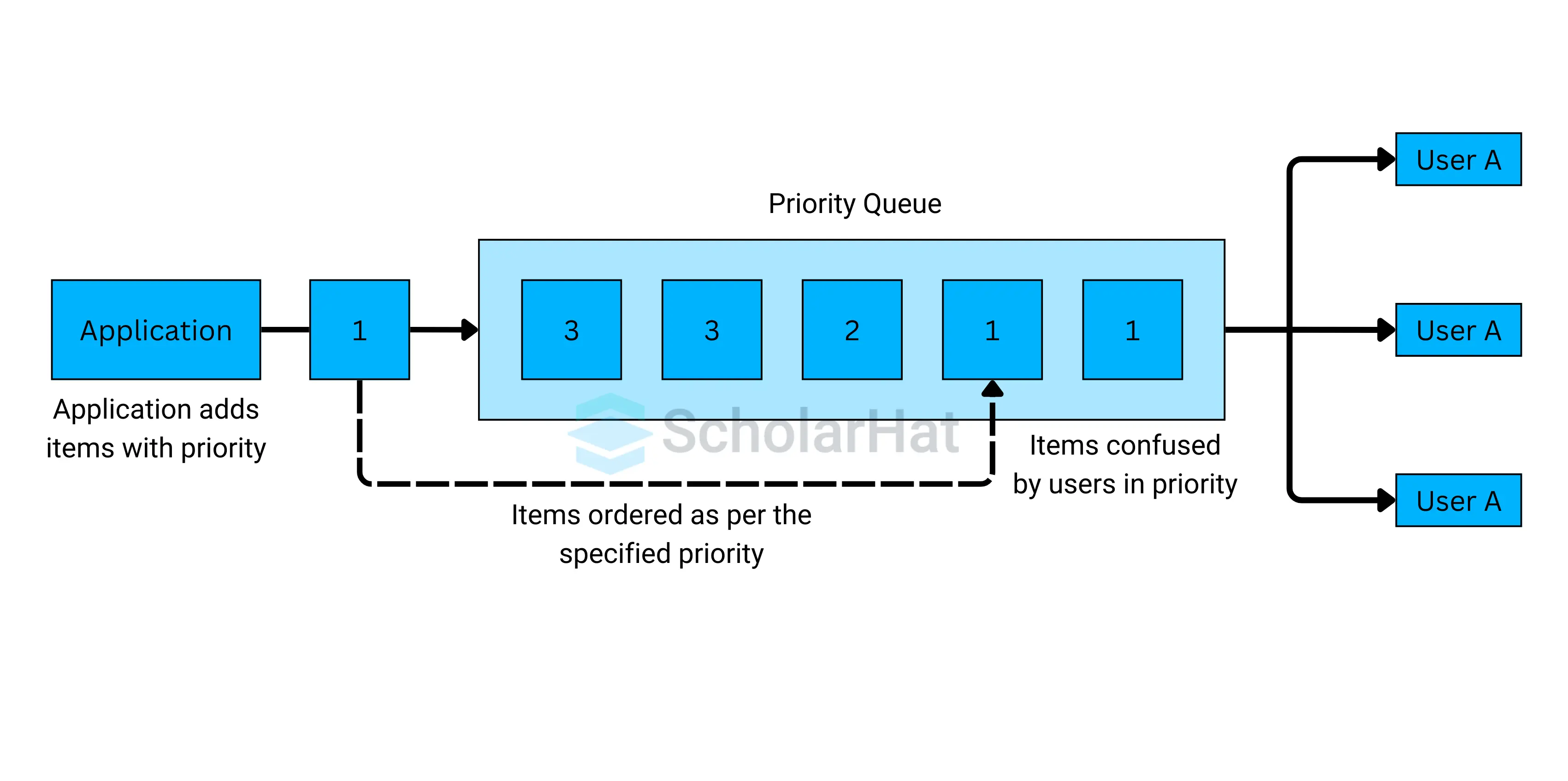
3. Priority Queue in Data Structure
- It is a special type of queue in which each element has a priority assigned to it.
- The element with the highest priority is removed first.
- This is useful in situations where certain elements need to be processed before others.
They are of two types :
- Ascending Priority Queue: Elements are ordered by increasing priority value. Element with smallest priority value is popped first.
- Descending Priority Queue: Elements are ordered by increasing priority value. Element with largest priority is popped first.
4. Dequeue (Double-Ended Queue)
- In this, the elements can be added or removed from both ends
frontandrearof the queue. - It provides flexibility in managing data with operations from both ends.
They are of two types:
- Input Restricted Queue: This is a simple queue. In this type of queue, the input can be taken from only one end but deletion can be done from any of the ends.
- Output Restricted Queue: This is also a simple queue. In this type of queue, the input can be taken from both ends but deletion can be done from only one end.

Implementation of Queue in Different Programming Languages
There are three ways to implement Queues in Data Structures, using a 1D Array, a Single Linked List, and vectors. We will look at array and linked list implementation in detail.
- Implementation of Queue Using a 1D Array
It is the simplest implementation of a Queue in Data Structures. We usually use arrays to implement queues in Java and C++. In the case of Python, we use lists.
The time complexity of all the operations is the same i.e. O(1) here.
#include <stdio.h>
#include <stdlib.h>
#include<limits.h>
// Define the Queue structure
typedef struct Queue {
int front, rear, size;
unsigned capacity;
int* array;
} Queue;
// Function to create a queue of given capacity.
// It initializes size of queue as 0
Queue* createQueue(unsigned capacity) {
Queue* queue = (Queue*)malloc(sizeof(Queue));
queue->capacity = capacity;
queue->front = queue->size = 0;
queue->rear = capacity - 1;
queue->array = (int*)malloc(queue->capacity * sizeof(int));
return queue;
}
// Queue is full when size becomes equal to the capacity
int isFull(Queue* queue) {
return (queue->size == queue->capacity);
}
// Queue is empty when size is 0
int isEmpty(Queue* queue) {
return (queue->size == 0);
}
// Function to add an item to the queue.
// It changes rear and size
void enqueue(Queue* queue, int item) {
if (isFull(queue)) {
return;
}
queue->rear = (queue->rear + 1) % queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
printf("%d enqueued to queue\n", item);
}
// Function to remove an item from queue.
// It changes front and size
int dequeue(Queue* queue) {
if (isEmpty(queue)) {
return INT_MIN;
}
int item = queue->array[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
queue->size = queue->size - 1;
return item;
}
// Function to get front of queue
int getFront(Queue* queue) {
if (isEmpty(queue)) {
return INT_MIN;
}
return queue->array[queue->front];
}
// Function to get rear of queue
int getRear(Queue* queue) {
if (isEmpty(queue)) {
return INT_MIN;
}
return queue->array[queue->rear];
}
// Main function to test the above functions
int main() {
// Create a queue with a capacity of 100
Queue* queue = createQueue(100);
// Enqueue elements into the queue
enqueue(queue, 10);
enqueue(queue, 15);
enqueue(queue, 20);
enqueue(queue, 25);
enqueue(queue, 30);
// Dequeue elements from the queue
printf("%d dequeued from queue\n", dequeue(queue));
printf("%d dequeued from queue\n", dequeue(queue));
printf("%d dequeued from queue\n", dequeue(queue));
// Display the front and rear elements of the queue
printf("Front item is %d\n", getFront(queue));
printf("Rear item is %d\n", getRear(queue));
// Free allocated memory
free(queue->array);
free(queue);
return 0;
}
#include<iostream>
#include<climits>
using namespace std;
class Queue {
int front, rear, size;
unsigned capacity;
int* array;
public:
Queue(unsigned capacity);
~Queue();
bool isFull();
bool isEmpty();
void enqueue(int item);
int dequeue();
int getFront();
int getRear();
};
Queue::Queue(unsigned capacity) {
this->capacity = capacity;
this->front = this->size = 0;
this->rear = capacity - 1;
this->array = new int[capacity];
}
Queue::~Queue() {
delete[] array;
}
bool Queue::isFull() {
return (this->size == this->capacity);
}
bool Queue::isEmpty() {
return (this->size == 0);
}
void Queue::enqueue(int item) {
if (isFull())
return;
this->rear = (this->rear + 1) % this->capacity;
this->array[this->rear] = item;
this->size = this->size + 1;
cout << item << " enqueued to queue\n";
}
int Queue::dequeue() {
if (isEmpty())
return INT_MIN;
int item = this->array[this->front];
this->front = (this->front + 1) % this->capacity;
this->size = this->size - 1;
return item;
}
int Queue::getFront() {
if (isEmpty())
return INT_MIN;
return this->array[this->front];
}
int Queue::getRear() {
if (isEmpty())
return INT_MIN;
return this->array[this->rear];
}
int main() {
// Create a queue with a capacity of 100
Queue queue(100);
// Enqueue elements into the queue
queue.enqueue(10);
queue.enqueue(15);
queue.enqueue(20);
queue.enqueue(25);
queue.enqueue(30);
// Dequeue elements from the queue
cout << queue.dequeue() << " dequeued from queue\n";
cout << queue.dequeue() << " dequeued from queue\n";
cout << queue.dequeue() << " dequeued from queue\n";
// Display the front and rear elements of the queue
cout << "Front item is " << queue.getFront() << endl;
cout << "Rear item is " << queue.getRear() << endl;
return 0;
}
using System;
public class Queue
{
private int capacity;
private int front;
private int size;
private int rear;
private int[] array;
public Queue(int capacity)
{
this.capacity = capacity;
this.front = this.size = 0;
this.rear = capacity - 1;
this.array = new int[this.capacity];
}
public bool IsFull()
{
return this.size == this.capacity;
}
public bool IsEmpty()
{
return this.size == 0;
}
public void Enqueue(int item)
{
if (this.IsFull())
return;
this.rear = (this.rear + 1) % this.capacity;
this.array[this.rear] = item;
this.size++;
Console.WriteLine($"{item} enqueued to queue");
}
public int Dequeue()
{
if (this.IsEmpty())
return int.MinValue;
int item = this.array[this.front];
this.front = (this.front + 1) % this.capacity;
this.size--;
return item;
}
public int GetFront()
{
return this.IsEmpty() ? int.MinValue : this.array[this.front];
}
public int GetRear()
{
return this.IsEmpty() ? int.MinValue : this.array[this.rear];
}
public static void Main(string[] args)
{
Queue queue = new Queue(100);
queue.Enqueue(10);
queue.Enqueue(15);
queue.Enqueue(20);
queue.Enqueue(25);
queue.Enqueue(30);
Console.WriteLine($"{queue.Dequeue()} dequeued from queue");
Console.WriteLine($"{queue.Dequeue()} dequeued from queue");
Console.WriteLine($"{queue.Dequeue()} dequeued from queue");
Console.WriteLine("Front item is " + queue.GetFront());
Console.WriteLine("Rear item is " + queue.GetRear());
}
}
class Queue:
def __init__(self, capacity):
self.capacity = capacity
self.front = self.size = 0
self.rear = capacity - 1
self.array = [0] * self.capacity
def is_full(self):
return self.size == self.capacity
def is_empty(self):
return self.size == 0
def enqueue(self, item):
if self.is_full():
return
self.rear = (self.rear + 1) % self.capacity
self.array[self.rear] = item
self.size += 1
print(f"{item} enqueued to queue")
def dequeue(self):
if self.is_empty():
return float('-inf')
item = self.array[self.front]
self.front = (self.front + 1) % self.capacity
self.size -= 1
return item
def get_front(self):
return self.array[self.front] if not self.is_empty() else float('-inf')
def get_rear(self):
return self.array[self.rear] if not self.is_empty() else float('-inf')
if __name__ == "__main__":
# Create a queue with a capacity of 100
queue = Queue(100)
# Enqueue elements into the queue
queue.enqueue(10)
queue.enqueue(15)
queue.enqueue(20)
queue.enqueue(25)
queue.enqueue(30)
# Dequeue elements from the queue
print(f"{queue.dequeue()} dequeued from queue")
print(f"{queue.dequeue()} dequeued from queue")
print(f"{queue.dequeue()} dequeued from queue")
# Display the front and rear elements of the queue
print("Front item is", queue.get_front())
print("Rear item is", queue.get_rear())
public class Queue {
int front, rear, size;
int capacity;
int[] array;
// Function to create a queue of given capacity
public Queue(int capacity) {
this.capacity = capacity;
this.front = this.size = 0;
this.rear = capacity - 1;
this.array = new int[this.capacity];
}
// Function to check if the queue is full
boolean isFull() {
return (this.size == this.capacity);
}
// Function to check if the queue is empty
boolean isEmpty() {
return (this.size == 0);
}
// Function to enqueue an item
void enqueue(int item) {
if (isFull())
return;
this.rear = (this.rear + 1) % this.capacity;
this.array[this.rear] = item;
this.size = this.size + 1;
System.out.println(item + " enqueued to queue");
}
// Function to dequeue an item
int dequeue() {
if (isEmpty())
return Integer.MIN_VALUE;
int item = this.array[this.front];
this.front = (this.front + 1) % this.capacity;
this.size = this.size - 1;
return item;
}
// Function to get the front item of the queue
int front() {
if (isEmpty())
return Integer.MIN_VALUE;
return this.array[this.front];
}
// Function to get the rear item of the queue
int rear() {
if (isEmpty())
return Integer.MIN_VALUE;
return this.array[this.rear];
}
public static void main(String[] args) {
// Create a queue with a capacity of 100
Queue queue = new Queue(100);
// Enqueue elements into the queue
queue.enqueue(10);
queue.enqueue(15);
queue.enqueue(20);
queue.enqueue(25);
queue.enqueue(30);
// Dequeue elements from the queue
System.out.println(queue.dequeue() + " dequeued from queue");
System.out.println(queue.dequeue() + " dequeued from queue");
System.out.println(queue.dequeue() + " dequeued from queue");
// Display the front and rear elements of the queue
System.out.println("Front item is " + queue.front());
System.out.println("Rear item is " + queue.rear());
}
}
class Queue {
constructor(capacity) {
this.capacity = capacity;
this.front = this.size = 0;
this.rear = capacity - 1;
this.array = new Array(this.capacity).fill(0);
}
isFull() {
return this.size === this.capacity;
}
isEmpty() {
return this.size === 0;
}
enqueue(item) {
if (this.isFull()) return;
this.rear = (this.rear + 1) % this.capacity;
this.array[this.rear] = item;
this.size++;
console.log(`${item} enqueued to queue`);
}
dequeue() {
if (this.isEmpty()) return Number.NEGATIVE_INFINITY;
const item = this.array[this.front];
this.front = (this.front + 1) % this.capacity;
this.size--;
return item;
}
getFront() {
return this.isEmpty() ? Number.NEGATIVE_INFINITY : this.array[this.front];
}
getRear() {
return this.isEmpty() ? Number.NEGATIVE_INFINITY : this.array[this.rear];
}
}
// Create a queue with a capacity of 100
const queue = new Queue(100);
// Enqueue elements into the queue
queue.enqueue(10);
queue.enqueue(15);
queue.enqueue(20);
queue.enqueue(25);
queue.enqueue(30);
// Dequeue elements from the queue
console.log(`${queue.dequeue()} dequeued from queue`);
console.log(`${queue.dequeue()} dequeued from queue`);
console.log(`${queue.dequeue()} dequeued from queue`);
// Display the front and rear elements of the queue
console.log("Front item is", queue.getFront());
console.log("Rear item is", queue.getRear());
Output
10 enqueued to queue
15 enqueued to queue
20 enqueued to queue
25 enqueued to queue
30 enqueued to queue
10 dequeued from queue
15 dequeued from queue
20 dequeued from queue
Front item is 25
Rear item is 30 Advantages of Array Implementation
- Easy to implement.
- A large amount of data can be managed efficiently with ease.
- Operations such as insertion and deletion can be performed with ease as a queue follows the
FIFOrule.
Limitations of Array Implementation
- The maximum size of the queue must be defined beforehand.
- The size of the array cannot be changed during the run time because it is not dynamic.
- If the queue has a large number of
enqueueanddequeueoperations, at some point (in case of linear increment offrontandrearindexes) it may happen that we may not be able to insert elements in the queue even if the queue is empty.
- Implementation of a Queue Using a Linked List
We discussed the disadvantages of array implementation above. Due to this, the array cannot be used for large-scale applications of queues. One of the solutions to overcome this limitation is linked list implementation of queues in data structures
The storage requirement of the linked representation of a queue with n elements is O(n). The time complexity of all the operations is the same i.e. O(1) here.
In a linked queue, each node of the queue consists of two parts i.e. data part and the link part. Each element of the queue points to its immediate next element in the memory. There are two pointers maintained in the memory i.e. front pointer and rear pointer. The front pointer contains the address of the starting element of the queue while the rear pointer contains the address of the last element of the queue.
Example of Queue Implementation in Different Languages Using a Linked List
#include
#include
typedef struct Node {
int data;
struct Node* next;
} Node;
typedef struct Queue {
Node* front;
Node* rear;
} Queue;
Queue* createQueue() {
Queue* queue = (Queue*)malloc(sizeof(Queue));
queue->front = queue->rear = NULL;
return queue;
}
void enqueue(Queue* queue, int data) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->data = data;
newNode->next = NULL;
if (queue->rear == NULL) {
queue->front = queue->rear = newNode;
return;
}
queue->rear->next = newNode;
queue->rear = newNode;
}
int dequeue(Queue* queue) {
if (queue->front == NULL) {
printf("Queue is empty\n");
return -1;
}
Node* temp = queue->front;
queue->front = queue->front->next;
if (queue->front == NULL) {
queue->rear = NULL;
}
int data = temp->data;
free(temp);
return data;
}
int peek(Queue* queue) {
return (queue->front != NULL) ? queue->front->data : -1;
}
int isEmpty(Queue* queue) {
return queue->front == NULL;
}
int main() {
Queue* queue = createQueue();
enqueue(queue, 10);
enqueue(queue, 20);
enqueue(queue, 30);
printf("%d dequeued from queue\n", dequeue(queue));
printf("Front item is %d\n", peek(queue));
return 0;
}
#include
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int value) : data(value), next(nullptr) {}
};
class Queue {
private:
Node* front;
Node* rear;
int size;
public:
Queue() : front(nullptr), rear(nullptr), size(0) {}
void enqueue(int data) {
Node* newNode = new Node(data);
if (rear == nullptr) {
front = rear = newNode;
return;
}
rear->next = newNode;
rear = newNode;
size++;
}
int dequeue() {
if (front == nullptr) {
cout << "Queue is empty" << endl;
return -1;
}
Node* temp = front;
front = front->next;
if (front == nullptr) {
rear = nullptr;
}
int data = temp->data;
delete temp;
size--;
return data;
}
int peek() {
return (front != nullptr) ? front->data : -1;
}
bool isEmpty() {
return front == nullptr;
}
~Queue() {
while (!isEmpty()) {
dequeue();
}
}
};
// Example usage
int main() {
Queue queue;
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
cout << queue.dequeue() << " dequeued from queue" << endl;
cout << "Front item is " << queue.peek() << endl;
return 0;
}
using System;
public class Node
{
public int Data;
public Node Next;
public Node(int data)
{
Data = data;
Next = null;
}
}
public class Queue
{
private Node front;
private Node rear;
public Queue()
{
front = rear = null;
}
public void Enqueue(int data)
{
Node newNode = new Node(data);
if (rear == null)
{
front = rear = newNode;
return;
}
rear.Next = newNode;
rear = newNode;
}
public int Dequeue()
{
if (front == null)
{
Console.WriteLine("Queue is empty");
return -1;
}
Node temp = front;
front = front.Next;
if (front == null)
{
rear = null;
}
int data = temp.Data;
return data;
}
public int Peek()
{
return (front != null) ? front.Data : -1;
}
public bool IsEmpty()
{
return front == null;
}
}
public class Program
{
public static void Main()
{
Queue queue = new Queue();
queue.Enqueue(10);
queue.Enqueue(20);
queue.Enqueue(30);
Console.WriteLine($"{queue.Dequeue()}");
Console.WriteLine($"{queue.Peek()}");
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
class Queue:
def __init__(self):
self.front = self.rear = None
self.size = 0
def enqueue(self, data):
new_node = Node(data)
if not self.rear:
self.front = self.rear = new_node
else:
self.rear.next = new_node
self.rear = new_node
self.size += 1
def dequeue(self):
if not self.front:
print("Queue is empty")
return None
temp = self.front
self.front = self.front.next
if not self.front:
self.rear = None
self.size -= 1
return temp.data
def peek(self):
return self.front.data if self.front else None
def is_empty(self):
return self.size == 0
# Example usage
queue = Queue()
queue.enqueue(10)
queue.enqueue(20)
queue.enqueue(30)
print(queue.dequeue()) # 10
print(queue.peek()) # 20
class Node {
int data;
Node next;
public Node(int data) {
this.data = data;
this.next = null;
}
}
class Queue {
private Node front, rear;
public Queue() {
this.front = this.rear = null;
}
void enqueue(int data) {
Node newNode = new Node(data);
if (this.rear == null) {
this.front = this.rear = newNode;
return;
}
this.rear.next = newNode;
this.rear = newNode;
}
int dequeue() {
if (this.front == null) {
System.out.println("Queue is empty");
return -1;
}
Node temp = this.front;
this.front = this.front.next;
if (this.front == null) {
this.rear = null;
}
int data = temp.data;
return data;
}
int peek() {
return (front != null) ? front.data : -1;
}
boolean isEmpty() {
return front == null;
}
}
public class Main {
public static void main(String[] args) {
Queue queue = new Queue();
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
System.out.println(queue.dequeue());
System.out.println(queue.peek());
}
}
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class Queue {
constructor() {
this.front = this.rear = null;
this.size = 0;
}
enqueue(data) {
const newNode = new Node(data);
if (!this.rear) {
this.front = this.rear = newNode;
} else {
this.rear.next = newNode;
this.rear = newNode;
}
this.size++;
}
dequeue() {
if (!this.front) {
console.log("Queue is empty");
return;
}
const temp = this.front;
this.front = this.front.next;
if (!this.front) {
this.rear = null;
}
this.size--;
return temp.data;
}
peek() {
return this.front ? this.front.data : null;
}
isEmpty() {
return this.size === 0;
}
}
// Example usage
const queue = new Queue();
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
console.log(queue.dequeue()); // 10
console.log(queue.peek()); // 20
Output
10
20
If you are facing any difficulty in understanding the linked list implementation of the queue in data structures refer to the previous tutorial, Linked Lists in Data Structures.
Complexity Analysis of Queue Operations

Applications of Queue in Data Structures
- Multi-programming: It is essential to organize the multiple programs running in the main memory so they are organized as queues.
- Network: In a network, a queue is used in devices such as a router or a switch.
- Job Scheduling: The computer has a task to execute a particular number of jobs that are scheduled to be executed one after another. These jobs are assigned to the processor one by one which is organized using a queue. E.g. CPU scheduling, Disk Scheduling
- Synchronization: The queue is used for synchronization when data is transferred asynchronously between two processes. E.g. IO Buffers, pipes, file IO, etc
- Interrupts: Handling of interrupts in real-time systems.
- Shared resources: Queues are used as waiting lists for a single shared resource.
- Operation on data structures: Certain operations like BFS (Breadth First Search), and tree traversal use Queue. The sequence of traversal of inputs is set using queues.
Advantages of Queue in Data Structures
- Efficient data processing: A queue can be used to efficiently process data in the order it was received. For example, in a computer system, a queue can be used to schedule processes in the order they were submitted.
- Resource management: A queue can be used to manage resources that are shared among multiple processes or threads. For example, a printer can use a queue to manage print jobs.
- Buffering: A queue can be used to buffer incoming data so that it can be processed at a later time. For example, a network device can use a queue to buffer incoming data packets before forwarding them to their destination.
- Memory management: A queue can be used to manage memory by allocating and deallocating memory blocks in sequential order.
Disadvantages of Queue Data Structures
- Limited flexibility: Queues follow a strict
FIFOorder, meaning the element that enters first is the first one to be removed. This lack of flexibility can be a disadvantage in some use cases where other priorities or requirements must be considered. - No random access: Unlike arrays or linked lists, queues do not allow random access to the elements. The user can only access the first element in the queue, and to access any other element, they need to remove all the elements that come before it. This can be a disadvantage when the user needs to access an element in the middle of the queue.
- Overhead: Queues require extra overhead to maintain the order of elements. Whenever an element is added or removed from the queue, all the other elements must be shifted accordingly, which can be time-consuming for large queues.
- Limited size: In some implementations, queues have a limited size, which can be a disadvantage when dealing with large amounts of data. Once the queue reaches its maximum size, it can no longer accept new elements.
- No search operation: Queues do not provide a search operation. The user cannot search for a specific element in the queue they can only remove the elements in the order they were added and hope to find the element they are looking for.
Summary
Queue is a fundamental data structure that ensures ordered processing and finds applications across a wide range of domains, from basic programming problems to complex system-level operations. Queues can be implemented using arrays, linked lists, or built-in libraries depending on the programming language. Queue in data structures is widely used in various applications , such as task scheduling, buffering, and handling asynchronous data.
Only 2% of Java Developers become Solution Architects. Don’t get left behind—Enroll now in our Java Architect Certification and secure your career growth & 60% higher salary potential.
FAQs
Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.












