Recursion in Data Structures: Recursive Function

Recursion in Data Structures: An Overview

You might have already come across recursion while learning Recursion in C and Recursion in C++. We even saw in the second tutorial, Data Structures and Algorithms, that recursion is a problem-solving technique in which a function calls itself.

In this DSA tutorial, we will see the recursion in detail i.e. its features, working, implementation, etc. To further enhance your understanding and application of recursion, consider enrolling in the Best Data Structures and Algorithms Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Recursion in Data Structures?

Recursion is the process in which a function calls itself again and again. It entails decomposing a challenging issue into more manageable issues and then solving each one again. There must be a terminating condition to stop such recursive calls. Recursion may also be called the alternative to iteration. Recursion provides us with an elegant way to solve complex problems, by breaking them down into smaller problems and with fewer lines of code than iteration.

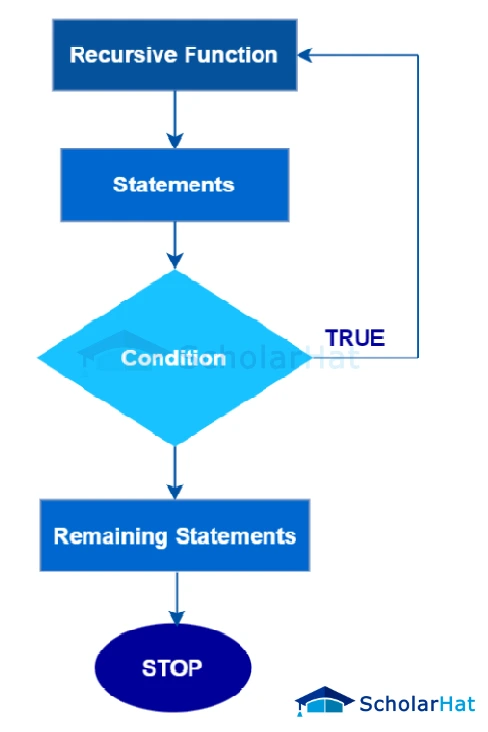
Recursive Function

A recursive function is a function that calls itself one or more times within its body. A recursive function solves a particular problem by calling a copy of itself and solving smaller subproblems of the original problems. Many more recursive calls can be generated as and when required. It is necessary to have a terminating condition or a base case in recursion, otherwise, these calls may go endlessly leading to an infinite loop of recursive calls and call stack overflow.

The recursive function uses the LIFO (LAST IN FIRST OUT) structure just like the stack data structure. A recursion tree is a diagram of the function calls connected by pointed(up or down) arrows to depict the order in which the calls were made.

Syntax to Declare a Recursive Function

recursionfunction()
{ 
recursionfunction(); //calling self function 
}

Format of Recursive Function

A recursive function consists of two things:

1. A base case, in which the recursion can terminate and return the result immediately.
2. A recursive case, in which the function is supposed to call itself, to break the current problem down into smaller problems.

Implementation of Recursion in Different Programming Languages

 
def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

n = 12
f = fibonacci(n)
print(f)
 

 
 public class Fibonacci {
    private static int[] memo;

    public static int fibonacci(int n) {
        if (n <= 1) {
            return n;
        }

        if (memo[n] != 0) {
            return memo[n];
        }

        memo[n] = fibonacci(n - 1) + fibonacci(n - 2);
        return memo[n];
    }

    public static void main(String[] args) {
        
        int n = 12;

        // Initialize memoization array
        memo = new int[n + 1];

        int f = fibonacci(n);
        System.out.println(f);
    }
}

 
 #include <iostream>
using namespace std;

int fibonacci(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return fibonacci(n - 1) + fibonacci(n - 2);
    }
}

int main() {
    int n, f;
    n=12;
    f = fibonacci(n);
    cout << f << endl;
    return 0;
}

Output

144

Properties of Recursion

1. It solves a problem by breaking it down into smaller sub-problems, each of which can be solved in the same way.
2. A recursive function must have a base case or stopping criteria to avoid infinite recursion.
3. Recursion involves calling the same function within itself, which leads to a call stack.
4. Recursive functions may be less efficient than iterative solutions in terms of memory and performance.

Read More - Best Data Structure Interview Questions and Answers

Applications of Recursion

1. Recursive solutions are best suited to some problems like:
   1. Tree Traversals: InOrder, PreOrder, PostOrder
   2. Graph Traversals: DFS [Depth First Search] and BFS [Breadth First Search]
   3. Tower of Hanoi
   4. Backtracking Algorithms
   5. Divide and Conquer Algorithms
   6. Dynamic Programming Problems
   7. Merge Sort, Quick Sort
   8. Binary Search
   9. Fibonacci Series, Factorial, etc.
2. Recursion is used in the design of compilers to parse and analyze programming languages.
3. Many computer graphics algorithms, such as fractals and the Mandelbrot set, use recursion to generate complex patterns.

Advantages of Recursion

1. Clarity and simplicity: Recursion can make code more readable and easier to understand. Recursive functions can be easier to read than iterative functions when solving certain types of problems, such as those that involve tree or graph structures.
2. Reducing code duplication: Recursive functions can help reduce code duplication by allowing a function to be defined once and called multiple times with different parameters.
3. Solving complex problems: Recursion can be a powerful technique for solving complex problems, particularly those that involve dividing a problem into smaller subproblems.
4. Flexibility: Recursive functions can be more flexible than iterative functions because they can handle inputs of varying sizes without needing to know the exact number of iterations required.

Disadvantages of Recursion

1. Performance Overhead: Recursive algorithms may have a higher performance overhead compared to iterative solutions. This is because each recursive call creates a new stack frame, which takes up additional memory and CPU resources. Recursion may also cause stack overflow errors if the recursion depth becomes too deep.
2. Difficult to Understand and Debug: Recursive algorithms can be difficult to understand and debug because they rely on multiple function calls, which can make the code more complex and harder to follow.
3. Memory Consumption: Recursive algorithms may consume a large amount of memory if the recursion depth is very deep.
4. Limited Scalability: Recursive algorithms may not scale well for very large input sizes because the recursion depth can become too deep and lead to performance and memory issues.
5. Tail Recursion Optimization: In some programming languages, tail recursion optimization is not supported, which means that tail recursive functions can be slow and may cause stack overflow errors

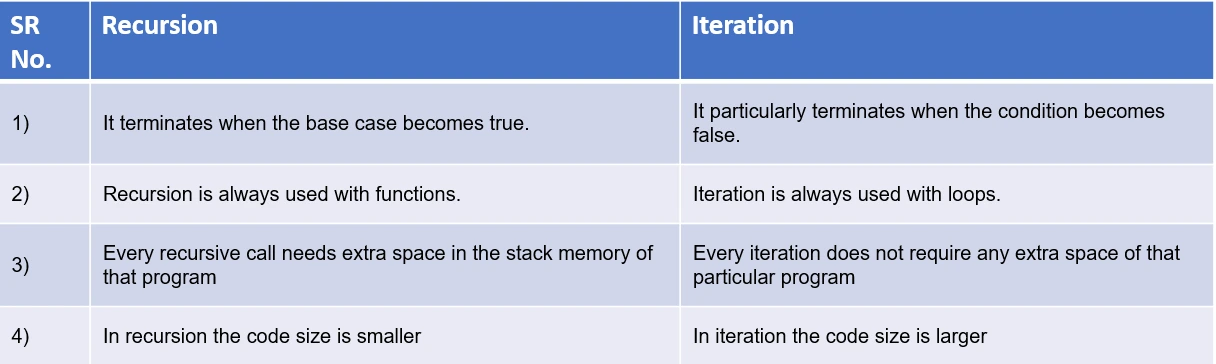
Difference between Recursion and Iteration

Summary

Recursion is a very useful approach when it comes to programming. It has wide applications ranging from calculating the factorial of a number to sorting and traversal algorithms. If you want to learn such an important concept in more depth, just consider our Dsa Training. It will prove a practical booster in your journey of programming.