Segment Tree in Data Structures: Operations, Advantages and Disadvantages

15 Jan 2025

Advanced

3.58K Views

43 min read

Segment Tree in Data Structures: An Overview

We saw that a Segment Tree is a tree data structure used for storing information about intervals, or segments in the section, Binary Trees in Data Structures. In this DSA tutorial, we will learn the Segment trees in detail with their properties, applications, etc. To further enhance your understanding and application of segment tree concepts, consider enrolling in the Dsa Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is a Segment Tree in Data Structures?

Segment Tree in Data Structures

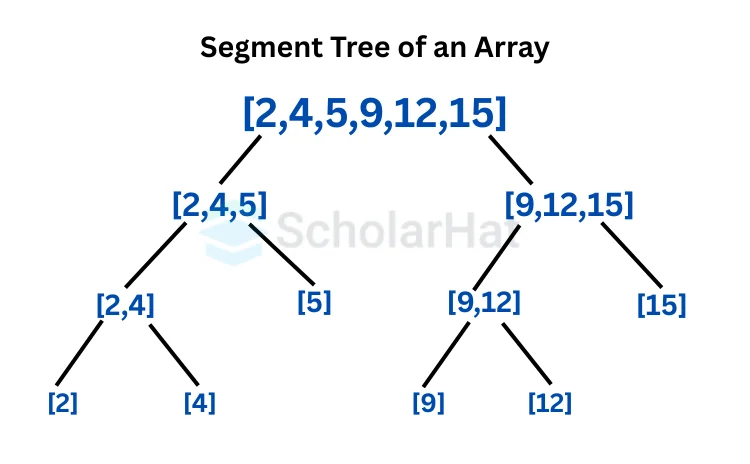
A segment tree is a binary tree used to process different range queries over an array or another linear data structure. It has a divide-and-conquer approach. It breaks down an array or ranges into smaller segments, each containing a subset of the original data, creating a tree-like hierarchy. Here, each node represents a segment or range of array elements.

The root of the tree is a complete segment, i.e. carries information related to all the elements of the array. For the next level, this data in root is divided into two halves. The first half is assigned to the left subtree or the left child and the other half to the right one. This procedure is followed by subsequent nodes, recursively. The leaves in the tree hold individual elements of the array.

Creating a Segment Tree in Data Structures


class SegmentTree:
    def __init__(self, V):
        self.arr = V
        self.tree = [0] * (4 * len(V))
        self.build_tree(1, 0, len(V) - 1)

    def build_tree(self, node, s, e):
        if s == e:
            self.tree[node] = self.arr[s]
            return self.arr[s]

        mid = s + (e - s) // 2
        self.tree[node] = self.build_tree(2 * node, s, mid) + self.build_tree(2 * node + 1, mid + 1, e)
        return self.tree[node]

    def print_segment_tree(self):
        print("Segment Tree:", end=" ")
        for value in self.tree:
            print(value, end=" ")
        print()


if __name__ == "__main__":
    input_array = [1, 2, 3, 4, 5]
    seg_tree = SegmentTree(input_array)

    # Now, the segment tree is built, and you can perform range queries and updates efficiently.

    # Print the segment tree
    seg_tree.print_segment_tree()


import java.util.Arrays;
import java.util.Vector;

public class SegmentTree {
    private Vector arr, tree;

    private int buildTree(int node, int s, int e) {
        if (s == e) {
            tree.setElementAt(arr.get(s), node);
            return arr.get(s);
        }

        int mid = s + (e - s) / 2;
        int leftSum = buildTree(2 * node, s, mid);
        int rightSum = buildTree(2 * node + 1, mid + 1, e);
        tree.setElementAt(leftSum + rightSum, node);
        return tree.get(node);
    }

    public SegmentTree(Vector V) {
        arr = V;
        int max_size = 4 * V.size();
        tree = new Vector<>(Arrays.asList(new Integer[max_size]));
        Arrays.fill(tree.toArray(), 0);

        buildTree(1, 0, V.size() - 1);
    }

    public void printSegmentTree() {
        System.out.print("Segment Tree: ");
        for (int value : tree) {
            System.out.print(value + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        // Example usage
        Vector inputArray = new Vector<>(Arrays.asList(1, 2, 3, 4, 5));
        SegmentTree segTree = new SegmentTree(inputArray);

        // Now, the segment tree is built, and you can perform range queries and updates efficiently.

        // Print the segment tree
        segTree.printSegmentTree();
    }
}


#include <iostream<
#include <vector<

using namespace std;

class SegmentTree {
private:
    vector arr, tree;

    int buildTree(int node, int s, int e) {
        if (s == e) {
            tree[node] = arr[s];
            return arr[s];
        }

        int m = s + (e - s) / 2;
        tree[node] = buildTree(node * 2, s, m) + buildTree(node * 2 + 1, m + 1, e);
        return tree[node];
    }

public:
    SegmentTree(const vector& V) {
        arr = V;
        int max_size = 4 * V.size();
        tree.resize(max_size);
        buildTree(1, 0, V.size() - 1);
    }

    void printSegmentTree() const {
        cout << "Segment Tree: ";
        for (int value : tree) {
            cout << value << " ";
        }
        cout << endl;
    }
};

int main() {
    // Example usage
    vector inputArray = {1, 2, 3, 4, 5};
    SegmentTree segTree(inputArray);

    // Now, the segment tree is built, and you can perform range queries and updates efficiently.
    
    // Print the segment tree
    segTree.printSegmentTree();

    return 0;
}

Output

Segment Tree: 0 15 6 9 3 3 4 5 1 2 0 0 0 0 0 0 0 0 0 0

Operations of Segment Trees

1) Update

The update operation takes in the new value to be set and the corresponding index. After making the update to the tree array, it needs to make similar relevant changes to the actual segment tree.

Example to perform update operation on Segment Trees


def update(tree, index, start, end, updateIndex, value):
    if start == end:
        # Leaf node, update the value
        tree[index] = value
    else:
        mid = (start + end) // 2

        # If the update index is in the left subtree
        if updateIndex <= mid:
            update(tree, 2 * index + 1, start, mid, updateIndex, value)
        else:
            # If the update index is in the right subtree
            update(tree, 2 * index + 2, mid + 1, end, updateIndex, value)

        # Recalculate the parent node value after updating the child nodes
        tree[index] = tree[2 * index + 1] + tree[2 * index + 2]


def query(tree, index, start, end, queryStart, queryEnd):
    if queryStart > end or queryEnd < start:
        # The range is completely outside the current node's range
        return 0
    elif queryStart <= start and queryEnd >= end:
        # The range is completely inside the current node's range
        return tree[index]
    else:
        mid = (start + end) // 2

        # Recursively query the left and right subtrees
        leftSum = query(tree, 2 * index + 1, start, mid, queryStart, queryEnd)
        rightSum = query(tree, 2 * index + 2, mid + 1, end, queryStart, queryEnd)

        return leftSum + rightSum


arr = [1, 3, 5, 7, 9, 11]

# Build the segment tree
n = len(arr)
tree = [0] * (4 * n)
for i in range(n):
    update(tree, 0, 0, n - 1, i, arr[i])

# Print the segment tree
print("Segment Tree:", end=" ")
for i in tree:
    print(i, end=" ")
print()

# Perform an update operation
updateIndex = 2  # Index to update
newValue = 6  # New value to assign
update(tree, 0, 0, n - 1, updateIndex, newValue)

# Print the updated segment tree
print("Updated Segment Tree:", end=" ")
for i in tree:
    print(i, end=" ")
print()

# Perform a range sum query
queryStart = 1  # Query start index
queryEnd = 4  # Query end index
summation = query(tree, 0, 0, n - 1, queryStart, queryEnd)

print(f"Sum from index {queryStart} to {queryEnd}: {summation}")


import java.util.Arrays;

class Main {
    // Function to update a value in the segment tree
    static void update(int[] tree, int index, int start, int end, int updateIndex, int value) {
        if (start == end) {
            // Leaf node, update the value
            tree[index] = value;
        } else {
            int mid = (start + end) / 2;

            // If the update index is in the left subtree
            if (updateIndex <= mid) {
                update(tree, 2 * index + 1, start, mid, updateIndex, value);
            } else {
                // If the update index is in the right subtree
                update(tree, 2 * index + 2, mid + 1, end, updateIndex, value);
            }
        }

        // Recalculate the parent node value after updating the child nodes
        tree[index] = tree[2 * index + 1] + tree[2 * index + 2];
    }

    // Function to perform a range sum query in the segment tree
    static int query(int[] tree, int index, int start, int end, int queryStart, int queryEnd) {
        if (queryStart > end || queryEnd < start) {
            // The range is completely outside the current node's range
            return 0;
        } else if (queryStart <= start && queryEnd >= end) {
            // The range is completely inside the current node's range
            return tree[index];
        } else {
            int mid = (start + end) / 2;

            // Recursively query the left and right subtrees
            int leftSum = query(tree, 2 * index + 1, start, mid, queryStart, queryEnd);
            int rightSum = query(tree, 2 * index + 2, mid + 1, end, queryStart, queryEnd);

            return leftSum + rightSum;
        }
    }

    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, 9, 11};

        // Build the segment tree
        int n = arr.length;
        int[] tree = new int[4 * n];
        Arrays.fill(tree, 0);
        for (int i = 0; i < n; ++i) {
            update(tree, 0, 0, n - 1, i, arr[i]);
        }

        // Print the segment tree
        System.out.print("Segment Tree: ");
        for (int i = 0; i < tree.length; ++i) {
            System.out.print(tree[i] + " ");
        }
        System.out.println();

        // Perform an update operation
        int updateIndex = 2; // Index to update
        int newValue = 6; // New value to assign
        update(tree, 0, 0, n - 1, updateIndex, newValue);

        // Print the updated segment tree
        System.out.print("Updated Segment Tree: ");
        for (int i = 0; i < tree.length; ++i) {
            System.out.print(tree[i] + " ");
        }
        System.out.println();

        // Perform a range sum query
        int queryStart = 1; // Query start index
        int queryEnd = 4; // Query end index
        int sum = query(tree, 0, 0, n - 1, queryStart, queryEnd);

        System.out.println("Sum from index " + queryStart + " to " + queryEnd + ": " + sum);
    }
}



 #include <iostream>
 #include <vector>
 
 using namespace std;
 
 // Function to update a value in the segment tree
 void update(vector& tree, int index, int start, int end, int updateIndex, int value) {
   if (start == end) {
     // Leaf node, update the value
     tree[index] = value;
   } else {
     int mid = (start + end) / 2;
 
     // If the update index is in the left subtree
     if (updateIndex <= mid) {
       update(tree, 2 * index + 1, start, mid, updateIndex, value);
     } else {
       // If the update index is in the right subtree
       update(tree, 2 * index + 2, mid + 1, end, updateIndex, value);
     }
 
     // Recalculate the parent node value after updating the child nodes
     tree[index] = tree[2 * index + 1] + tree[2 * index + 2];
   }
 }
 
 // Function to perform a range sum query in the segment tree
 int query(vector& tree, int index, int start, int end, int queryStart, int queryEnd) {
   if (queryStart > end || queryEnd < start) {
     // The range is completely outside the current node's range
     return 0;
   } else if (queryStart <= start && queryEnd >= end) {
     // The range is completely inside the current node's range
     return tree[index];
   } else {
     int mid = (start + end) / 2;
 
     // Recursively query the left and right subtrees
     int leftSum = query(tree, 2 * index + 1, start, mid, queryStart, queryEnd);
     int rightSum = query(tree, 2 * index + 2, mid + 1, end, queryStart, queryEnd);
 
     return leftSum + rightSum;
   }
 }
 
 int main() {
   vector arr = {1, 3, 5, 7, 9, 11};
 
   // Build the segment tree
   int n = arr.size();
   vector tree(4 * n);
   for (int i = 0; i < n; ++i) {
     update(tree, 0, 0, n - 1, i, arr[i]);
   }
 
   // Print the segment tree
   cout << "Segment Tree: ";
   for (int i = 0; i < tree.size(); ++i) {
     cout << tree[i] << " ";
   }
   cout << endl;
 
   // Perform an update operation
   int updateIndex = 2; // Index to update
   int newValue = 6; // New value to assign
   update(tree, 0, 0, n - 1, updateIndex, newValue);
 
   // Print the updated segment tree
   cout << "Updated Segment Tree: ";
   for (int i = 0; i < tree.size(); ++i) {
     cout << tree[i] << " ";
   }
   cout << endl;
 
   // Perform a range sum query
   int queryStart = 1; // Query start index
   int queryEnd = 4; // Query end index
   int sum = query(tree, 0, 0, n - 1, queryStart, queryEnd);
 
   cout << "Sum from index " << queryStart << " to " << queryEnd << ": " << sum << endl;
 
   return 0;
 }

Output

Segment Tree: 36 9 27 4 5 16 11 1 3 0 0 7 9 0 0 0 0 0 0 0 0 0 0 0 
Updated Segment Tree: 37 10 27 4 6 16 11 1 3 0 0 7 9 0 0 0 0 0 0 0 0 0 0 0 
Sum from index 1 to 4: 25

2) Query

The query() function takes in as parameters the boundaries of the query, l and r, and returns the sum of the elements in this range of l and r in the array.

Example to perform query operation on Segment Trees


import math

def buildSegmentTree(arr, segmentTree, low, high, pos):
    if low == high:
        segmentTree[pos] = arr[low]
        return
    mid = low + (high - low) // 2
    buildSegmentTree(arr, segmentTree, low, mid, 2 * pos + 1)
    buildSegmentTree(arr, segmentTree, mid + 1, high, 2 * pos + 2)
    segmentTree[pos] = segmentTree[2 * pos + 1] + segmentTree[2 * pos + 2]

def query(segmentTree, qlow, qhigh, low, high, pos):
    if qlow <= low and qhigh >= high:
        return segmentTree[pos]
    if qlow > high or qhigh < low:
        return 0
    mid = low + (high - low) // 2
    return query(segmentTree, qlow, qhigh, low, mid, 2 * pos + 1) + query(segmentTree, qlow, qhigh, mid + 1, high, 2 * pos + 2)

# Example usage
arr = [1, 3, 5, 7, 9, 11]
n = len(arr)

# Calculate the size of the segment tree
treeSize = 2 * (2 ** (math.ceil(math.log2(n)))) - 1

# Create the segment tree
segmentTree = [0] * treeSize

# Build the segment tree
buildSegmentTree(arr, segmentTree, 0, n - 1, 0)

# Perform a query (example range [2, 4])
qlow, qhigh = 2, 4
summation = query(segmentTree, qlow, qhigh, 0, n - 1, 0)
print("Sum of elements in the given range:", summation)


import java.util.Arrays;

class Main {
    // Function to build the segment tree
    static void buildSegmentTree(int[] arr, int[] segmentTree, int low, int high, int pos) {
        if (low == high) {
            segmentTree[pos] = arr[low];
            return;
        }

        int mid = low + (high - low) / 2;
        buildSegmentTree(arr, segmentTree, low, mid, 2 * pos + 1);
        buildSegmentTree(arr, segmentTree, mid + 1, high, 2 * pos + 2);
        segmentTree[pos] = segmentTree[2 * pos + 1] + segmentTree[2 * pos + 2];
    }

    // Function to perform the query operation
    static int query(int[] segmentTree, int qlow, int qhigh, int low, int high, int pos) {
        if (qlow <= low && qhigh >= high) {
            return segmentTree[pos];
        }

        if (qlow > high || qhigh < low) {
            return 0;
        }

        int mid = low + (high - low) / 2;
        return query(segmentTree, qlow, qhigh, low, mid, 2 * pos + 1) +
                query(segmentTree, qlow, qhigh, mid + 1, high, 2 * pos + 2);
    }

    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, 9, 11};
        int n = arr.length;

        // Calculate the size of the segment tree
        int treeSize = 2 * (int)Math.pow(2, Math.ceil(Math.log(n) / Math.log(2))) - 1;

        // Create the segment tree
        int[] segmentTree = new int[treeSize];

        // Build the segment tree
        buildSegmentTree(arr, segmentTree, 0, n - 1, 0);

        // Perform a query (example range [2, 4])
        int qlow = 2, qhigh = 4;
        int sum = query(segmentTree, qlow, qhigh, 0, n - 1, 0);
        System.out.println("Sum of elements in the given range: " + sum);
    }
}


#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

void buildSegmentTree(const vector& arr, vector& segmentTree, int low, int high, int pos) {
    if (low == high) {
        segmentTree[pos] = arr[low];
        return;
    }

    int mid = low + (high - low) / 2;
    buildSegmentTree(arr, segmentTree, low, mid, 2 * pos + 1);
    buildSegmentTree(arr, segmentTree, mid + 1, high, 2 * pos + 2);
    segmentTree[pos] = segmentTree[2 * pos + 1] + segmentTree[2 * pos + 2];
}

int query(const vector& segmentTree, int qlow, int qhigh, int low, int high, int pos) {
    if (qlow <= low && qhigh >= high) {
        return segmentTree[pos];
    }

    if (qlow > high || qhigh < low) {
        return 0;
    }

    int mid = low + (high - low) / 2;
    return query(segmentTree, qlow, qhigh, low, mid, 2 * pos + 1) + query(segmentTree, qlow, qhigh, mid + 1, high, 2 * pos + 2);
}

int main() {
    vector arr = {1, 3, 5, 7, 9, 11};
    int n = arr.size();

    // Calculate the size of the segment tree
    int treeSize = 2 * (int)pow(2, ceil(log2(n))) - 1;

    // Create the segment tree
    vector segmentTree(treeSize);

    // Build the segment tree
    buildSegmentTree(arr, segmentTree, 0, n - 1, 0);

    // Perform a query (example range [2, 4])
    int qlow = 2, qhigh = 4;
    int sum = query(segmentTree, qlow, qhigh, 0, n - 1, 0);
    cout << "Sum of elements in the given range: " << sum << endl;

    return 0;
}

Output

Sum of elements in the given range: 21

Complexity Analysis of Operations on Segment Trees

Time Complexity
Operations Time Complexity
Construction O(n)
Query O(log n)
Update O(log n)
Space Complexity: The space complexity of a segment tree is O(n).

Here n is the number of elements put in the tree

Advantages of Segment Trees

Efficient Range Queries: Segment trees excel at performing range queries on dynamic arrays or sequences. They allow you to answer queries about a specific range of elements in logarithmic time complexity O(log n), regardless of the size of the array.
Dynamic Updates: Segment trees can efficiently handle updates to the elements of an array or sequence. Whether it's modifying a single element or updating a range of values, segment trees can perform these updates in logarithmic time complexity.
Versatility: Segment trees are flexible and adaptable. They can be used for various types of data, such as integers, floating-point numbers, or even non-numeric values, as long as you define appropriate operations for the data type.
Space Efficiency: Although segment trees require additional memory to store the tree structure, they typically provide a space-efficient solution.
Range Decomposition: Segment trees naturally decompose an array or sequence into smaller segments, allowing for efficient recursive processing. This property makes them useful in divide-and-conquer algorithms, where problems are divided into smaller subproblems, solved recursively, and then combined to obtain the final result.

Disadvantages of Segment Trees

Space Complexity: Segment trees require additional space to store the tree structure, which can be a disadvantage in scenarios where memory usage is a concern.
Construction Time: Building a segment tree can take a significant amount of time, especially when the input array is large. The construction process involves recursively dividing the array into smaller segments and performing operations to build the tree.
Updates and Modifications: Although segment trees excel at querying and computing aggregate functions over a range of elements efficiently, updating or modifying individual elements can be more time-consuming. When an element in the input array changes, the corresponding segment tree needs to be updated to reflect the modification, which can require traversing multiple tree nodes.
Complex Implementation: Implementing a segment tree can be challenging compared to simpler data structures. The recursive nature of segment trees and the need for efficient indexing can make the code more intricate and error-prone.

Summary

So, here we saw all the aspects of segment trees in data structures. It's quite a difficult concept and hence requires a good amount of time to understand the concepts. To test your knowledge of segment trees, enroll in our Free Best Dsa Course.

FAQs

A segment tree is a binary tree used to process different range queries over an array or another linear data structure.

O(log n) is the time complexity of query operation on Segment Trees.

The construction process involves recursively dividing the array into smaller segments and performing operations to build the tree.

01 Career Opportunities

02 Beginner

03 Intermediate

04 Advanced

05 Questions

06 Training Programs

Segment Tree in Data Structures: Operations, Advantages and Disadvantages

Free DSA Online Course with Certification

Segment Tree in Data Structures: An Overview

What is a Segment Tree in Data Structures?

Creating a Segment Tree in Data Structures

Output

Operations of Segment Trees

1) Update

Example to perform update operation on Segment Trees

Output

2) Query

Example to perform query operation on Segment Trees

Output

Complexity Analysis of Operations on Segment Trees

Advantages of Segment Trees

Disadvantages of Segment Trees

Summary

FAQs

About Author

Live Batches Schedule View All

Live Batches Schedule View All

Operations	Time Complexity
Construction	O(n)
Query	O(log n)
Update	O(log n)

01 Career Opportunities

02 Beginner

03 Intermediate

04 Advanced

05 Questions

06 Training Programs

Segment Tree in Data Structures: Operations, Advantages and Disadvantages

Free DSA Online Course with Certification

Segment Tree in Data Structures: An Overview

What is a Segment Tree in Data Structures?

Creating a Segment Tree in Data Structures

Output

Operations of Segment Trees

1) Update

Example to perform update operation on Segment Trees

Output

2) Query

Example to perform query operation on Segment Trees

Output

Complexity Analysis of Operations on Segment Trees

Advantages of Segment Trees

Disadvantages of Segment Trees

Summary

FAQs

Q1. What is a segment tree?

Q2. What is the time complexity of query operation on Segment Trees?

Q3. How is a segment tree constructed?

About Author

Live Batches Schedule View All

Live Batches Schedule View All