Binary Search in Data Structures

Binary Search: An Overview

In this DSA tutorial, we are going to look in detail at the Binary Search. We will learn its features, working, implementation, etc. To further enhance your understanding and application of binary search concepts, consider enrolling in the best Data Structures And Algorithms Certification to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Binary Search in Data Structures?

This search technique involves dividing a large dataset into smaller subsets until the desired item is found. It repeatedly divides in half the portion of the list and tries to find the element in one or the other half until the element is found or the array is exhausted. Thus, the element is always searched in the middle portion of an array

Binary Search Algorithm

Step: 1 Start by defining the search interval/space: the entire array or list in the beginning.
Step: 2 Divide the search space into two halves by finding the midpoint. 
Step: 3 Compare the middle element of the search space with the key. 
Step: 4 If the key matches with the middle element, the search is complete and the index of the value is returned. The process is terminated.
Step: 5 If the key does not match with the middle element, choose which half will be used as the next search space.
           If the key is smaller than the middle element, the left half is used for the next search.
           If the key is larger than the middle element, the right side is used for the next search.
Step: 6 Again start with step 2.
Step: 7 This process is continued until the key is found or the total search space is exhausted.    

Working of Binary Search Algorithm in Data Structures

1. Set two pointers low and high at the lowest and the highest positions respectively.

   

2. Find the middle element mid of the array ie. arr[(low + high)/2] = arr[(0+6)]/2] = arr[3] = 44

   

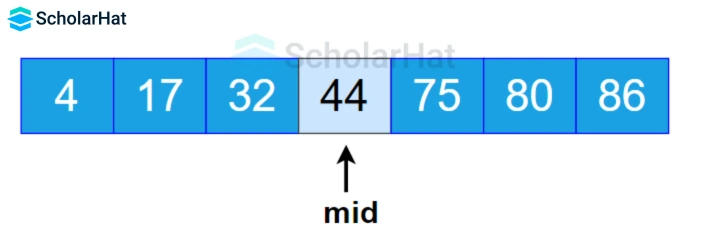
3. If the element key == mid, return the index of mid. Otherwise, compare the element to be searched with mid.
   • If key > mid, compare the key with the middle element of the elements on the right side of mid. This is done by setting low to low = mid+1.
   • Otherwise, compare the key with the middle element of the elements on the left side of mid. This is done by setting high to high = mid-1.

   

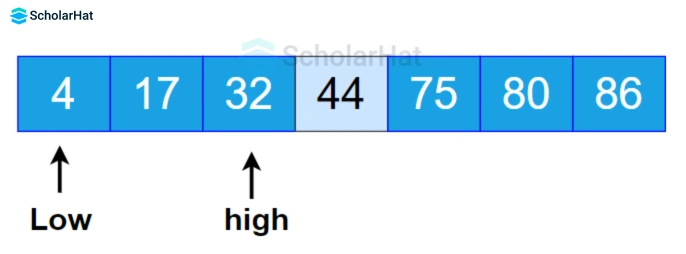
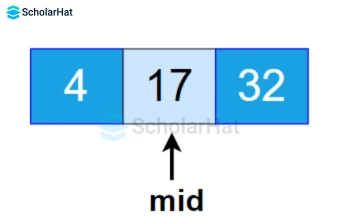
4. Repeat steps 2 to 3 until low meets high.

   

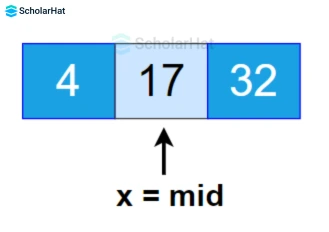
5. key = 17 is found.

   

Read More - DSA Interview Questions and Answers

Implementation of Binary Search Algorithm in Different Programming Languages

1. Recursive Binary Search

Recursive Binary Search Algorithm

binarySearch(arr, key, low, high)
    if low > high
        return False 
    else
        mid = (low + high) / 2 
        if key == arr[mid]
            return mid
        else if key > arr[mid]        // key is on the right side
            return binarySearch(arr, key, mid + 1, high)
        else                               // key is on the left side
            return binarySearch(arr, key, low, mid - 1)    

Example of Recursive Binary Search Algorithm in Different Languages

def binarySearch(array, key, low, high):
    if high >= low:
        mid = low + (high - low) // 2

        # If found at mid, then return it
        if array[mid] == key:
            return mid

        # Search the left half
        if array[mid] > key:
            return binarySearch(array, key, low, mid - 1)

        # Search the right half
        return binarySearch(array, key, mid + 1, high)

    return -1

array = [4, 17, 32, 44, 75, 80, 86]
print("The array to be searched is: ", array)

key = 80
n = len(array)
result = binarySearch(array, key, 0, n - 1)

if result == -1:
    print("Not found")
else:
    print("Element is found at index", result)
    

import java.util.Arrays;

public class BinarySearch {
    static int binarySearch(int[] array, int key, int low, int high) {
        if (high >= low) {
            int mid = low + (high - low) / 2;

            // If found at mid, then return it
            if (array[mid] == key) {
                return mid;
            }

            // Search the left half
            if (array[mid] > key) {
                return binarySearch(array, key, low, mid - 1);
            }

            // Search the right half
            return binarySearch(array, key, mid + 1, high);
        }

        return -1;
    }

    public static void main(String[] args) {
        int[] array = {4, 17, 32, 44, 75, 80, 86};
        
        System.out.print("The array to be searched is: ");
        System.out.println(Arrays.toString(array));

        int key = 80;
        int n = array.length;
        int result = binarySearch(array, key, 0, n - 1);

        if (result == -1) {
            System.out.println("Not found");
        } else {
            System.out.println("Element is found at index " + result);
        }
    }
}
    

#include <iostream>
using namespace std;

int binarySearch(int array[], int key, int low, int high) {
  if (high >= low) {
    int mid = low + (high - low) / 2;

    // If found at mid, then return it
    if (array[mid] == key)
      return mid;

    // Search the left half
    if (array[mid] > key)
      return binarySearch(array, key, low, mid - 1);

    // Search the right half
    return binarySearch(array, key, mid + 1, high);
  }

  return -1;
}

int main(void) {
  int array[] = {4, 17, 32, 44, 75, 80, 86};
  cout << "The array to be searched is: ";
    for (int i : array) {
      cout << i << ", ";
    }
  cout << std::endl;
  int key = 80;
  int n = sizeof(array) / sizeof(array[0]);
  int result = binarySearch(array, key, 0, n - 1);
  if (result == -1)
    printf("Not found");
  else
    printf("Element is found at index %d", result);
    

Output

The array to be searched is: 4, 17, 32, 44, 75, 80, 86, 
Element is found at index 5 

2. Iterative Binary Search

Iterative Binary Search Algorithm

do until the pointers low and high meet each other.
    mid = (low + high)/2
    if (x == arr[mid])
        return mid
    else if (x > arr[mid]) // x is on the right side
        low = mid + 1
    else                       // x is on the left side
        high = mid - 1 

Example of Iterative Binary Search Algorithm in Different Languages

def binarySearch(array, key, low, high):
    while low <= high:
        mid = low + (high - low) // 2

        if array[mid] == key:
            return mid

        if array[mid] < key:
            low = mid + 1
        else:
            high = mid - 1

    return -1

array = [4, 17, 32, 44, 75, 80, 86]
print("The array to be searched is:", end=" ")
print(*array, sep=", ")
key = 32
result = binarySearch(array, key, 0, len(array) - 1)
if result == -1:
    print("Not found")
else:
    print(f"Element {key} is found at index {result}")
    

public class BinarySearch {
    static int binarySearch(int[] array, int key, int low, int high) {
        while (low <= high) {
            int mid = low + (high - low) / 2;

            if (array[mid] == key)
                return mid;

            if (array[mid] < key)
                low = mid + 1;
            else
                high = mid - 1;
        }

        return -1;
    }

    public static void main(String[] args) {
        int[] array = {4, 17, 32, 44, 75, 80, 86};
        System.out.print("The array to be searched is: ");
        for (int i : array) {
            System.out.print(i + ", ");
        }
        System.out.println();
        int key = 32;
        int result = binarySearch(array, key, 0, array.length - 1);
        if (result == -1)
            System.out.println("Not found");
        else
            System.out.println("Element " + key + " is found at index " + result);
    }
}
    

#include <iostream>
using namespace std;

int binarySearch(int array[], int key, int low, int high) {
    while (low <= high) {
        int mid = low + (high - low) / 2;

        if (array[mid] == key)
            return mid;

        if (array[mid] < key)
            low = mid + 1;
        else
            high = mid - 1;
    }

    return -1;
}

int main(void) {
    int array[] = {4, 17, 32, 44, 75, 80, 86};
    cout << "The array to be searched is: ";
    for (int i : array) {
        cout << i << ", ";
    }
    cout << endl;
    int key = 32;
    int n = sizeof(array) / sizeof(array[0]);
    int result = binarySearch(array, key, 0, n - 1);
    if (result == -1)
        printf("Not found");
    else
        printf("Element %d is found at index %d", key, result);

    return 0;
}
    

Output

The array to be searched is: 4, 17, 32, 44, 75, 80, 86, 
Element 32 is found at index 2   

Binary Search Complexity Analysis

1. Time Complexity

   Case	Time Complexity
   Best Case	O(1)
   Average Case	O(log n)
   Worst Case	O(log n)

2. Space Complexity: As we are not using any significant extra memory in Binary Search, the space complexity is constant, i.e. O(1).

Applications of Binary Search

1. In libraries of Java, .Net, C++ STL.
2. The binary search is used to pinpoint the place where the error happens while debugging.
3. It can serve as a building block for complicated machine learning algorithms, such as those for training neural networks.
4. It can be used to search in computer graphics algorithms like ray tracing or texture mapping.
5. It can be applied to database searches.

Advantages of Binary Search

1. It is faster than linear search, especially for large arrays since its run time complexity is O(logN).
2. More efficient than other searching algorithms with a similar time complexity, such as interpolation search or exponential search.
3. At each iteration, the binary search algorithm eliminates half of the list and significantly reduces the search space.
4. Binary search is well-suited for searching large datasets that are stored in external memory, such as on a hard drive or in the cloud.
5. It even works on a rotated array.

Disadvantages of Binary Search

1. Binary search requires that the array be sorted before the algorithm is applied. If the array is not sorted, then the algorithm cannot be used.
2. Binary search requires that the data structure being searched be stored in contiguous memory locations.
3. If the array is being updated dynamically, i.e., new elements are added or old elements are deleted, then the binary search cannot be used as it requires the array to be static.
4. It requires that the elements of the array be comparable, meaning that they must be able to be ordered.
5. The recursive binary search method uses stack space.

Summary