Merge Sort in Data Structures and Algorithms: With Implementation in C++/Java/Python

Merge Sort in Data Structures: An Overview

Merge Sort in Data Structures is one of the most popular and efficient recursive sorting algorithms. It divides the given list into two halves, sorts them, and then merges the two sorted halves. In this DSA tutorial, we will understand the Merge Sort algorithm, its underlying approach, implementation, complexity, etc. Consider enrolling in Data Structures And Algorithms Certification, where you can gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is the Merge Sort Algorithm in Data Structures?

Merge sort involves dividing a given list into smaller sub-lists, sorting them, and then combining the sorted sub-lists back into a larger, sorted list. It works by dividing the array repeatedly to make several single-element arrays. The concept of merge sort involves breaking down an array of n elements into n individual elements. This divide-and-conquer approach ensures that the algorithm is efficient for large data sets.

Divide and Conquer: The Underlying Principle

Merge Sort operates according to the Divide and Conquer strategy.

In this technique, a problem is divided into sub-problems. Each sub-problem is solved individually to find the solution. Finally, the results of the sub-problems are combined to form the final solution.

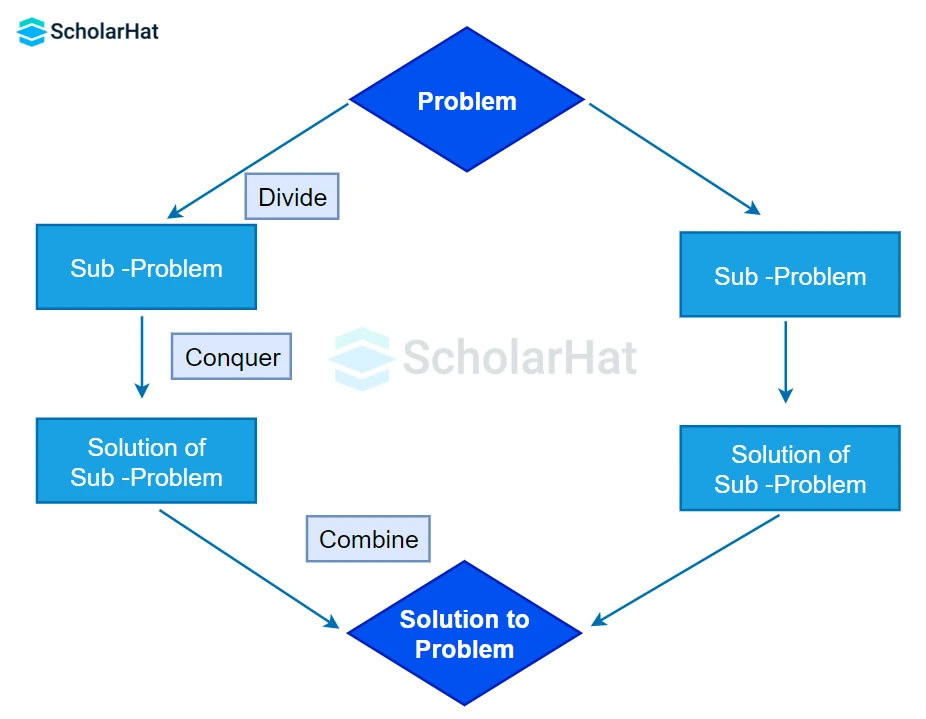
Let us understand with an example.

Suppose we need to sort this unsorted array, A={31, 16, 11, 30, 24, 39, 7}. A subproblem would be to sort a sub-section of this array starting at index p and ending at index r, denoted as A[p..r].

1. Divide: we find the midpoint of the given array by using the formula mid=p+(r-p)/2. Here the midpoint is 3. Now, we can split the subarray A[p..r] into two arrays A[p..mid] and A[mid+1, r] i.e A[31, 16, 11, 30] and A[24, 39, 7].
2. Conquer: We recursively keep dividing the array and keep calculating the midpoint for doing the same. It is important to note that a single array element is always sorted. We will keep dividing till all elements in the array become single array elements. Hence, this is the base case i.e. when there are n subarrays of the original array that consisted of n integers.

   

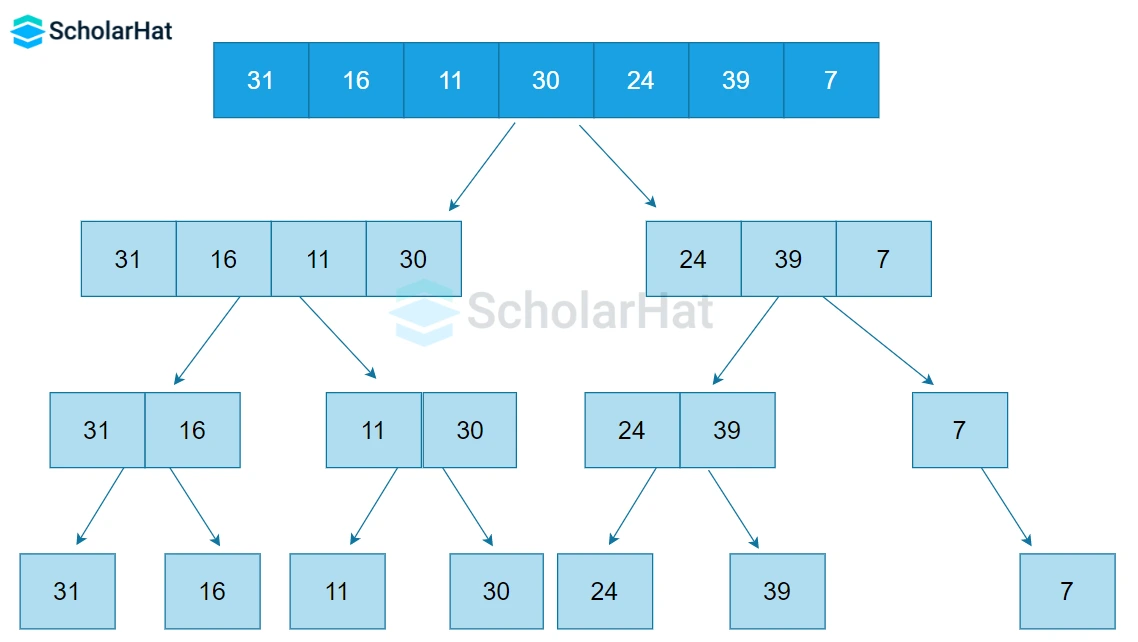
3. Combine: Now that all our subarrays are formed, it is time to combine them in sorted order.

   

Read More - DSA Interview Questions and Answers

Merge Sort Algorithm

The MergeSort function repeatedly divides the array into two halves until we reach a stage where we try to perform MergeSort on a subarray of size 1 i.e. p == r. After that, the merge function comes into play and combines the sorted arrays into larger arrays until the whole array is merged.

To sort an entire array, we need to call MergeSort(A, 0, length(A)-1)

MergeSort(A, p, r):
    if p > r 
        return
    mid = (p+r)/2
    mergeSort(A, p, mid)
    mergeSort(A, mid+1, r)
    merge(A, p, mid, r)   

The merge Step of Merge Sort

It is the most important part of the merge sort algorithm. The merge step merges two sorted lists(arrays) to build one large sorted list(array). The algorithm maintains three-pointers, one for each of the two arrays and one for maintaining the current index of the final sorted array. Our task is to merge two subarrays A[p..mid] and A[mid+1..r] to create a sorted array A[p..r]. So the inputs to the function are A, p, q mid, r

The merge() function works as follows:

1. Create copies of the subarrays L <- A[p..q] and M <- A[q+1..r].
2. Create three pointers i, j, and k
   • i maintains the current index of L, starting at 1
   • j maintains the current index of M, starting at 1
   • k maintains the current index of A[p..q], starting at p.
3. Until we reach the end of either L or M, pick the larger among the elements from L and M and place them in the correct position at A[p..q]
4. When we run out of elements in either L or M, pick up the remaining elements and put them in A[p..q]

Implementation of Merge Sort in Different Languages in Data Structures

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        M = arr[mid:]

        merge_sort(L)
        merge_sort(M)

        i = j = k = 0

        while i < len(L) and j < len(M):
            if L[i] < M[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = M[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(M):
            arr[k] = M[j]
            j += 1
            k += 1

def print_list(arr):
    for i in range(len(arr)):
        print(arr[i], end=" ")
    print()

if __name__ == '__main__':
    array = [16, 31, 41, 39, 24, 7, 30, 11]

    print("Original array is:", end=" ")
    print_list(array)

    merge_sort(array)

    print("Sorted array is:", end=" ")
    print_list(array)

 
public class MergeSort {
    void merge(int arr[], int l, int m, int r) {
        int n1 = m - l + 1;
        int n2 = r - m;

        int L[] = new int[n1];
        int R[] = new int[n2];

        for (int i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];

        int i = 0, j = 0;

        int k = l;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    void mergeSort(int arr[], int l, int r) {
        if (l < r) {
            int m = l + (r - l) / 2;

            mergeSort(arr, l, m);
            mergeSort(arr, m + 1, r);

            merge(arr, l, m, r);
        }
    }

    void printArray(int A[]) {
        int n = A.length;
        for (int i = 0; i < n; ++i)
            System.out.print(A[i] + " ");
        System.out.println();
    }

    public static void main(String args[]) {
        MergeSort ob = new MergeSort();
        int arr[] = {16, 31, 41, 39, 24, 7, 30, 11};
        int n = arr.length;

        System.out.print("Original array is: ");
        ob.printArray(arr);

        ob.mergeSort(arr, 0, n - 1);

        System.out.print("Sorted array is: ");
        ob.printArray(arr);
    }
}

 
// Merge sort in C++

#include <iostream>
using namespace std;

// Merge two subarrays L and M into arr
void merge(int arr[], int p, int q, int r) {
  
  // Create L ← A[p..q] and M ← A[q+1..r]
  int n1 = q - p + 1;
  int n2 = r - q;

  int L[n1], M[n2];

  for (int i = 0; i < n1; i++)
    L[i] = arr[p + i];
  for (int j = 0; j < n2; j++)
    M[j] = arr[q + 1 + j];

  // Maintain current index of sub-arrays and main array
  int i, j, k;
  i = 0;
  j = 0;
  k = p;

  // Until we reach either end of either L or M, pick larger among
  // elements L and M and place them in the correct position at A[p..r]
  while (i < n1 && j < n2) {
    if (L[i] <= M[j]) {
      arr[k] = L[i];
      i++;
    } else {
      arr[k] = M[j];
      j++;
    }
    k++;
  }

  // When we run out of elements in either L or M,
  // pick up the remaining elements and put in A[p..r]
  while (i < n1) {
    arr[k] = L[i];
    i++;
    k++;
  }

  while (j < n2) {
    arr[k] = M[j];
    j++;
    k++;
  }
}

// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int l, int r) {
  if (l < r) {
    // m is the point where the array is divided into two subarrays
    int m = l + (r - l) / 2;

    mergeSort(arr, l, m);
    mergeSort(arr, m + 1, r);

    // Merge the sorted subarrays
    merge(arr, l, m, r);
  }
}

// Print the array
void printArray(int arr[], int size) {
  for (int i = 0; i < size; i++)
    cout << arr[i] << " ";
  cout << endl;
}

// Driver program
int main() {
  int arr[] = {16, 31, 41, 39, 24, 7, 30, 11};
  int size = sizeof(arr) / sizeof(arr[0]);
  cout << "Original array is: ";
      printArray(arr, size);
  mergeSort(arr, 0, size - 1);

  cout << "Sorted array is: ";
  printArray(arr, size);
  return 0;

Output

Original array is: 16 31 41 39 24 7 30 11 
Sorted array is: 7 11 16 24 30 31 39 41 

Complexity Analysis of Merge Sort Algorithm

1. Time Complexity

   Case	Time Complexity
   Best	O(n*log n)
   Worst	O(n*log n)
   Average	O(n*log n)

2. Space Complexity: We require an additional array sorted to store the final sorted array hence, the space-time complexity is O(n).

Applications of Merge Sort Algorithm

1. Sorting: As mentioned, merge sort is primarily used for sorting arrays of elements. It can efficiently sort large arrays of numbers or strings, making it a popular choice for sorting algorithms in programming.
2. External Sorting: Merge sort is also used for external sorting that involves too large data sets, difficult to fit into memory. In external sorting, the data is divided into smaller chunks that can be sorted separately and then merged.
3. Database Operations: Merge sort is used in various database operations, such as sorting data before performing a search or merging two sets of data. It is also used in indexing and for optimizing certain queries.
4. Parallel Processing: Merge sort can be used for parallel processing, which involves dividing a task into smaller parts that can be processed simultaneously. Merge sort can be divided into smaller sub-tasks that can be executed in parallel, improving overall efficiency and reducing the time for sorting.
5. Computer Graphics: Merge sort can be used for depth sorting in computer graphics, which involves determining the order in which objects should be drawn to create a 3D image. Merge sort can be used to sort the objects based on their distance from the viewer, improving the overall visual quality of the image

Advantages of Merge Sort Algorithm

1. Stable Sorting: It preserves the relative order of equal elements in the input array. This makes it useful in certain applications, such as sorting arrays of records with multiple fields.
2. Good Performance: Merge sort has a time complexity of O(nlogn), which makes it efficient for sorting large datasets. It also performs well in parallel processing environments, where multiple threads are used to sort different sub-arrays simultaneously.
3. No Worst-Case Scenario: Unlike other sorting algorithms such as quicksort, merge sort has no worst-case scenario. Its worst-case time complexity is always O(nlogn), regardless of the input data.
4. Easy to Implement: Merge sort is relatively easy to implement, even for beginners. The algorithm is based on the divide-and-conquer paradigm, which can be expressed recursively.
5. Memory Efficiency: Merge sort is a stable, in-place sorting algorithm. It can sort data without requiring extra memory space. In contrast, algorithms like quicksort require additional memory space to perform the sorting operation.

Disadvantages of Merge Sort Algorithm

1. Space Complexity: Merge Sort has a space complexity of O(n) i.e. it requires extra memory space to store the temporary sub-arrays. This can be a disadvantage if the system has limited memory resources or if the size of the input data is very large.
2. Not In-place: It requires extra memory space to store the temporary sub-arrays during the sorting process. This can be a disadvantage if the system has limited memory resources or if the size of the input data is very large.
3. Complexity: While Merge Sort has a time complexity of O(n log n), it may not be the most efficient sorting algorithm in all scenarios. For example, if the size of the input data is very small, a simpler algorithm such as insertion sort may be more efficient.
4. Recursive: Merge Sort is a recursive algorithm i.e. it calls itself repeatedly until the sorting is complete. This can lead to stack overflow errors or other performance issues if the input data is very large.
5. Not adaptive: Its performance does not change significantly based on the initial order of the input data. This can be a disadvantage in scenarios where the input data is already sorted partially or nearly sorted.

Summary

So, here we saw every aspect of the merge sort algorithm in data structures. It must have been a little difficult to understand the merge function and implement it in programming. But, not to worry. After a time, you won't find it. Just make sure you are thorough with arrays in data structures. To apply your knowledge of merge sort algorithm, enroll in our Dsa Course Free.

Similar Sorting Algorithms

• Selection Sort
• Insertion Sort
• Quick Sort
• Bucket Sort